Question
A particle moves along the
-axis so that at time t≥0 its position is given by \(y(t)=t^{3}-4t^{2}+4t+3\) .Which of the following statements describes the motion of the particle at time
?
A The particle is moving down the
-axis with decreasing velocity.
B The particle is moving down the
-axis with increasing velocity.
C The particle is moving up the
-axis with decreasing velocity.
D The particle is moving up the
-axis with increasing velocity.
▶️Answer/Explanation
Ans:A
The velocity of the particle is \(v(t)=3t^{2}-8t+4\) At time t=1, v(1)=−1. Since the velocity is negative, the particle is moving down the y-axis. The rate of change of the velocity is v′(t)=6t−8. At time t=1, v′(1)=−2. Since this is negative, the particle is moving with decreasing velocity at time t=1.
Question
For any function f, which of the following statements must be true?
I If f is defined at x = a, then .
II If f is continuous at x = a, then .
III If f is differentiable at x = a, then .
A III only
B I and II only
C II and III only
D I, II, and III
▶️Answer/Explanation
Ans:C
Question
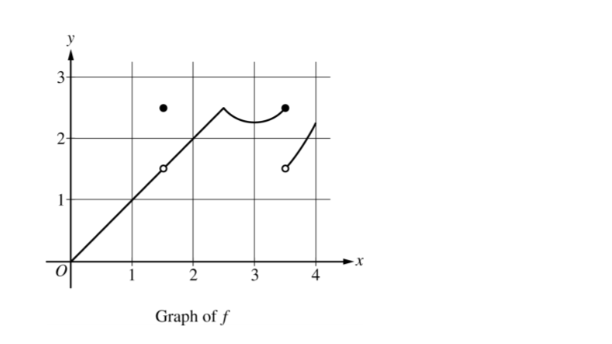
The graph of the function f is shown above. Of the following intervals, on which is f continuous but not differentiable?
A (0,1)
B (1,2)
C (2,3)
D (3,4)
▶️Answer/Explanation
Ans:C
Question
At x = 3, the function given by f(x) \(=\left\{\begin{matrix}
x^2 , x<3& \\
6x-9 , x\geq 3&
\end{matrix}\right.\) is
(A) undefined.
(B) continuous but not differentiable.
(C) differentiable but not continuous.
(D) neither continuous nor differentiable.
(E) both continuous and differentiable.
▶️Answer/Explanation
Ans:E
The function is continuous at \(x=3 since \lim_{x\rightarrow 3^-}f(x)=\lim_{x\rightarrow 3^+}f(x)=9=f(3)\). Also, the derivative as you approach x = 3 from the left is 6 and the derivative as you approach x = 3 from the right is also 6. These two facts imply that f is differentiable at x = 3. The function is clearly continuous and differentiable at all other values of x.
