AP Calculus BC 1.3 Estimating Limit Values from Graphs - MCQs - Exam Style Questions
Question
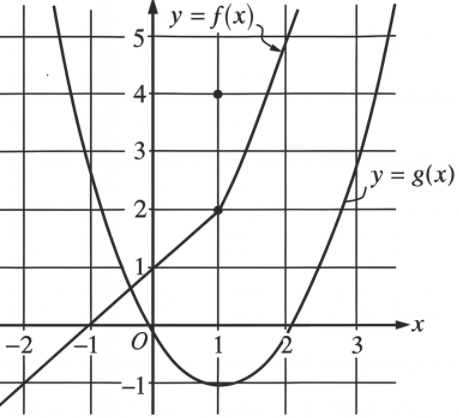
The graphs of \(f\) and \(g\) are shown. The function \(f\) has a removable discontinuity, and \(g\) is continuous. What is \( \displaystyle \lim_{x\to 1}\frac{f(x)}{g(x)} \)?
(A) \(-4\)
(B) \(-2\)
(C) \(-\tfrac{1}{2}\)
(D) Nonexistent
(B) \(-2\)
(C) \(-\tfrac{1}{2}\)
(D) Nonexistent
▶️ Answer/Explanation
From the graph near \(x=1\): \(\displaystyle \lim_{x\to 1} f(x)=2\) (hole at \(y=2\)), and \(g\) is continuous with \(g(1)=-1\).
Thus \[ \lim_{x\to 1}\frac{f(x)}{g(x)} = \frac{\lim_{x\to 1} f(x)}{\lim_{x\to 1} g(x)} = \frac{2}{-1} = -2. \] ✅ Answer: (B)
Thus \[ \lim_{x\to 1}\frac{f(x)}{g(x)} = \frac{\lim_{x\to 1} f(x)}{\lim_{x\to 1} g(x)} = \frac{2}{-1} = -2. \] ✅ Answer: (B)
