Question
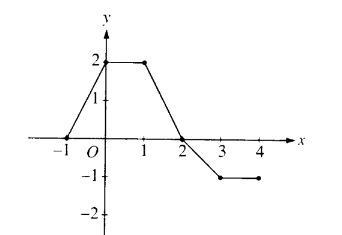
The graph of a piecewise-linear function f , for \(−1 ≤ x ≤4 \), is shown above. What is the value of \(\int_{-1}^{4}f(x)dx\)?
(A) 1 (B) 2.5 (C) 4 (D) 5.5 (E) 8
▶️Answer/Explanation
Ans:B
\(\int_{-1}^{4}f(x)dx=\int_{-1}^{2}f(x)dx+\int_{2}^{4}f(x)dx\)
= Area of trapezoid(1) – Area of trapezoid(2) = 4 -1.5= 2.5
▶️ Answer/Explanation
Solution
Substitute \( u = \sqrt{x} \), so \( x = u^2 \) and \( dx = 2u \, du \).
Integral becomes: \(\int \frac{e^u}{u} \cdot 2u \, du = \int 2e^u \, du\).
Integrate: \( 2 \int e^u \, du = 2e^u + C \).
Substitute back \( u = \sqrt{x} \): \( 2e^{\sqrt{x}} + C \).
✅ Answer: A
▶️ Answer/Explanation
Solution
By the Fundamental Theorem of Calculus, if \( f(x) = \int_{a}^{x} g(t) \, dt \), then \( f'(x) = g(x) \).
Here, \( f(x) = \int_{1}^{x} \frac{1}{t} \, dt \), so \( f'(x) = \frac{1}{x} \).
✅ Answer: B
▶️ Answer/Explanation
Solution
By the Fundamental Theorem of Calculus, \(\frac{d}{dx} \int_{a}^{x} f(u) \, du = f(x)\).
Here, \(\frac{d}{dx} \int_{0}^{x} \cos(2\pi u) \, du = \cos(2\pi x)\).
✅ Answer: D