AP Calculus BC 6.13 Evaluating Improper Integrals - FRQs - Exam Style Questions
Calc-Ok Question
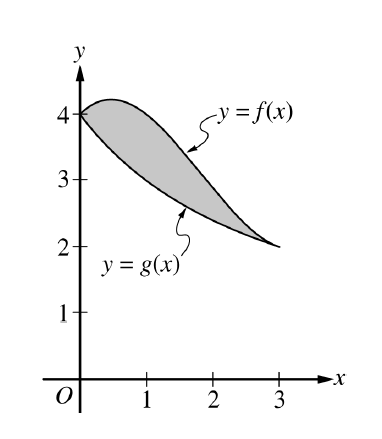
The graphs of functions \(f\) and \(g\) are shown for \(0 \le x \le 3\). It is known that \(g(x)=\dfrac{12}{3+x}\) for \(x\ge 0\). The twice-differentiable function \(f\) (not given explicitly) satisfies \(f(3)=2\) and \(\displaystyle \int_{0}^{3} f(x)\,dx = 10\).
(a) Find the area of the shaded region enclosed by the graphs of \(f\) and \(g\).
(b) Evaluate the improper integral \(\displaystyle \int_{0}^{\infty} (g(x))^{2}\,dx\), or show that the integral diverges.
(c) Let \(h\) be defined by \(h(x)=x\,f'(x)\). Find the value of \(\displaystyle \int_{0}^{3} h(x)\,dx\).
Most-appropriate topic codes:
• TOPIC 8.4: Area Between Curves (functions of x) — part (a)
• TOPIC 6.13: Improper Integrals (BC) — part (b)
• TOPIC 6.11: Integration by Parts (definite form, BC) — part (c)
• TOPIC 6.13: Improper Integrals (BC) — part (b)
• TOPIC 6.11: Integration by Parts (definite form, BC) — part (c)
▶️ Answer/Explanation
(a) Area between \(f\) and \(g\)
On \([0,3]\), shaded area \[ A = \int_{0}^{3}\!\big(f(x)-g(x)\big)\,dx = \int_{0}^{3}\!f(x)\,dx – \int_{0}^{3}\!g(x)\,dx. \] Given \(\int_{0}^{3} f(x)\,dx = 10\). Compute \(\displaystyle \int_{0}^{3} g(x)\,dx = \int_{0}^{3} \frac{12}{3+x}\,dx = 12[\ln(3+x)]_{0}^{3} = 12(\ln 6-\ln 3) = 12\ln 2.\) Hence \(\boxed{A = 10 – 12\ln 2}.\)(b) Improper integral
\[ \int_{0}^{\infty} (g(x))^{2}dx = \lim_{b\to\infty} \int_{0}^{b} \frac{144}{(3+x)^{2}}\,dx = \lim_{b\to\infty}\Big[-\frac{144}{3+x}\Big]_{0}^{b} = \lim_{b\to\infty}\Big(48 – \frac{144}{3+b}\Big) = \boxed{48}. \](c) \(\displaystyle \int_{0}^{3} h(x)\,dx\) with \(h(x)=x\,f'(x)\)
Integration by parts: \(u=x\Rightarrow du=dx\), \(dv=f'(x)dx\Rightarrow v=f(x)\). \[ \int x f'(x)\,dx = x f(x) – \int f(x)\,dx. \] Evaluate from \(0\) to \(3\): \[ \int_{0}^{3} h(x)\,dx = [x f(x)]_{0}^{3} – \int_{0}^{3} f(x)\,dx = 3f(3) – 10 = 3\cdot 2 – 10 = \boxed{-4}. \]