AP Calculus AB 6.14 Selecting Techniques for Antidifferentiation - MCQs - Exam Style Questions
No-Calc Question
(A) \(2e^{\sqrt{x}}+C\)
(B) \(\tfrac{1}{2}e^{\sqrt{x}}+C\)
(C) \(e^{\sqrt{x}}+C\)
(D) \(2\sqrt{x}\,\times e^{\sqrt{x}}+C\)
(E) \(\tfrac{1}{2}\,\dfrac{e^{\sqrt{x}}}{\sqrt{x}}+C\)
▶️ Answer/Explanation
Let \(u=\sqrt{x}\Rightarrow du=\dfrac{1}{2\sqrt{x}}\,dx\).
Then \(dx=2\sqrt{x}\,du\). Substitute into the integral:
\(\displaystyle \int \frac{e^{\sqrt{x}}}{\sqrt{x}}\,dx=\int \frac{e^{u}}{u}\,\bigl(2u\,du\bigr)=\int 2\times e^{u}\,du=2\times e^{u}+C=2e^{\sqrt{x}}+C\).
Answer: (A)
No-Calc Question
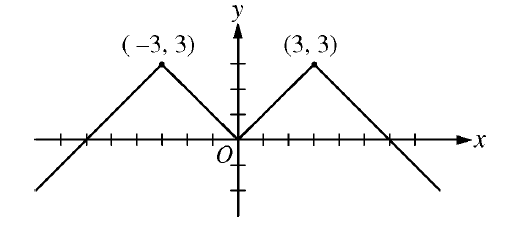
The graph of the even function \(y=f(x)\) consists of 4 line segments, as shown above. Which of the following statements about \(f\) is false?
(A) \(\displaystyle \lim_{x\to 0}\bigl(f(x)-f(0)\bigr)=0\)
(B) \(\displaystyle \lim_{x\to 0}\frac{f(x)-f(0)}{x}=0\)
(C) \(\displaystyle \lim_{x\to 0}\frac{f(x)-f(-x)}{2x}=0\)
(D) \(\displaystyle \lim_{x\to 2}\frac{f(x)-f(2)}{x-2}=1\)
(E) \(\displaystyle \lim_{x\to 3}\frac{f(x)-f(3)}{x-3}\) does not exist.
▶️ Answer/Explanation
From the piecewise-linear even graph, near \(x=0\) we have \(f(x)=|x|\) and \(f(0)=0\).
(A) \(\lim_{x\to 0}(f(x)-f(0))=\lim_{x\to 0}|x|=0\) — true.
(B) \(\lim_{x\to 0}\dfrac{f(x)-f(0)}{x}=\lim_{x\to 0}\dfrac{|x|}{x}\) has right-hand limit \(+1\) and left-hand limit \(-1\), so it does not exist (not \(0\)) — false.
(C) \(f\) is even, so \(f(x)=f(-x)\Rightarrow\) numerator \(=0\) for \(x\ne 0\); the limit is \(0\) — true.
(D) On the segment containing \(x=2\) the slope is \(1\), so the limit of the difference quotient equals \(1\) — true.
(E) At \(x=3\) the graph has a corner, so the derivative limit does not exist — true.
Answer: (B)
