AP Calculus BC 6.5 Interpreting the Behavior of Accumulation Functions Involving Area - FRQs - Exam Style Questions
No-Calc Question
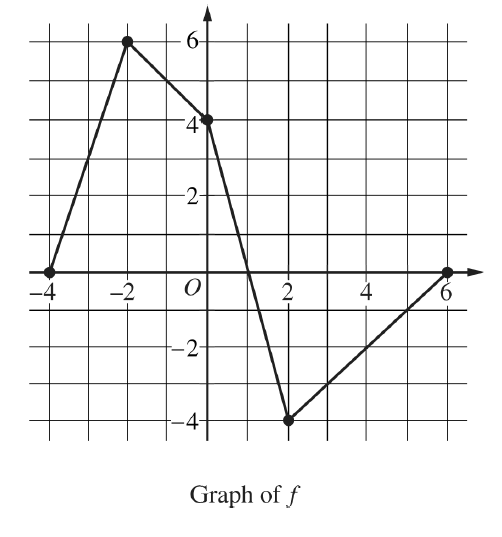
Let \(f\) be continuous on \([\,-4,\,6\,]\). The graph of \(f\) (four line segments) is shown. Define \( \displaystyle G(x)=\int_{0}^{x} f(t)\,dt \).
(a) On what open intervals is the graph of \(G\) concave up? Give a reason.
(b) Let \(P(x)=G(x)\,f(x)\). Find \(P'(3)\).
(c) Find \( \displaystyle \lim_{x\to 2}\frac{G(x)}{x^{2}-2x} \).
(d) Find the average rate of change of \(G\) on \([\,-4,\,2\,]\). Does the Mean Value Theorem guarantee a value \(c\) with \(-4<c<2\) such that \(G'(c)\) equals this average rate? Justify.
Most-appropriate topic codes (CED):
• TOPIC \(5.6\): Determining Concavity of Functions over Intervals — part (a)
• TOPIC \(2.8\): Product Rule — part (b)
• TOPIC \(6.5\): Interpreting Accumulation Functions \((G'(x)=f(x))\) — parts (b), (c), (d)
• TOPIC \(4.7\): L’Hospital’s Rule — part (c)
• TOPIC \(5.1\): Mean Value Theorem — part (d)
• TOPIC \(2.8\): Product Rule — part (b)
• TOPIC \(6.5\): Interpreting Accumulation Functions \((G'(x)=f(x))\) — parts (b), (c), (d)
• TOPIC \(4.7\): L’Hospital’s Rule — part (c)
• TOPIC \(5.1\): Mean Value Theorem — part (d)
▶️ Answer/Explanation
(a) Concavity of \(G\)
\(G'(x)=f(x)\) and \(G”(x)=f'(x)\).
\(G\) is concave up where \(f'(x)>0\) (i.e., where \(f\) increases).
From the graph, \(f\) increases on \((\,-4,\,-2\,)\) and \((\,2,\,6\,)\).
\(\boxed{\text{Therefore, }G\text{ is concave up on }(\,-4,\,-2\,)\text{ and }(\,2,\,6\,).}\)
(b) \(P'(3)\)
\(P(x)=G(x)\,f(x)\Rightarrow P'(x)=G'(x)f(x)+G(x)f'(x)=f(x)^{2}+G(x)f'(x)\).
On \([\,2,6\,]\), \(f(x)=x-6\Rightarrow f(3)=-3,\ f'(3)=1\).
\(G(3)=\displaystyle\int_{0}^{3}f(t)\,dt=\int_{0}^{2}f(t)\,dt+\int_{2}^{3}(t-6)\,dt\).
\(\int_{0}^{2}f(t)\,dt=0\) (net area \(=0\)); \(\ \int_{2}^{3}(t-6)\,dt=\big[\tfrac12 t^{2}-6t\big]_{2}^{3}=-\tfrac{7}{2}\).
Hence \(G(3)=-\tfrac{7}{2}\).
\(P'(3)=(-3)^{2}+(-\tfrac{7}{2})(1)=9-\tfrac{7}{2}=\boxed{\tfrac{11}{2}}.\)
(c) Limit
\(G(2)=\displaystyle\int_{0}^{2}f(t)\,dt=0\) and \(x^{2}-2x\to 0\) as \(x\to 2\Rightarrow\) form \(0/0\).
By L’Hospital’s Rule, \[ \lim_{x\to 2}\frac{G(x)}{x^{2}-2x} =\lim_{x\to 2}\frac{G'(x)}{2x-2} =\lim_{x\to 2}\frac{f(x)}{2x-2} =\frac{f(2)}{2}. \] From the graph, \(f(2)=-4\). Thus the limit is \(\boxed{-2}\).
(d) Average rate of change and MVT
\(\displaystyle \int_{-4}^{0} f(t)\,dt=\text{(triangle area)}+\text{(trapezoid area)} =\tfrac12\cdot 2\cdot 6+\tfrac12(6+4)\cdot 2=6+10=16.\)
Hence \(G(-4)=\displaystyle\int_{0}^{-4} f(t)\,dt=-16\) and \(G(2)=0\).
Average rate on \([\,-4,\,2\,]\): \[ \frac{G(2)-G(-4)}{2-(-4)}=\frac{0-(-16)}{6}=\frac{16}{6}=\boxed{\tfrac{8}{3}}. \] Since \(f\) is continuous on \([\,-4,2\,]\), \(G\) is differentiable on \((\,-4,2\,)\) and continuous on \([\,-4,2\,]\).
By the Mean Value Theorem, there exists \(c\) with \(-4<c<2\) such that \(G'(c)=\tfrac{8}{3}\).
But \(G'(c)=f(c)\). Therefore \(\boxed{f(c)=\tfrac{8}{3}}\) for some \(-4<c<2\).
\(G'(x)=f(x)\) and \(G”(x)=f'(x)\).
\(G\) is concave up where \(f'(x)>0\) (i.e., where \(f\) increases).
From the graph, \(f\) increases on \((\,-4,\,-2\,)\) and \((\,2,\,6\,)\).
\(\boxed{\text{Therefore, }G\text{ is concave up on }(\,-4,\,-2\,)\text{ and }(\,2,\,6\,).}\)
(b) \(P'(3)\)
\(P(x)=G(x)\,f(x)\Rightarrow P'(x)=G'(x)f(x)+G(x)f'(x)=f(x)^{2}+G(x)f'(x)\).
On \([\,2,6\,]\), \(f(x)=x-6\Rightarrow f(3)=-3,\ f'(3)=1\).
\(G(3)=\displaystyle\int_{0}^{3}f(t)\,dt=\int_{0}^{2}f(t)\,dt+\int_{2}^{3}(t-6)\,dt\).
\(\int_{0}^{2}f(t)\,dt=0\) (net area \(=0\)); \(\ \int_{2}^{3}(t-6)\,dt=\big[\tfrac12 t^{2}-6t\big]_{2}^{3}=-\tfrac{7}{2}\).
Hence \(G(3)=-\tfrac{7}{2}\).
\(P'(3)=(-3)^{2}+(-\tfrac{7}{2})(1)=9-\tfrac{7}{2}=\boxed{\tfrac{11}{2}}.\)
(c) Limit
\(G(2)=\displaystyle\int_{0}^{2}f(t)\,dt=0\) and \(x^{2}-2x\to 0\) as \(x\to 2\Rightarrow\) form \(0/0\).
By L’Hospital’s Rule, \[ \lim_{x\to 2}\frac{G(x)}{x^{2}-2x} =\lim_{x\to 2}\frac{G'(x)}{2x-2} =\lim_{x\to 2}\frac{f(x)}{2x-2} =\frac{f(2)}{2}. \] From the graph, \(f(2)=-4\). Thus the limit is \(\boxed{-2}\).
(d) Average rate of change and MVT
\(\displaystyle \int_{-4}^{0} f(t)\,dt=\text{(triangle area)}+\text{(trapezoid area)} =\tfrac12\cdot 2\cdot 6+\tfrac12(6+4)\cdot 2=6+10=16.\)
Hence \(G(-4)=\displaystyle\int_{0}^{-4} f(t)\,dt=-16\) and \(G(2)=0\).
Average rate on \([\,-4,\,2\,]\): \[ \frac{G(2)-G(-4)}{2-(-4)}=\frac{0-(-16)}{6}=\frac{16}{6}=\boxed{\tfrac{8}{3}}. \] Since \(f\) is continuous on \([\,-4,2\,]\), \(G\) is differentiable on \((\,-4,2\,)\) and continuous on \([\,-4,2\,]\).
By the Mean Value Theorem, there exists \(c\) with \(-4<c<2\) such that \(G'(c)=\tfrac{8}{3}\).
But \(G'(c)=f(c)\). Therefore \(\boxed{f(c)=\tfrac{8}{3}}\) for some \(-4<c<2\).
