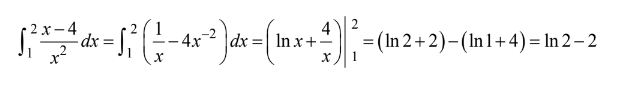Question
If \(\begin{Bmatrix}
f(x)=8-x^{2} for -2\leq x\leq 2 & then \int_{-1}^{3} & \\
f(x)=x^{2} & elsewhere, &
\end{Bmatrix} \) f(x) is a number between
(A) 0 and 8 (B) 8 and 16 (C) 16 and 24 (D) 24 and 32 (E) 32 and 40
▶️Answer/Explanation
Ans:D
\(\int_{-1}^{3}f(x)dx= \int_{-1}^{2}(8-x^{2})dx+\int_{2}^{3}x^{2}dx=\left ( 8x-\frac{1}{3}x^{3} \right )\)
Question
If F and f are continuous functions such that F'(x ) =F(x for all x, then \(\int_{a}^{b}f(x) dx\) is
(A) F'(a )- f’ ( b)
(B) F'(b )- F'(a )
(C) F(a)- F(b)
(D) F(b )-F’ (a )
(E) none of the above
▶️Answer/Explanation
Ans:D
By the Fundamental Theorem of Calculus,\(\int_{a}^{b}f(x)dx=F(b)-F(a) where F'(x)=f'(x)\).
Question
\(\int_{0}^{\pi /4} tan^{2}dx\)=
(A)\(\frac{\pi }{4}-1\) (B)\( 1-\frac{\pi }{4}\) (C) \(\frac{1}{3}\) (D)\(\sqrt{2}-1\) (E)\(\frac{\pi }{4}+1\)
▶️Answer/Explanation
Ans:B
\(\int_{0}^{\pi/4}tan^2xdx =\int_{0}^{\pi/4}(sec^2x-1)dx=(tanx-x)|_{0}^{\pi/4}=1-\frac{\pi}{4}\)
Question
\(\int_{1}^{2} \frac{x-4}{x^{2}}dx\)=
(A)\(-\frac{1}{2}\) (B) In2-2 (C) In2 (D) 2 (E) In2+2
▶️Answer/Explanation
Ans:B