Question
\(\int_{\pi /4}^{\pi /2}\frac{cosx}{sinx}dx\)=
(A)In\(\sqrt{2} \) (B)In\(\frac{\pi }{4} \) (C)In\(\sqrt{3}\) (D)In\(\frac{\sqrt{3}}{2}\) (E)Ine
▶️Answer/Explanation
Ans:A
Question
\(\int \frac{5}{1+x^{2}}dx\)=
(A)\(\frac{-10x}{(1+x^{2})^{2}}+C\) (B) \(\frac{5}{2x}In (1+x^{2})+C\) (C)\(5x-\frac{5}{x}+C\) (D)\(5arctanx+C\) (E)\(5In(1+x^{2})+C\)
▶️Answer/Explanation
Ans:D
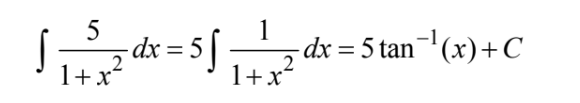
Question
If \(\frac{dy}{dx} =tanx\),then y=
(A)\(\frac{1}{2}tan^{2}x+C\) (B)\(sec^{2}x+C\) (C)\(In|secx|+c \) (D) In|cosx|+C (E) secxtanx+C
▶️Answer/Explanation
Ans:C
\(\int tanx dx=\int \frac{sinx}{cosx}dx=-ln|cosx|+C=ln |secx|+C\)
Question
\(\int_{\pi /4}^{\pi /2}\frac{cosx}{sinx}dx\)=
(A)In\(\sqrt{2} \) (B)In\(\frac{\pi }{4} \) (C)In\(\sqrt{3}\) (D)In\(\frac{\sqrt{3}}{2}\) (E)Ine
▶️Answer/Explanation
Ans:A
\(\int_{\pi/4}^{\pi/2}\frac{cosx}{sinx}dx=ln (sinx)|_{\pi/4}^{\pi/2}=ln 1-ln\frac{1}{\sqrt{2}}=ln\sqrt{2}\)
Question
\(\int sin(2x+3)dx=\)
(A)\(\frac{1}{2}cos(2x+3)+c\) (B)\((cos(2x+x)+C \) (C)\(-cos(2x+3)+C\) (D)\(-\frac{1}{2}cos(2x+3)+C\) (E)\(-\frac{1}{5}cos(2x+3)+C\)
▶️Answer/Explanation
Ans:D
\( \int sin (2x+3)dx=-\frac{1}{2}cos(2x+3)+C\)
