Question
During a certain epidemic, the number of people that are infected at any time increases at a rate proportional to the number of people that are infected at that time. If 1,000 people are infected when the epidemic is first discovered, and 1,200 are infected 7 days later, how many people are infected 12 days after the epidemic is first discovered?
(A) 343 (B) 1,343 (C) 1,367 (D) 1,400 (E) 2,057
▶️Answer/Explanation
Ans:C
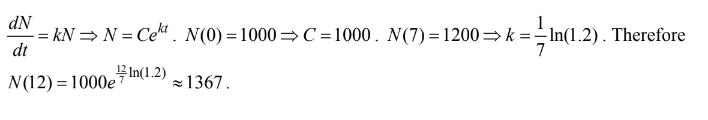
Question
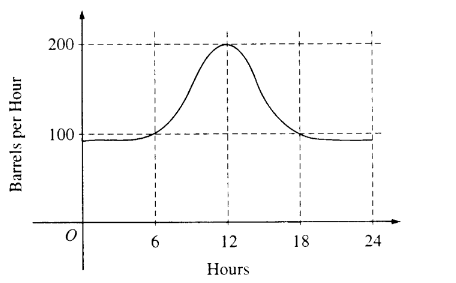
The flow of oil, in barrels per hour, through a pipeline on July 9 is given by the graph shown above. Of the following, which best approximates the total number of barrels of oil that passed through the pipeline that day?
(A) 500 (B) 600 (C) 2,400 (D) 3,000 (E) 4,800
▶️Answer/Explanation
Ans:D
Let r(t) be the rate of oil flow as given by the graph, where t is measured in hours. The total number of barrels is given by \(\int_{0}^{24}r(t)dt\). This can be approximated by counting the squares below the curve and above the horizontal axis. There are approximately five squares with area 600 barrels. Thus the total is about 3,000 barrels.
Question
John Hersey High School, which has 1,532 students, is circulating a rumor that 3rd period on Friday will be canceled for a fire drill. On Monday, 7 people have heard the rumor. On Tuesday, 84 people have heard the rumor. How many people will have heard the rumor by Thursday?
(A) 1,384 students
(B) 1,178 students
(C) 785 students
(D) 598 students
▶️Answer/Explanation
Ans:(A)

Question
A college dorm that houses 300 students experiences an outbreak of measles. The Health Center recognizes the outbreak when 4 students are diagnosed on the same day. Residents are quarantined to restrict this infection to one building. After 7 days, 17 students are sick with measles. Use a logistic model to describe the course of the infection and predict the number of students infected after 14 days.
(A) 34 students
(B) 44 students
(C) 54 students
(D) 64 student
▶️Answer/Explanation
Ans: (D)
Recall the following equations for logistic models:
\(\frac{\mathrm{d} P}{\mathrm{d} t}=kP\left ( 1-\frac{P}{K} \right ),P(t)=\frac{K}{Ae^{-kt}+1},A=\frac{K-P_{0}}{P_{0}}\)
Let t = the number of days after the first diagnosis. From the problem you see that K = 300, P(0)=4, P(7)=17.
\(A=\frac{KI-P_{0}}{P_{0}}=\frac{300-4}{4}=74\)
\(P(t)=\frac{K}{Ae^{-kt}+1}=\frac{300}{74e^{-kt}+1}\)
You can use the information that P(7) = 17 to solve for k.
\(17=\frac{300}{74e^{-k(7)}+1}\Rightarrow 74e^{-7k}+1=\frac{300}{17}\Rightarrow e^{-7k}\approx 0.225\Rightarrow \ln (e^{-7k})=\ln (0.225)\)
\(-7k\approx -1.49\Rightarrow k\approx 0.213\)
To estimate the number of students infected after 2 weeks, you evaluate
\(P(14)=\frac{300}{74e^{-(0.213)(14)}+1}\approx 63.1\)
