Question
If \(\frac{dy}{dx}=2y^{2}\) and if y=-1 , when x = 1, then when x = 2, y =
(A) \(-\frac{2}{3}\) (B) \(−\frac{1}{3}\) (C) 0 (D) \(\frac{1}{3}\) (E)\(\frac{2}{3}\)
▶️Answer/Explanation
Ans:B
Question
Population y grows according to the equation \(\frac{dy}{dt}=ky\) , where k is a constant and t is measured in years. If the population doubles every 10 years, then the value of k is
(A) 0.069 (B) 0.200 (C) 0.301 (D) 3.322 (E) 5.000
▶️Answer/Explanation
Ans:A
A known solution to this differential equation is \(y(t) = y(0)et^{kt}\). Use the fact that the population is 2y(0) when t=10. Then\( 2y(0) = y(0)e^{k(10)} ⇒ e^{10k} = 2⇒ k = (0.1) In 2= 0.069\)
Question
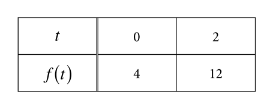
Let be a solution to the differential equation \(\frac{dy}{dt}=ky\) where k is a constant. Values of f for selected values of t are given in the table above. Which of the following is an expression for f(t)?
(A) \(4e^{\frac{t}{2}ln3}\)
(B) \(e^{\frac{t}{2}ln9}+3\)
(C)\(2t^{2}+4\)
(D) \(4t+4\)
▶️Answer/Explanation
Ans:A
Question
If \(\frac{dy}{dx}=ysec^{2}x\)
(A)\(e^{tanx}+4 \) (B)\(e^{tanx}+5\) (C)\(5e^{tanx}\) (D)\(tanx+5\) (E)\(tanx+5e^{x}\)
▶️Answer/Explanation
Ans:C
\(\frac{dy}{y} =sec^2xdx=ln|y|=tanx+k=y=Cetanx y(0)=5⇒y=5e^{tan}\)
