Question
The number of bacteria in a culture is growing at a rate of per unit of time t. At t = 0 , the number of bacteria present was 7,500. Find the number present at t = 5 .
(A) \(1, 200e ^{2}\) (B) \(3,000e^{2}\) (C) \(7,500e^{2}\) (D) 57,500e (E) \(\frac{15,000}{7}e^{7}\)
▶️Answer/Explanation
Ans:C
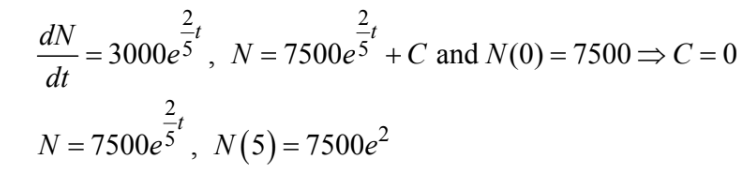
Question
The number of bacteria in a culture is growing at a rate of\(3,000e^{2t/5}\) per unit of time t. At t = 0 , the number of bacteria present was 7,500. Find the number present at t = 5 .
(A) \(1, 200e^{2}\) (B) \(3,000e^{2}\) (C) \(7,500e^{2}\) (D)\( 7,500e^{5}\) (E)\(\frac{15,000}{7}e^{7}\)
▶️Answer/Explanation
Ans:C
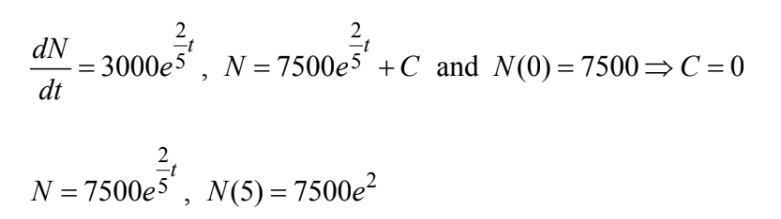
Question
\(f'(x) and f(1)=1\) ,then f(x)
(A)\(\frac{1}{2}e^{-2x+2}\) (B)\(e^{-x-1}\) (C)\(e^{1-x}\) (D)\(e^{-x} -e^{x}\)
▶️Answer/Explanation
Ans:C
\(\frac{dy}{dx}=-y\Rightarrow y=ce^{-x}\) and \(1= ce^{-1}\Rightarrow c=e;y=e.e^{-x}=e^{1-x}\)
Question
Plutonium has a half-life of 8,645 years. Using your calculator, if there are initially 20 g of plutonium, how many grams are left after 1,000 years?
(A) ≈ 45
(B) ≈ 18
(C) ≈ 35
(D) ≈ 15
▶️Answer/Explanation
Ans:(B)
Recall the equation for exponential growth/decay is
\(y=y_{0}e^{kt}\)
Since the half-life is 8645 years and you start with 20 g
\(\Rightarrow 10=20e^{(k)(8645)}\)
\(\Rightarrow \frac{1}{2}=e^{8645k}\)
To solve the exponential equation for k you take the natural log of both sides.
\(\Rightarrow \ln \left ( \frac{1}{2} \right )=\ln (e^{8645k})\)
\(\Rightarrow \ln (1)-\ln (2)=(8645k)(ln(e))\)
Now recall that ln(1) = 0 and ln(e) = 1.
\(\Rightarrow -\ln (2)=8645k\Rightarrow k=-\frac{\ln (2)}{8645}\Rightarrow y=20e^{-\frac{\ln (2)}{8645}t}\)
Now to find how many grams are left after 1,000 years, you can plug t = 1,000 into the equation
\(y=20e^{\frac{-\ln (2)}{8645}(1,000)}\approx 18\)
