Question
Let D represent the region bounded by the unit circle centered at the origin. Find the volume of the solid obtained by revolving D about the line x = 2.
(A)\(\frac{8\pi }{3}+4\pi ^{2}\)
(B) \(\frac{2\pi }{3}+\pi ^{2}\)
(C) \(\pi \left ( \frac{4}{3} +\sqrt{2}\right )\)
(D) \(\frac{8\pi }{3}\)
▶️Answer/Explanation
Ans:(A)

Question
What is the volume of the solid generated by rotating about y = -1 the region in the first quadrant bounded by the curves y = 3 – x and \(y=\frac{x}{2}\) ?
(A) \(\frac{7\pi }{3}\)
(B) \(\pi \left [ \frac{7}{3} -\pi \ln 4\right ]\)
(C) \(\pi \left [ \frac{9}{2}+\ln 3 \right ]\)
(D) \(\pi \left [ \frac{10}{3}-4\ln 2 \right ]\)
▶️Answer/Explanation
Ans:(D)

Question
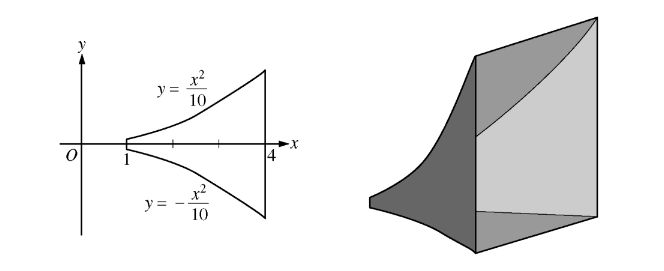
The base of a loudspeaker is determined by the two curves \(y=\frac{x^{2}}{10} \)and \(y=-\frac{x^{2}}{10} for 1\leq x\leq 4,\) as shown in
the figure above. For this loudspeaker, the cross sections perpendicular to the x-axis are squares. What is the volume of the loudspeaker, in cubic units?
(A) 2.046 (B) 4.092 (C) 4.200 (D) 8.184 (E) 25.711
▶️Answer/Explanation
Ans:D
Question
Let a > 0, and consider the solid S obtained by revolving about the y-axis the region bounded by the curve y = x, the x-axis, and the line x = a. If the volume of S is known to be 18p, find a.
(A) 1
(B) \(\frac{3}{2}\)
(C) 2
(D) 3
▶️Answer/Explanation
Ans:(D)
Each cross section perpendicular to the y-axis is a washer of area \(A(y)=\pi (a^{2}-y^{2})\)
The volume may be computed in terms of a:
\(\pi \int_{0}^{a}(a^{2}-y^{2})dy=\pi \left [ a^{2}y- \frac{y^{3}}{3}\right ]^{a}_{0}=\pi \left ( a^{3}-\frac{a^{3}}{3} \right )=\frac{2\pi a^{3}}{3}.\)
Thus, you solve \(18\pi =\frac{2\pi a^{3}}{3}\) for a,to obtain a=3.
