AP Calculus BC 8.9 Volume with Disc Method: Revolving Around the x- or y-Axis - FRQs - Exam Style Questions
No-Calc Question
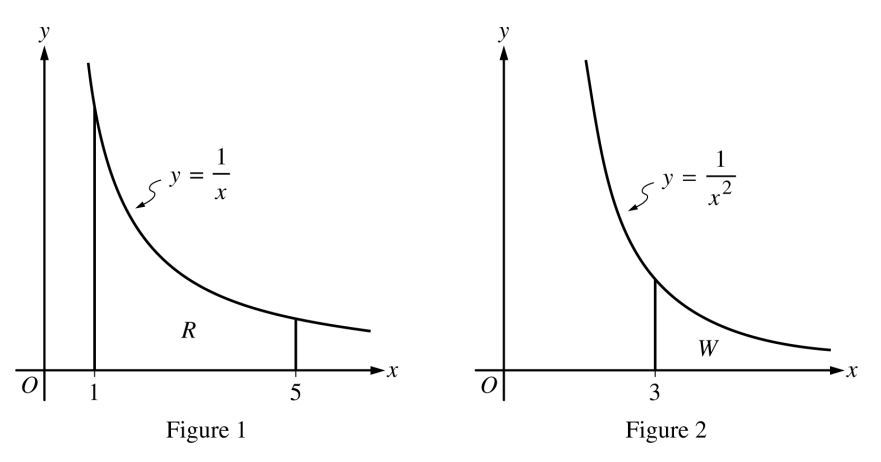
Figures 1 and 2, shown above, illustrate regions in the first quadrant associated with the graphs of \(y=\tfrac{1}{x}\) and \(y=\tfrac{1}{x^{2}}\), respectively. In Figure 1, let \(R\) be the region bounded by the graph of \(y=\tfrac{1}{x}\), the \(x\)-axis, and the vertical lines \(x=1\) and \(x=5\). In Figure 2, let \(W\) be the unbounded region between the graph of \(y=\tfrac{1}{x^{2}}\) and the \(x\)-axis that lies to the right of the vertical line \(x=3\).
Most-appropriate topic codes (CED):
• TOPIC 8.7: Volumes with Cross Sections: Squares and Rectangles — part (b)
• TOPIC 8.9: Volume with Disc Method: Revolving Around the \(x\)- or \(y\)-Axis — part (c)
▶️ Answer/Explanation
(a)
Area of \(R\) (curve above the \(x\)-axis):
\[ \text{Area}=\int_{1}^{5}\frac{1}{x}\,dx =\big[\ln x\big]_{1}^{5} =\ln 5. \]
(b)
Cross-sectional area \(A(x)=x e^{x/5}\).
Volume: \[ V=\int_{1}^{5} x e^{x/5}\,dx. \] Integration by parts:
\(u=x,\ dv=e^{x/5}dx \Rightarrow du=dx,\ v=5e^{x/5}\).
\[ \int x e^{x/5}dx = x\cdot 5e^{x/5}-\int 5e^{x/5}dx = 5x e^{x/5}-25 e^{x/5}+C = 5e^{x/5}(x-5)+C. \] Evaluate on \([1,5]\):
\[ V=\Big[5e^{x/5}(x-5)\Big]_{1}^{5} = 5e^{1}(5-5)\;-\;5e^{1/5}(1-5) = 0 – \big(-20e^{1/5}\big) = 20e^{1/5}\ \text{(cubic units)}. \]
(c)
Revolve \(W\) about the \(x\)-axis (disc method). Radius \(=y=\tfrac{1}{x^{2}}\).
\[ V=\pi\int_{3}^{\infty}\!\left(\frac{1}{x^{2}}\right)^{2}dx =\pi\int_{3}^{\infty}\frac{1}{x^{4}}\,dx =\pi\lim_{b\to\infty}\int_{3}^{b}x^{-4}dx. \] Antiderivative and limit:
\[ \int x^{-4}dx=\frac{x^{-3}}{-3}=-\frac{1}{3x^{3}},\quad V=\pi\lim_{b\to\infty}\left[-\frac{1}{3x^{3}}\right]_{3}^{b} =\pi\left(0+\frac{1}{3\cdot 3^{3}}\right) =\frac{\pi}{81}\ \text{(cubic units)}. \]
