AP Calculus BC 9.9 Finding the Area of the Region Bounded by Two Polar Curves - MCQs - Exam Style Questions
Calc-Ok Question
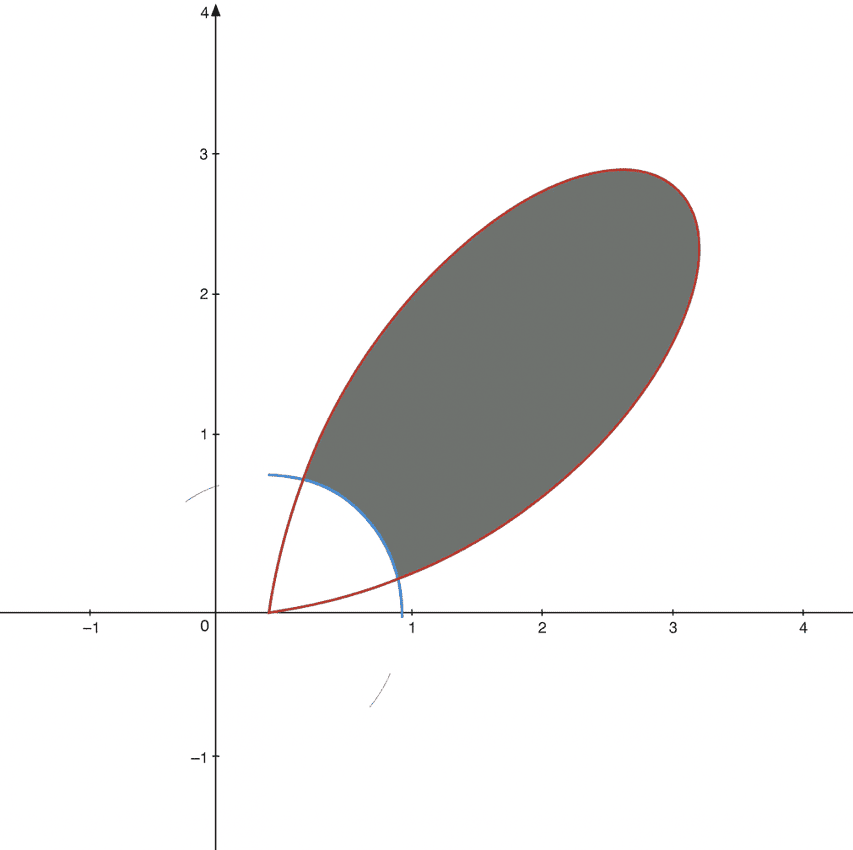
The figure shows the polar curves \(r=4(\sin 2\theta)^{2}\) and \(r=1\) for \(0\le\theta\le \tfrac{\pi}{2}\). What is the area of the shaded region?
(B) \(4.134\)
(C) \(3.927\)
(D) \(1.913\)
▶️ Answer/Explanation
Intersection with \(r=1\): \(4\sin^{2}(2\theta)=1\Rightarrow \sin(2\theta)=\tfrac12\) (since \(0\le2\theta\le\pi\)).
Thus \(\theta=\tfrac{\pi}{12}\) and \(\theta=\tfrac{5\pi}{12}\). On this interval \(r_{\text{outer}}=4\sin^{2}(2\theta)\ge1=r_{\text{inner}}\).
Area between polar curves:
\(\displaystyle A=\int_{\pi/12}^{5\pi/12}\frac12\big(r_{\text{outer}}^{2}-r_{\text{inner}}^{2}\big)\,d\theta =\int_{\pi/12}^{5\pi/12}\!\Big(8\sin^{4}(2\theta)-\tfrac12\Big)d\theta.\)
Use \(\sin^{4}x=\tfrac{3}{8}-\tfrac12\cos(2x)+\tfrac18\cos(4x)\) with \(x=2\theta\):
\(\displaystyle \int \sin^{4}(2\theta)d\theta =\tfrac{3}{8}\theta-\tfrac{1}{8}\sin(4\theta)+\tfrac{1}{64}\sin(8\theta).\)
So
\(\displaystyle A=\Big[3\theta-\sin(4\theta)+\tfrac18\sin(8\theta)\Big]_{\pi/12}^{5\pi/12}-\tfrac12\Big(\tfrac{5\pi}{12}-\tfrac{\pi}{12}\Big).\)
Values: \(\sin(4\cdot\tfrac{\pi}{12})=\sin(\tfrac{\pi}{3})=\tfrac{\sqrt3}{2}\),
\(\sin(4\cdot\tfrac{5\pi}{12})=\sin(\tfrac{5\pi}{3})=-\tfrac{\sqrt3}{2}\),
\(\sin(8\cdot\tfrac{\pi}{12})=\sin(\tfrac{2\pi}{3})=\tfrac{\sqrt3}{2}\),
\(\sin(8\cdot\tfrac{5\pi}{12})=\sin(\tfrac{4\pi}{3})=-\tfrac{\sqrt3}{2}\).
Hence \(A=\tfrac{5\pi}{6}+\tfrac{7\sqrt3}{8}\approx 4.134\).
✅ Answer: (B)
No-Calc Question
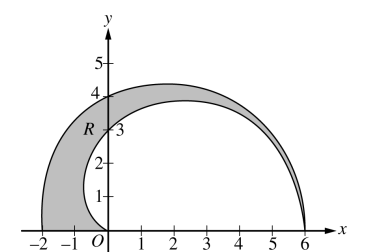
Let \(R\) be the region in the first and second quadrants between the polar curves \(f(\theta)=3+3\cos\theta\) and \(g(\theta)=4+2\cos\theta\), as shown. Which integral gives the area of \(R\)?
(B) \(\displaystyle \int_{0}^{\pi}\!\big(g(\theta)-f(\theta)\big)\,d\theta\)
(C) \(\displaystyle \tfrac12\int_{0}^{\pi}\!\big(g(\theta)-f(\theta)\big)^{2}\,d\theta\)
(D) \(\displaystyle \tfrac12\int_{0}^{\pi}\!\big(g(\theta)^{2}-f(\theta)^{2}\big)\,d\theta\)
▶️ Answer/Explanation
For area between polar curves \(r=R_{\text{outer}}(\theta)\) and \(r=R_{\text{inner}}(\theta)\) over \(\theta\in[\alpha,\beta]\):
\[ \text{Area}=\tfrac12\int_{\alpha}^{\beta}\Big(R_{\text{outer}}(\theta)^{2}-R_{\text{inner}}(\theta)^{2}\Big)\,d\theta. \] In the first and second quadrants, \(\theta\) runs from \(0\) to \(\pi\). From the figure and definitions, the outer radius is \(g(\theta)=4+2\cos\theta\) and the inner radius is \(f(\theta)=3+3\cos\theta\). Therefore, \[ \text{Area}=\tfrac12\int_{0}^{\pi}\Big(g(\theta)^{2}-f(\theta)^{2}\Big)\,d\theta. \] ✅ Answer: (D)
