AP Calculus BC 2.5 Applying the Power Rule - FRQs - Exam Style Questions
Calc-Ok Question
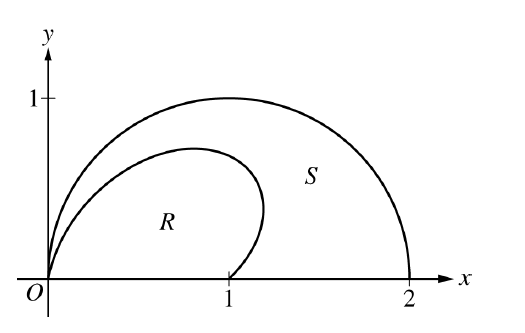
The figure shows the polar curves \(r=f(\theta)=1+\sin\theta\cos(2\theta)\) and \(r=g(\theta)=2\cos\theta\) for \(0\le\theta\le\frac{\pi}{2}\). Let \(R\) be the region in the first quadrant bounded by the curve \(r=f(\theta)\) and the \(x\)-axis. Let \(S\) be the region in the first quadrant bounded by the curve \(r=f(\theta)\), the curve \(r=g(\theta)\), and the \(x\)-axis.
(a) Find the area of \(R\).
(b) The ray \(\theta=k\), where \(0<k<\frac{\pi}{2}\), divides \(S\) into two regions of equal area. Write, but do not solve, an equation involving one or more integrals whose solution gives the value of \(k\).
(c) For each \(\theta\), \(0\le\theta\le\frac{\pi}{2}\), let \(w(\theta)\) be the distance between the points with polar coordinates \((f(\theta),\theta)\) and \((g(\theta),\theta)\). Write an expression for \(w(\theta)\). Find \(w_A\), the average value of \(w(\theta)\) over the interval \(0\le\theta\le\frac{\pi}{2}\).
(d) Using the information from part (c), find the value of \(\theta\) for which \(w(\theta)=w_A\). Is the function \(w(\theta)\) increasing or decreasing at that value of \(\theta\)? Give a reason for your answer.
Most-appropriate topic codes (CED):
• TOPIC 9.8 (BC): Area of a Polar Region — parts (a), (b)
• TOPIC 8.3: Using Accumulation Functions & Definite Integrals — average value & setup
• TOPIC 2.5–2.8: Product/Chain Rule & Trig Derivatives — sign of \(w'(\theta)\) in (d)
• TOPIC 8.3: Using Accumulation Functions & Definite Integrals — average value & setup
• TOPIC 2.5–2.8: Product/Chain Rule & Trig Derivatives — sign of \(w'(\theta)\) in (d)
▶️ Answer/Explanation
(a) Area of \(R\)
\(R\) is swept by \(r=f(\theta)\) from \(\theta=0\) to \(\theta=\frac{\pi}{2}\). \[ \text{Area}(R)=\frac12\int_{0}^{\pi/2}\!\big(f(\theta)\big)^{2}\,d\theta =\frac12\int_{0}^{\pi/2}\!\big(1+\sin\theta\cos2\theta\big)^{2}\,d\theta \approx \boxed{0.648414}\;(\approx \;0.648). \]
(b) Equal-area ray for \(S\)
The area between the curves is \(\displaystyle \frac12\int\big((g(\theta))^{2}-(f(\theta))^{2}\big)\,d\theta\). The ray \(\theta=k\) splits \(S\) into two equal parts iff \[ \boxed{\int_{0}^{k}\!\Big((g(\theta))^{2}-(f(\theta))^{2}\Big)\,d\theta \;=\;\int_{k}^{\pi/2}\!\Big((g(\theta))^{2}-(f(\theta))^{2}\Big)\,d\theta }. \] (Equivalently, \(\;\int_{0}^{k}(\cdots)\,d\theta=\tfrac12\int_{0}^{\pi/2}(\cdots)\,d\theta\).)
(c) Average radial gap
Distance along a fixed ray is the radial difference: \[ \boxed{w(\theta)=g(\theta)-f(\theta)=2\cos\theta-\big(1+\sin\theta\cos2\theta\big)}. \] Average value on \([0,\tfrac{\pi}{2}]\): \[ w_A=\frac{2}{\pi}\int_{0}^{\pi/2}\!w(\theta)\,d\theta =\frac{2}{\pi}\int_{0}^{\pi/2}\!\big(2\cos\theta-1-\sin\theta\cos2\theta\big)\,d\theta \approx \boxed{0.485446}\;(\approx \;0.485). \]
(d) Solve \(w(\theta)=w_A\) and monotonicity at that \(\theta\)
Numerically solve \(2\cos\theta-\big(1+\sin\theta\cos2\theta\big)=w_A\) on \((0,\tfrac{\pi}{2})\): \[ \boxed{\theta\;\approx\;0.517688\ \text{rad}\;(\approx 0.518)}. \] Differentiate \(w\): \[ w'(\theta)=g'(\theta)-f'(\theta) =(-2\sin\theta)-\big(\cos\theta\cos2\theta-2\sin\theta\sin2\theta\big). \] At \(\theta\approx 0.518\): \(\sin\theta\approx0.495,\ \cos\theta\approx0.868,\ \cos2\theta\approx0.510,\ \sin2\theta\approx0.859\). Then \[ f'(\theta)\approx 0.868(0.510)-2(0.495)(0.859)\approx -0.407,\quad g'(\theta)\approx -2(0.495)\approx -0.990, \] so \[ w'(\theta)\approx -0.990-(-0.407)=-0.583<0. \] Therefore \(w(\theta)\) is \(\boxed{\text{decreasing}}\) at \(\theta\approx0.518\).
\(R\) is swept by \(r=f(\theta)\) from \(\theta=0\) to \(\theta=\frac{\pi}{2}\). \[ \text{Area}(R)=\frac12\int_{0}^{\pi/2}\!\big(f(\theta)\big)^{2}\,d\theta =\frac12\int_{0}^{\pi/2}\!\big(1+\sin\theta\cos2\theta\big)^{2}\,d\theta \approx \boxed{0.648414}\;(\approx \;0.648). \]
(b) Equal-area ray for \(S\)
The area between the curves is \(\displaystyle \frac12\int\big((g(\theta))^{2}-(f(\theta))^{2}\big)\,d\theta\). The ray \(\theta=k\) splits \(S\) into two equal parts iff \[ \boxed{\int_{0}^{k}\!\Big((g(\theta))^{2}-(f(\theta))^{2}\Big)\,d\theta \;=\;\int_{k}^{\pi/2}\!\Big((g(\theta))^{2}-(f(\theta))^{2}\Big)\,d\theta }. \] (Equivalently, \(\;\int_{0}^{k}(\cdots)\,d\theta=\tfrac12\int_{0}^{\pi/2}(\cdots)\,d\theta\).)
(c) Average radial gap
Distance along a fixed ray is the radial difference: \[ \boxed{w(\theta)=g(\theta)-f(\theta)=2\cos\theta-\big(1+\sin\theta\cos2\theta\big)}. \] Average value on \([0,\tfrac{\pi}{2}]\): \[ w_A=\frac{2}{\pi}\int_{0}^{\pi/2}\!w(\theta)\,d\theta =\frac{2}{\pi}\int_{0}^{\pi/2}\!\big(2\cos\theta-1-\sin\theta\cos2\theta\big)\,d\theta \approx \boxed{0.485446}\;(\approx \;0.485). \]
(d) Solve \(w(\theta)=w_A\) and monotonicity at that \(\theta\)
Numerically solve \(2\cos\theta-\big(1+\sin\theta\cos2\theta\big)=w_A\) on \((0,\tfrac{\pi}{2})\): \[ \boxed{\theta\;\approx\;0.517688\ \text{rad}\;(\approx 0.518)}. \] Differentiate \(w\): \[ w'(\theta)=g'(\theta)-f'(\theta) =(-2\sin\theta)-\big(\cos\theta\cos2\theta-2\sin\theta\sin2\theta\big). \] At \(\theta\approx 0.518\): \(\sin\theta\approx0.495,\ \cos\theta\approx0.868,\ \cos2\theta\approx0.510,\ \sin2\theta\approx0.859\). Then \[ f'(\theta)\approx 0.868(0.510)-2(0.495)(0.859)\approx -0.407,\quad g'(\theta)\approx -2(0.495)\approx -0.990, \] so \[ w'(\theta)\approx -0.990-(-0.407)=-0.583<0. \] Therefore \(w(\theta)\) is \(\boxed{\text{decreasing}}\) at \(\theta\approx0.518\).
