A Gas (Review)
- Uniformly fills any container (have variable volume)
- Mixes spontaneously and completely with any other gas
- Exerts pressure on its surroundings
Pressure
- Is equal to force/unit area
- Pressure equals the number of collisions with the particles and its container
- Collision = force; container = area → more collisions = higher pressure
- Gasses have random motions and travel at high speeds → when they strike the side of the container they exert a force on that area = pressure
- SI units = newton/meter² = 1 Pascal (Pa)
The Gas Laws
Boyle’s Law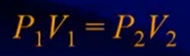
- Pressure and volume (and KE) are inversely related
- Temperature must be constant
- Units do not matter as long as they are the same on both sides
- A gas that strictly obeys Boyle’s law is called an ideal gas
Charles Law
- The volume of a gas is directly proportional to temperature
- Pressure must be constant
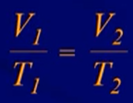
- Pressure must be constant
- In all gas laws, temperature must be in kelvin
- Gas is heated to a higher temperature → avg KE & speed of gas increase → they hit the walls more often/with more
- In order to keep the pressure constant, need to increase the volume of the container
Avogadro’s Law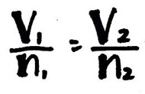
- The volume of a gas is directly proportional to the number of moles of gas
- Temperature and pressure must be constant
Gay-Lussac’s Law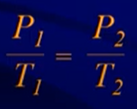
- Pressure and temperature are directly related
- Volume must be constant
Combined Gas Laws
- Not that common on AP exam
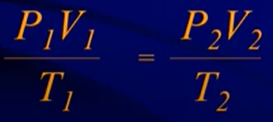
- If the moles of gas remains constant, use this formula and cancel out the other things that don’t change
The Ideal Gas Laws
- PV=nRT
- P = pressure in atm, torr, kPa
- V = volume in liters
- n = moles
- T = temperature in Kelvin
- R = ideal/universal gas constant (on reference sheet)
- = 0.08206 L atm K^-1 mol ^-1
- = 62.4 L torr K^-1 mol^-1
- = 8.314 L kPa K^-1 mol^-1
- A gas that obeys this equation is said to behave ideally
- Assumes that particles have no attraction
Gas Stoichiometry
- Standard Temperature and Pressure (STP): The conditions 0 ℃ and 1 atm
- The molar volume of an ideal gas is 22.42 L at STP
Gas Density and Molar Mass
Dalton’s Law of Partial Pressure
- Dalton’s law of partial pressures: the pressure exerted by a mixture of gases in a container is the sum of the individual pressure exerted by each gas if it were alone
- PTOTAL = P1 + P2 + P3 + …..
- P1 , P2 , P3 , represent each partial pressure: the pressure that a particular gas would exert if it were alone in the container.
- Partial Pressure Formula:
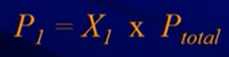
- Mole fraction() : Moles of gas / total gas moles (unitless)
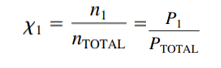
Valve Questions
- Have to use Boyle’s law to find P₂ and then add them up to calculate Ptotal
