Question
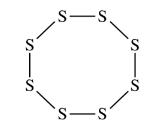
Elemental sulfur can exist as molecules with the formula \(S_8\) . The \(S_8\) molecule is represented by the incomplete Lewis diagram above.
(a) The diagram of \(S_8\) shows only bonding pairs of electrons. How many lone pairs of electrons does each S atom in the molecule have?
(b) Based on your answer to part (a), determine the expected value of the S–S–S bond angles in the S8 molecule.
(c) Write the electron configuration for the S atom in its ground state.
(d) The complete photoelectron spectrum for the element chlorine is represented below. Peak X in the spectrum corresponds to the binding energy of electrons in a certain orbital of chlorine atoms. The electrons in this orbital of chlorine have a binding energy of 273 MJ/mol, while the electrons in the same orbital of sulfur atoms have a binding energy of 239 MJ/mol.
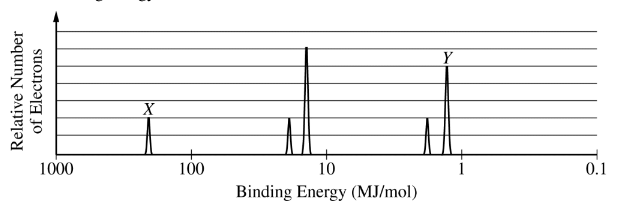
(i) Identify the orbital and explain the difference between the binding energies in terms of Coulombic forces.
(ii) Peak Y corresponds to the electrons in certain orbitals of chlorine atoms. On the spectrum shown, carefully draw the peak that would correspond to the electrons in the same orbitals of sulfur atoms.
\(3S_{8}+8OH^{-}\rightarrow 8S_{3}^{-}+4H00H\)
In an experiment, a student studies the kinetics of the reaction represented above and obtains the data shown in the following table.
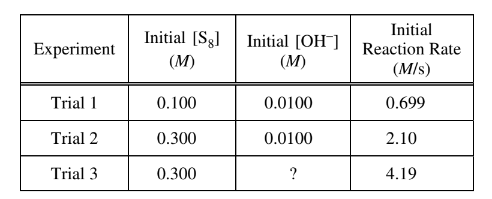
(e) Use the data in the table to do the following.
(i) Determine the order of the reaction with respect to \(S_8\) . Justify your answer.
(ii) Determine the value of\( [OH^−]\) that was used in trial 3, considering that the reaction is first order with respect to \(OH^−\). Justify your answer. The next day the student conducts trial 4 using the same concentrations of S 8 and \(OH^−\) as in trial 1, but the reaction occurs at a much slower rate than the reaction in trial 1. The student observes that the temperature in the lab is lower than it was the day before.
(f) Using particle-level reasoning, provide TWO explanations that help to account for the fact that the reaction rate is slower in trial 4.
▶️Answer/Explanation
(a) Two
(b)\(109.5^{\circ}\)
Acceptable range: \(104^{\circ}\leq angle \leq 110^{\circ}\).
(The experimentally determined angle is \(107^{\circ}8\)
(c) \(1s^{2} 2s^{2}2p^63s^2 3p^4\)
OR [Ne]\(3s^23p^4\)
(i) Peak X represents electrons in a 1s orbital. A Cl atom has one more proton in its nucleus than does a S atom; therefore, the electrons in Cl are more strongly attracted to the nucleus, and the binding energy of the 1s electrons in the Cl atom is greater than that of the 1s electrons in the S atom.
(ii) See example of a correct response (dashed peak) above.
(e)(i)

e(ii) Comparing trials 2 and 3, [S8] is kept constant and the initial reaction rate doubles. Since the reaction is first order with respect to\( OH^{-}\), the concentration of \(OH^{-}\) intrial 3 must be\( 2 \times 0.0100 M \)= 0.0200 M.
(f) The temperature was lower on the second day so the average kinetic energy of the reactant particles was lower. Therefore, there were fewer collisions between particles with sufficient
energy to react. Since the temperature was lower, the kinetic energy was lower and the average speed of the particles was lower. At the lower speeds, the reactant particles collided less frequently.
Question
To spectrophotometrically determine the mass percent of cobalt in an ore containing cobalt and some inert materials, solutions with known \([Co^{2+}]\) are prepared and the absorbance of each of the solutions is measured at the wavelength of optimum absorbance. The data are used to create a calibration plot, shown below.
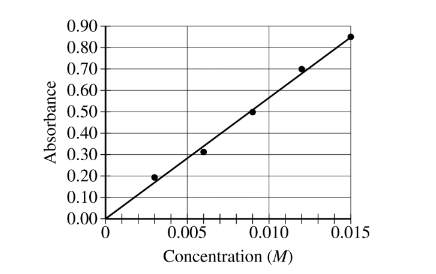
A 0.630 g sample of the ore is completely dissolved in concentrated \(HNO_3\)(aq). The mixture is diluted with water to a final volume of 50.00 mL. Assume that all the cobalt in the ore sample is converted to\( Co^{2+}\)(aq).
(a) What is the \([Co^{2+}]\) in the solution if the absorbance of a sample of the solution is 0.74 ?
(b) Calculate the number of moles of \(Co^{2+}\)(aq) in the 50.00 mL solution.
(c) Calculate the mass percent of Co in the 0.630 g sample of the ore.
▶️Answer/Explanation
(a) An absorbance of 0.74 corresponds to a concentration
of 0.0130 M (0.0125 M to 0.0135 M).
(b) \(0.05000L\times \frac{0.013molCo^{2+}}{1.00L}=6.50\times10^{-4}mol Co^{2+}\)
(c)
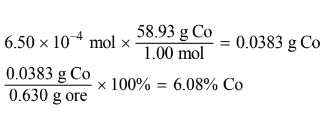
Question
Answer the following questions regarding light and its interactions with molecules, atoms, and ions.
(a) The longest wavelength of light with enough energy to break the Cl-Cl bond in \(Cl_2(g)\) is 495 nm.
(i) Calculate the frequency, in \(s^{-1}\), of the light.
(ii) Calculate the energy, in J, of a photon of the light.
(iii) Calculate the minimum energy, in kJ \(mol^{-1}\), of the Cl-Cl bond.
(b) A certain line in the spectrum of atomic hydrogen is associated with the electronic transition in the H from the sixth energy level (n = 6) to the second energy level (n = 2). atom
(i) Indicate whether the H atom emits energy or whether it absorbs energy during the transition. Justify your answer.
(ii) Calculate the wavelength, in nm, of the radiation associated with the spectral line.
(iii) Account for the observation that the amount of energy associated with the same electronic transition (n = 6 to rz = 2) in the \(He^+\) ion is greater than that associated with the corresponding transition in the H atom.
▶️Answer/Explanation
Answer:
(a) (i) \(v=\frac{c}{\lambda}=\frac{3.00 \times 10^{17}nm/sec}{495nm}(or,=\frac{3.00 \times 10^8m/sec}{495 \times 10^{-9}m})=6.06 \times 10^{14} sec^{-1}\)
(ii) \(E=hv=(6.626 \times 10^{-34}J sec)(6.06 \times 10^{14} sec^{-1}) = 4.02 \times 10^{-19}J\)
(iii) \((4.02 \times 10^{-19}J)(6.022 \times 10^{-23}mol^{-1})(0.00100kJ/J)=242 kJ/mol\)
(b) (i) Energy is emitted.
The n = 6 state is at a higher energy than the n=2 state. Going from a high energy state to low energy state means that energy must be emitted.
(ii) \(E_2=\frac{-2.178 \times 10^{-18} J}{2^2}=-5.45 \times 10^{-19}J, E_6 = \frac{-2.178 \times 10^{-18}J}{6^2}=-6.05 \times 10^{-20}J\)
\(\Delta E = E_6 – E_2 = -6.05 \times 10^{-20}J- (-5.45 \times 10^{-19}J) = 4.84 \times 10^{-19}J)= 4.84 \times 10^{-19}J\)
OR,
\(\Delta E = 2.178 \times 10^{-18}(\frac{1}{2^2}-\frac{1}{6^2})J = 2.178 \times 10^{-18}(0.2222)J = 4.84 \times 10^{-19}J\)
\(E=\frac{hc}{\lambda} \Rightarrow \lambda = \frac{hc}{E}\)
OR,
\(v=\frac{E}{h}=\frac{4.84 \times 10^{-19}J}{6.626 \times 10^{-34}J sec}=7.30 \times 10^{14} sec^{-1}\)
\(\lambda = \frac{(6.626 \times 10^{-34}J sec)(3.00 \times 10^{17} nm sec^{-1}}{4.84 \times 10^{-19}J}=411 nm\)
OR,
\(\lambda = \frac{(6.626 \times 10^{-34}J sec)(3.00 \times 10^{17}nm sec^{-1})}{4.84 \times 10^{-19}J}=411 nm\)
(iii) The positive charge holding the electron is greater for \(He^+\), which has a 2+ nucleus, than for H with its 1+ nucleus. The stringer attraction means that it requires more energy for the electron to move to higher energy levels. Therefore, transitions form high energy state to lower states will be more energetic for \(He^+\) than for H.
