Question
A student is doing experiments with CO2(g). Originally, a sample of the gas is in a rigid container at 299 K and 0.70 atm. The student increases the temperature of the CO2(g) in the container to 425 K.
(a) Describe the effect of raising the temperature on the motion of the CO2(g) molecules.
(b) Calculate the pressure of the CO2(g) in the container at 425 K.
(c) In terms of kinetic molecular theory, briefly explain why the pressure of the CO2(g) in the container changes as it is heated to 425 K.
(d) The student measures the actual pressure of the CO2(g) in the container at 425 K and observes that it is less than the pressure predicted by the ideal gas law. Explain this observation.
▶️Answer/Explanation
Ans:
(a)
| The average speed of the molecules increases as temperature increases. |
(b)
Both volume and the number of molecules are constant, therefore \(\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\Rightarrow \frac{0.70 atm}{299 K}=\frac{P_{2}}{425 K}\Rightarrow P_{2}=0.99 atm\) |
(c)
| Faster-moving gas particles collide more frequently with the walls of the container, thus increasing the pressure. OR Faster-moving gas particles collide more forcefully with the walls of the container, thus increasing the pressure. |
(d)
| The attractive forces between CO2 molecules result in a pressure that is lower than that predicted by the ideal gas law. |
Question
What two properties of real gases cause deviation from ideal behavior?
▶️Answer/Explanation
Ans:
In contrast to the assumptions used for ideal gases, real molecules and atoms have finite (not zero) volumes, and they
do attract one another.
Question
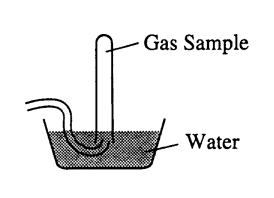
A student collected a sample of hydrogen gas by the displacement of water as shown by the diagram above. The relevant data are given in the following table.

(a) Calculate the number of moles of hydrogen gas collected.
(b) Calculate the number of molecules of water vapor in the sample of gas.
(c) Calculate the ratio of the average speed of the hydrogen molecules to the average speed of the water vapor molecules in the sample.
(d) Which of the two gases, H2 or H2O, deviates more from ideal behavior? Explain your answer.
▶️Answer/Explanation
Ans:
(a) \(n = \frac{PV}{RT}=\frac{(721)(0.090)}{(62.4)(298)}=3.49 \times 10^{-3}molH_{2}\)
25°C → 298 K
745 – 24 = 721 mm Hg
calculation of moles of H2
(b) \(\frac{(23.8)(0.090)}{(62.4)(298)}=1.15 \times 10^{-4}molH_{2}O\)
(1.15 x 10B4)(6.03 x 1023) – 6.92 x 1019 molecules H2O
(c) The average kinetic energies are equal, so
\(\left ( \frac{1}{2}mv^{2} \right )H_{2}O=\left ( \frac{1}{2}mv^{2} \right )H_{2}.\)
\(\frac{v_{H_{2}}}{v_{H_{2}}o}=\sqrt{\frac{MM_{H_{2}}O}{MM_{H_{2}}}}=\sqrt{\frac{18}{2}}=3\)
Note: credit also given for correct use of \(v_{rms}=\sqrt{\frac{3RT}{M}}.\)
(d) H2O deviates more from ideal behavior.
Explanation:
EITHER
i) The volume of the H2O molecule is larger than that of the H2 molecule
OR,
ii) The intermolecular forces among H2O molecules are stronger than those among H2 molecules
