Question
Nitrogen dioxide, \(NO_2\)(g), is produced as a by-product of the combustion of fossil fuels in internal combustion engines. At elevated temperatures NO2(g) decomposes according to the equation below.
\(2 NO_2(g) → 2 NO(g) + O_2\)(g)
The concentration of a sample of \(NO_2\(g) is monitored as it decomposes and is recorded on the graph directly below. The two graphs that follow it are derived from the original data
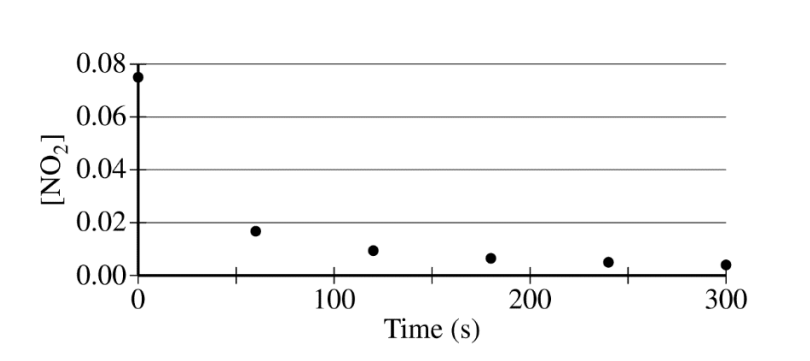
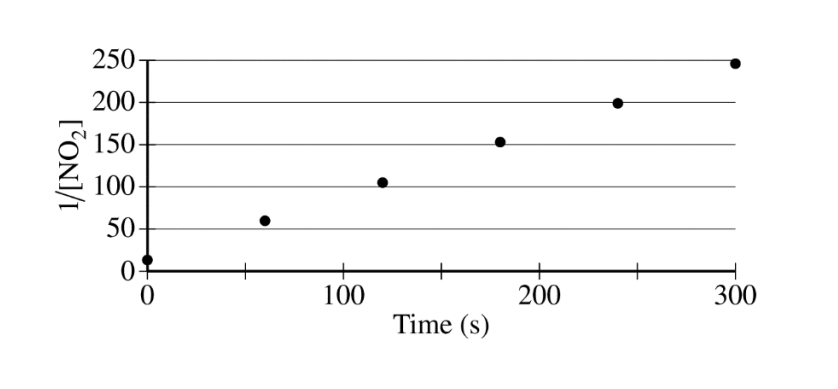
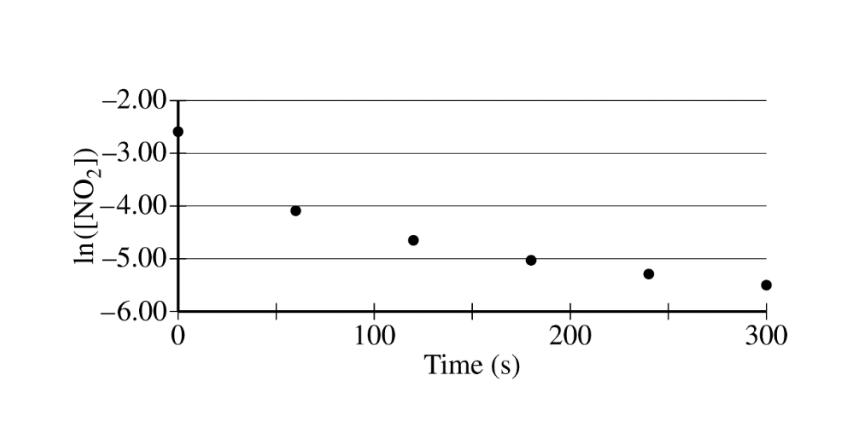
(a) Explain how the graphs indicate that the reaction is second order.
(b) Write the rate law for the decomposition of \(NO_2\)(g).
(c) Consider two possible mechanisms for the decomposition reaction.
(i) Is the rate law described by mechanism I shown below consistent with the rate law you wrote in part (b) ? Justify your answer.
Mechanism I
Step 1: NO2(g) + NO2(g) → NO(g) + NO3(g) slow
Step 2: NO3(g) → NO(g) + O2(g) fast
(ii) Is the rate law described by mechanism II shown below consistent with the rate law you wrote in part (b) ? Justify your answer.
Mechanism II
Step 1: NO2(g) + NO2(g) ⇔ N2O4(g) fast equilibrium
Step 2: N2O4(g) → 2 NO(g) + O2(g) slow
▶️Answer/Explanation
Ans:
(a)
| The linear graph of \(\frac{1}{[NO_{2}]}\) vs. time indicates a second-order reaction. |
(b)
| rate = k[NO2]2 |
(c) (i)
| Yes, Step 1 is slow, therefore it is the rate-determining step of this mechanism. The rate law of this elementary reaction is rate = k[NO2][NO2] = k[NO2]2, which is consistent with the second – order rate law in part (b). |
(ii)
| Yes, Step 2 is slow; therefore, it is the rate – determining step of this mechanism. The rate law of this elementary reaction is rate = k[N2O2]. Because N2O4 is an intermediate, it cannot appear in the rate law of the overall reaction. Because \(K_{eq}\frac{[N_{2}O_{4}]}{[NO_{2}]^{2}}\) in step 1, [N2O4] = Keq[NO2]2. Then, substituting Keq[NO2]2 for [N2O4] in the rate law of step 2 gives rate = (k Keq) [NO2]2 , which is consistent with the rate law in part (b). |
Question
2 C4H6(g) → C8H12(g)
At high temperatures the compound C4H6 (1,3-butadiene) reacts according to the equation above. The rate of the reaction was studied at 625 K in a rigid reaction vessel. Two different trials, each with a different starting concentration, were carried out. The data were plotted in three different ways, as shown below.
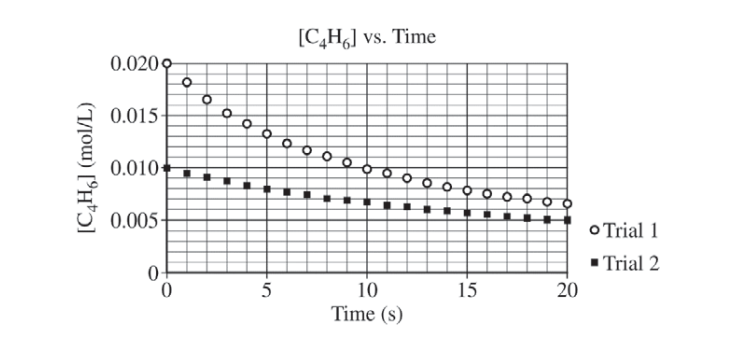
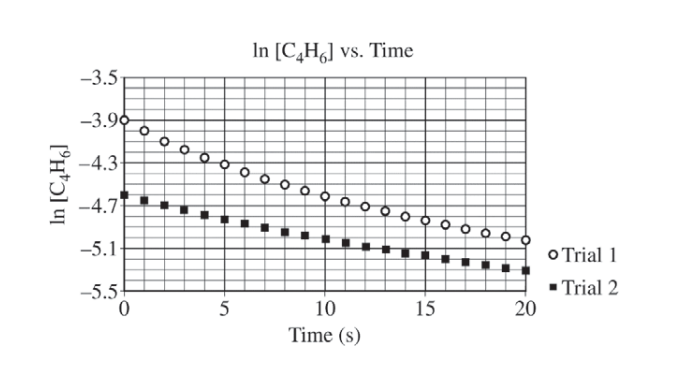
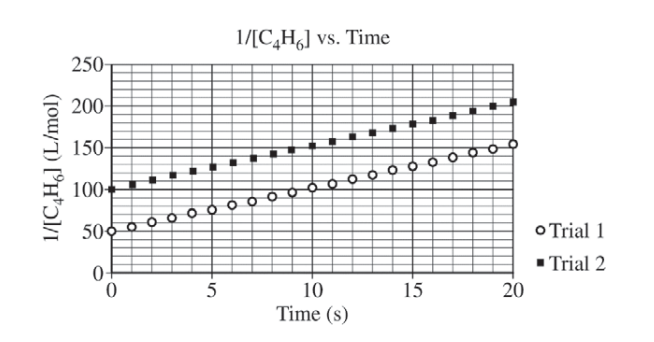
(a) For trial 1, calculate the initial pressure, in atm, in the vessel at 625 K. Assume that initially all the gas present in the vessel is C4H6 .
(b) Use the data plotted in the graphs to determine the order of the reaction with respect to C4H6 .
(c) The initial rate of the reaction in trial 1 is 0.0010 mol/(L⋅s). Calculate the rate constant, k, for the reaction at 625 K.
▶️Answer/Explanation
Ans:
(a)
For trial 1, \(\frac{n}{V}= 0.020 mol/L\) (or assume the volume of the vessel is 1.0 L; the number of moles of C4H6 \(P =\frac{nRT}{V}= \frac{(0.020 mol)(0.08206 L atm mol^{-1}K^{-1})(625 K)}{1.0 L}=1.0 atm\) |
(b)
| Second order (because the plot of 1/[C4H6] is a straight line). |
(c)
| From the second-order rate law (differential form): rate = k[C4H6]2 \(\Rightarrow k = \frac{rate}{([C_{4}H_{6}])^{2}}=\frac{0.0010 mol/(L\cdot s)}{(0.020 mol/L)^{2}}=2.5 L/(mol\cdot s)\) OR From the second-order rate law (integrated form): \(\frac{1}{[C_{4}H_{6}]_{t}}= 2kt + \frac{1}{[C_{4}H_{6}]_{0}}\) The coefficient of t is equal to 2k because of the reaction stoichiometry. The slope of the line in the plot of \(\frac{1}{[C_{4}H_{6}]}\) versus time is 2k. Thus slope = 5.0 L/(mol·s) = 2k , therefore k = 2.5 L/(mol·s). Note: Students who choose the second method of determining k but omit the factor of 2, thereby getting an answer of 5.0 L/(mol·s), still earn the point |
