Question
\(CaO(s)+H_{2}O(l)\rightarrow Ca(OH)_{2}(s) \Delta H^{\circ}_{rxn}=-63.7kj/mol_{rxn}\)
Calcium oxide, CaO(s), has been proposed as a substance that can be used to heat water quickly for portable heating packs or for cooking. When placed in water, CaO(s) reacts as shown by the equation above.
(a) A student wants to design a heating pad that could heat a 150.0 g sample of water from \(25.0^{\circ}C to 60.0^{\circ}C. 4.18J/(g.^{\circ}C).) \)
(i) Calculate the amount of heat, in joules, that the water must absorb for its temperature to change by this amount. (Assume that the specific heat capacity of the water is \(4.18 J/(g.^{\circ}C)\)
(ii) Calculate the minimum mass of CaO(s) that the student would need to use in order to cause this temperature change.
(b) The student hypothesizes that the design of the heating pad could be changed to enable it to heat 150.0 g of water from \(25.0^{\circ}C to 90.0^{\circ}C\) by using a greater mass of CaO(s).
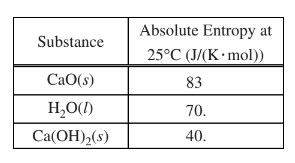
(i) Use the data in the table below to determine the standard entropy change, \(\Delta S^{\circ}_{rxn}, in J/(K.mol_{rxn}) \Delta S^{\circ}_{rxn} and \Delta H^{\circ}_{rxn} \)for the reaction.
(ii) Is the reaction thermodynamically favorable at 90.0°C? Justify your answer with a calculation. (Assume that both \(\Delta S^{\circ}_{rxn}\) and \( \Delta H^{\circ}_{rxn}\) are constant between 25.0°C and 90.0°C.) The student learns that the \(Ca(OH)_2\) produced from the reaction is relatively insoluble and that it dissolves in water according to the equation below.
\(Ca(OH)_{2}(s)\rightarrow Ca^{2+}(aq)+2OH^{-}(aq)\)
(c) The student prepares a saturated solution of Ca(OH)2 and determines that the \([Ca^{2+}] \)is 0.011 M. Calculate
the value of\( K_{sp}\) for \(Ca(OH)_{2}\)
The student wishes to significantly increase the molar solubility of the. \(Ca(OH)_{2}(s)\) and has access to the following substances.
15 mL of distilled water 15 mL of 1.0 M KOH(aq)
15 mL of 1.0 M\( CaCl_2\)(aq) 15 mL of 1.0 M HCl(aq)
(d) Which substance, when added to the \(Ca(OH)_2\) mixture, would increase the molar solubility most significantly? Justify your choice based on concepts of chemical equilibrium, such as Le Châtelier’s principle.
▶️Answer/Explanation
a(i)\(q=mc\Delta T = 150.0 g x 4.18 J/(g °C) x (60.0°C -25.0°C) = 2.19 x 104 J\)
a(ii)
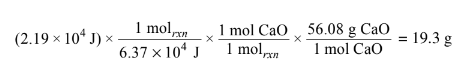
b(i) \(\Delta S°_rxn \) = ∑S° products – ∑S° reactants
= \(40. J/(K.mol) – [83 J/(K.mol) + 70. J/(K.mol)]\)
= \(-113 J/(K.mol_{rxn})\)
b(ii) Yes, because \(\Delta G° is negative. \Delta G° = \Delta H° – T \Delta S° =-63.7 kJ/mol_{rxn} K (-113 J/(K.mol_{rxn})) ×\frac{1kj}{1000j} = -22.7 kJ/mol_{rxn}\)
(c) \( [OH^-] = 2 × [Ca^2+] = 2 (0.011 M) = 0.022 \)\(M K_sp=[Ca^2+] [OH^-]^2 = (0.011)(0.022)^2 = 5.3 × 10^-6\)
(d) HCl
The \(H^+\) from the HCl reacts with \(OH^−\), decreasing \([OH^−]\). The loss of\( OH^−\) results in non-equilibrium conditions in the\( Ca(OH)_2\) dissolution. More\( Ca(OH)_2\) must dissolve to increase\( [OH^{−}]\), increasing the molar solubility as Q approaches K and the system returns to equilibrium.
Question
A student is asked to determine what mass of butane, \(C_4H_10\)(g), needs to burn in order to raise the temperature of a 1650 g beaker of sand by 180.°C. The student is provided with the equipment shown below.
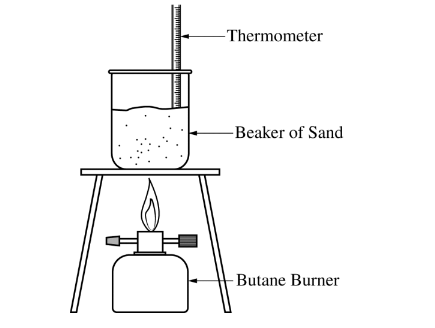
(a) Calculate the amount of heat energy needed to raise the temperature of the beaker of sand by 180.°C. Assume that all the heat energy from the burner is transf erred to the beaker of sand and that the specific heat capacity of the beaker and sand together is 0.810 J/(g⋅°C). The student runs the experiment and collects the data shown in the table below.

(b) Calculate the number of moles of butane that was used in the experiment. Report your answer to the appropriate number of significant figures. The combustion of butane is represented by the equation below.
\(C_{4}H_{10}(g)+\frac{13}{2}O_{2}(g)\rightarrow 5H_{2}O(g)+4CO_{2}(g) \) \(\Delta ^{\circ}_{rxn}=-2659kj/mol_{rxn}\)
(c) Using the balanced equation for the combustion of butane and \Delta ^{\circ}_{rxn} , determine the amount of heat energy produced by the combustion of butane in the experiment.
(d) The student claims that some of the heat energy produced by the combustion of butane was lost to the air surrounding the system. Do your answers to parts (a) and (c) support the student’s claim? Explain
▶️Answer/Explanation
.
(a)\( q= mc\Delta T\)
\(q=(1650g)\left ( 0.810\frac{j}{g.^{\circ}C} \right ) = 241,000 J = 241 kJ\)
(b) 225.26 g – 218.20 g = 7.06 g butane
\(7.06g\times \frac{1mol}{58.12g butane} = 0.121 mol butane\)
(c)\(0.121 mol butane \times \frac{2659kjproduced}{1mol butane}=322kj\)
(d) Yes, the answers to parts (a) and (c) support the hypothesis. The amount of heat generated from the combustion of the butane ism greater than the amount of heat required to cause the temperature change of the sand, indicating that some of the heat from the combustion of butane was lost.
Question
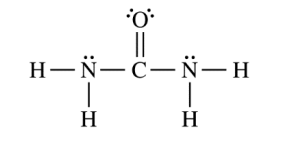
The compound urea, H2NCONH2 , is widely used in chemical fertilizers. The complete Lewis electron-dot diagram for the urea molecule is shown above.
(a) Identify the hybridization of the valence orbitals of the carbon atom in the urea molecule.
(b) Urea has a high solubility in water, due in part to its ability to form hydrogen bonds. A urea molecule and four water molecules are represented in the box below. Draw ONE dashed line (—-) to indicate a possible location of a hydrogen bond between a water molecule and the urea molecule.

The dissolution of urea is represented by the equation above. A student determines that 5.39 grams of H2NCONH2 (molar mass 60.06 g/mol) can dissolve in water to make 5.00 mL of a saturated solution at 20.°C.
(c) Calculate the concentration of urea, in mol/L, in the saturated solution at 20.°C.
(d) The student also determines that the concentration of urea in a saturated solution at 25°C is 19.8 M. Based on this information, is the dissolution of urea endothermic or exothermic? Justify your answer in terms of Le Chatelier’s principle.
(e) The equipment shown above is provided so that the student can determine the value of the molar heat of solution for urea. Knowing that the specific heat of the solution is 4.18 J/(g⋅°C), list the specific measurements that are required to be made during the experiment.
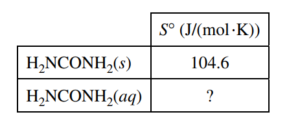
(f) The entropy change for the dissolution of urea, ΔS0soln , is 70.1 J/(mol⋅K) at 25°C. Using the information in the table above, calculate the absolute molar entropy, S°, of aqueous urea.
(g) Using particle-level reasoning, explain why ΔS0soln is positive for the dissolution of urea in water.
(h) The student claims that ΔS° for the process contributes to the thermodynamic favorability of the dissolution of urea at 25°C. Use the thermodynamic information above to support the student’s claim.
▶️Answer/Explanation
Ans:
(a)
| sp2 |
(b)
| A dashed line should connect a hydrogen atom in water to a nitrogen or oxygen atom in urea or an oxygen atom in water to a hydrogen atom in urea. One possible correct response is shown above. |
(c)
5.39 g H2NCONH2 × \(\frac{1 mol}{60.06 g}=0.0897 mol\) \(\frac{0.0897 mol}{0.00500 L}=17.9 M\) |
(d)
| The increased solubility at the higher temperature implies that the dissolution of urea is endothermic. If a saturated solution of urea is heated, then the equilibrium system is stressed. The stress is counteracted by the endothermic dissolution of more urea. |
(e)
| mass of urea, mass of water, initial temperature of water, final temperature of solution |
(f)
ΔS0soln = S0 (H2NCONH2(aq)) – S0 (H2NCONH2(s)) 70.1 J/(mol.K) = S0 (H2NCONH2(aq)) – 104.6 J/(mol.K) S0 (H2NCONH2(aq)) = 174.7 J/(mol.K) |
(g)
| Urea molecules in solution have a greater number of possible arrangements than in solid urea. This increased number of arrangements corresponds to a positive ΔS0soln. |
(h)
| Thermodynamic favorability for a process at standard conditions is determined by the sign of ΔG0 , with ΔG0 =ΔH0 -TΔS0 . Since ΔS0 is positive, the TΔS0 term makes the value of ΔG0 smaller and thus makes the dissolution more thermodynamically favorable. |
