Question
A student is asked to determine what mass of butane, \(C_4H_10\)(g), needs to burn in order to raise the temperature of a 1650 g beaker of sand by 180.°C. The student is provided with the equipment shown below.
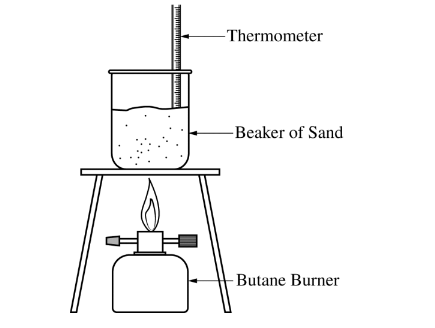
(a) Calculate the amount of heat energy needed to raise the temperature of the beaker of sand by 180.°C. Assume that all the heat energy from the burner is transf erred to the beaker of sand and that the specific heat capacity of the beaker and sand together is 0.810 J/(g⋅°C). The student runs the experiment and collects the data shown in the table below.

(b) Calculate the number of moles of butane that was used in the experiment. Report your answer to the appropriate number of significant figures. The combustion of butane is represented by the equation below.
\(C_{4}H_{10}(g)+\frac{13}{2}O_{2}(g)\rightarrow 5H_{2}O(g)+4CO_{2}(g) \) \(\Delta ^{\circ}_{rxn}=-2659kj/mol_{rxn}\)
(c) Using the balanced equation for the combustion of butane and \(\Delta ^{\circ}_{rxn} \), determine the amount of heat energy produced by the combustion of butane in the experiment.
(d) The student claims that some of the heat energy produced by the combustion of butane was lost to the air surrounding the system. Do your answers to parts (a) and (c) support the student’s claim? Explain
▶️Answer/Explanation
.
(a)\( q= mc\Delta T\)
\(q=(1650g)\left ( 0.810\frac{j}{g.^{\circ}C} \right ) = 241,000 J = 241 kJ\)
(b) 225.26 g – 218.20 g = 7.06 g butane
\(7.06g\times \frac{1mol}{58.12g butane} = 0.121 mol butane\)
(c)\(0.121 mol butane \times \frac{2659kjproduced}{1mol butane}=322kj\)
(d) Yes, the answers to parts (a) and (c) support the hypothesis. The amount of heat generated from the combustion of the butane ism greater than the amount of heat required to cause the temperature change of the sand, indicating that some of the heat from the combustion of butane was lost.
