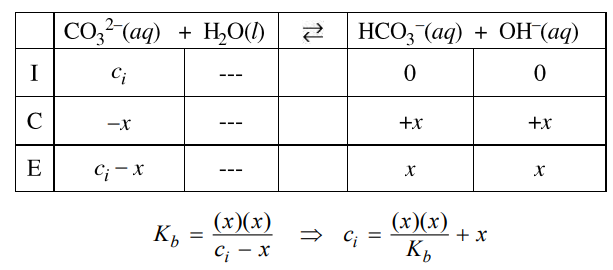Question.
\(2NaHCO_{3}(s)\rightarrow Na_{2}CO_{3}+CO_{2}(g)+H_{2}O(g)\)
\( NaHCO_3\)(s) (baking soda) decomposes upon heating to produce \(Na_2CO_3(s) \)and two gaseous products, as shown by the equation above.
(a) A student claims that the reaction is an oxidation-reduction reaction because the oxidation number of carbon changes. Do you agree with the claim? In your answer include the oxidation number of carbon in each of the three carbon-containing species in the reaction. The student conducts an experiment to determine the composition of a mixture of \(NaHCO_3\) (molar mass 84.01 g/mol) and \(Na_2CO_3\) (molar mass 105.99 g/mol). The student places a sample of the mixture into a preweighed test tube that is attached to a container that holds a drying agent. The student heats the test tube strongly with a Bunsen burner for 10 minutes, during which time all of the water produced by the reaction is captured by the drying agent. The following table shows the data the student recorded during the experiment.

(b) Calculate the number of moles of\( NaHCO_3(s)\) present in the mixture in the test tube before the reaction was initiated.
(c) Determine the mass percent of\( NaHCO_3(s)\) in the mixture.
(d) If the student spills some of the mixture out of the test tube after weighing the test tube and mixture and before heating, how would this error affect the mass percent of \(NaHCO_3\) calculated in part (c) ? Justify your answer. When a sample of pure\( Na_2CO_3 \)is placed in distilled water, the student observes that the pH of the solution increases significantly. This process is represented by the balanced net-ionic equation shown below.
\(CO_{3}^{2-}(aq)+H_2O{l}\rightleftharpoons HCO_{3}^-+OH^{-}(aq)\)
(e) The student prepares a 0.10 M \(Na_2CO_3(aq)\) solution and measures the pH of the solution to be 11.65.
(i) Calculate\( [OH^{-}]\) in the \(Na_2CO_3\)(aq) solution.
(ii) Write the expression for \(K_b\) for the carbonate ion.
(iii) Calculate the value of \(K_b \)for the carbonate ion. The student adds some 1.0 M Sr\((NO_3)_2\)(aq) to the 0.10 M\( Na_2CO_3(aq)\) and observes the formation of a precipitate.
(f) Write the balanced net-ionic equation for the reaction between Sr\((NO_3)_2\) and \(Na_2CO_3\) that produces the precipitate.
▶️Answer/Explanation
(a) No. The oxidation number of carbon is +4 in each of the three carbon-containing species.
(b)
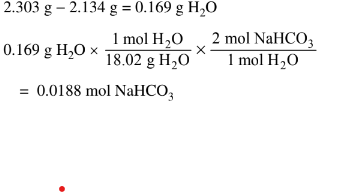
(c) \(0.0188mol NaHCO_{3}\times \frac{84.01g NaHCO_{3}}{1molNaHCO_{3}}\frac{1.58g}{(17.648g-15.825g)}\times =86.7%\)
(d) The calculated mass percent would be smaller than the actual value. Less water would be collected, so there would appear to be less\( NaHCO_3\) in the sample.
(e)(i) \(pOH = 14.00 – 11.65 = 2.35\)
\([OH^−] = 10-2.35 = 4.5\times 10^-{3}\)
e(ii) \(k_b=\frac{[HCO_{3}^{-}][OH^-]}{CO_{3}^{2-}}\)
e(iii) \(K_b=\frac{(4.5\times 10^{-3})\times (4.5\times 10^{-3})}{0.10-(4.5\times 10^{-3})}\approx \frac{(4.5\times 10^{-3})^2}{0.10}= 2.0\times 10^{-4}\)
(f) \(Sr^{2+}CO_{3}^{2-}\rightarrow SrCO_{3}\)
Question
A student is given 50.0 mL of a solution of Na2CO3 of unknown concentration. To determine the concentration of the solution, the student mixes the solution with excess 1.0 M Ca(NO3)2(aq), causing a precipitate to form.
The balanced equation for the reaction is shown below.
Na2CO3(aq) + Ca(NO3)2(aq) → 2 NaNO3(aq) + CaCO3(s)
(a) Write the net ionic equation for the reaction that occurs when the solutions of Na2CO3 and Ca(NO3)2 are mixed.
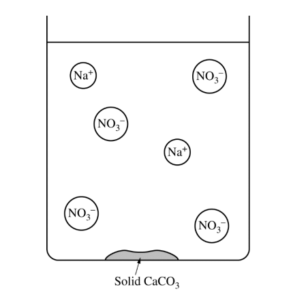
(b) The diagram below is incomplete. Draw in the species needed to accurately represent the major ionic species remaining in the solution after the reaction has been completed.
The student filters and dries the precipitate of CaCO3 (molar mass 100.1 g/mol) and records the data in the table below.

(c) Determine the number of moles of Na2CO3 in the original 50.0 mL of solution.
(d) The student realizes that the precipitate was not completely dried and claims that as a result, the calculated Na2CO3 molarity is too low. Do you agree with the student’s claim? Justify your answer.
(e) After the precipitate forms and is filtered, the liquid that passed through the filter is tested to see if it can conduct electricity. What would be observed? Justify your answer.
The student decides to determine the molarity of the same Na2CO3 solution using a second method. When
Na2CO3 is dissolved in water, CO32−(aq) hydrolyzes to form HCO3−(aq), as shown by the following equation.
CO32−(aq) + H2O(l) ⇔ HCO3−(aq) + OH−(aq) \(K_{b}=\frac{[HC{O_{3}}^{-}][OH^{-}]}{[{CO_{3}}^{2-}]}=2.1\times 10^{-4}\)
(f) The student decides to first determine [OH−] in the solution, then use that result to calculate the initial concentration of CO32−(aq).
(i) Identify a laboratory method (not titration) that the student could use to collect data to determine [OH−] in the solution.
(ii) Explain how the student could use the measured value in part (f)(i) to calculate the initial concentration of CO32−(aq). (Do not do any numerical calculations.)
(g) In the original Na2CO3 solution at equilibrium, is the concentration of HCO3−(aq) greater than, less than, or equal to the concentration of CO32−(aq) ? Justify your answer.
(h) The student needs to make a CO32−/HCO3− buffer. Is the Na2CO3 solution suitable for making a buffer with a pH of 6? Explain why or why not.
▶️Answer/Explanation
Ans:
(a)
| Ca2+(aq) + CO32-(aq) → CaCO3(s) |
(b)
| The drawing shows one Ca2+ ion. |
(c)
\(0.93 g CaCO_{3}\times \frac{1 mol CaCO_{3}}{100.1 g}=0.0093 mol CaCO_{3}\) \(0.0093 mol CaCO_{3}\times \frac{1 mol Na_{2}CO_{3}}{1 molCaCO_{3} }=0.0093 mol Na_{2}CO_{3}\) |
(d)
| Disagree. The presence of water in the solid will cause the measured mass of the precipitate to be greater than the actual mass of CaCO3. As a result, the calculated number of moles of CaCO3 and moles of Na2CO3 will be greater than the actual moles present. Therefore the calculated concentration of Na2CO3(aq) will be too high. |
(e)
| The liquid conducts electricity because ions (Na+(aq), Ca2+(aq), and NO3–(aq) are present in the solution. |
(f) (i)
| Determine the pH of the solution using a pH meter. |
(ii)
First determine [OH–] using pOH = 14 – pH, then [OH–] = 10-pOH. Then, use the Kb expression and an ICE table (see example below to determine [CO32-] and [HCO3–] at equilibrium. The initial concentration of CO32-, ci, is equal to the sum of the equilibrium concentrations of CO32- and HCO3–.
|
(g)
| Less than. The small value of Kb, 2.1 × 10-4, indicates that the reactants are favored. |
(h)
| No, the Na2CO3 solution is not suitable. The pKa of HCO3– is 10.32. Buffers are effective when the required pH is approximately equal to the pKa of the weak acid. An acid with a pKa of 10.32 is not appropriate to prepare a buffer with a pH of 6. |
Question
HF(aq) + H2O(l) ⇔ F−(aq) + H3O+(aq)
The ionization of HF(aq) in water is represented by the equation above. In a 0.0350 M HF(aq) solution, the percent ionization of HF is 13.0 percent.
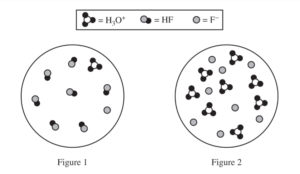
(a) Two particulate representations of the ionization of HF molecules in the 0.0350 M HF(aq) solution are shown below in Figure 1 and Figure 2. Water molecules are not shown. Explain why the representation of the ionization of HF molecules in water in Figure 1 is more accurate than the representation in Figure 2. (The key below identifies the particles in the representations.)
(b) Use the percent ionization data above to calculate the value of Ka for HF.
(c) If 50.0 mL of distilled water is added to 50.0 mL of 0.035 M HF(aq), will the percent ionization of HF(aq) in the solution increase, decrease, or remain the same? Justify your answer with an explanation or calculation.
▶️Answer/Explanation
Ans:
(a)
| HF is a weak acid and is only partially ionized. This fact is consistent with Figure 1, which shows that one out of eight (∼13%) HF molecules is ionized (to form one H3O+ and one F–). OR Figure 2 cannot represent HF because it represents 100% ionization of the acid. |
(b)
Assum [H3O+] = [F–] in HF(aq). \(\frac{[H_{3}O^{+}]}{0.050 M}=0.130\Rightarrow [H_{3}O^{+}]=0.00455 M\) HF(aq) + H2O(l) ⇔ F–(aq) + H3O+(aq) I 0.0350 0 ∼0 \(K_{a}=\frac{[H_{3}O^{+}][F^{-}]}{[HF]}=\frac{(0.00455)^{2}}{(0.0304)}=6.81\times 10^{-4}\) |
(c)
The percent ionization of HF in the solution would increase. Doubling the volume of the solution decreases the initial concentration of each species by one-half; therefore, \(Q=\frac{(\frac{1}{2}[H_{3}O^{+}]_{i})(\frac{1}{2}[F^{-}]_{i})}{\frac{1}{2}[HF]_{i}}=\frac{1}{2}K_{a}\Rightarrow Q<K_{a}.\) Consequently the equilibrium position will shift toward the products and increase the percent ionization. OR New volume = twice original volume, thus new \([HF]_{i}=\frac{0.035}{2}=0.0175 M\) \(K_{a}=\frac{[H_{3}O^{+}][F^{-}]}{[HF]}=6.81\times 10^{-4}\) (value from part (b)) Let [H3O+] = [F– ] = x Then \(6.81\times 10^{-4}=\frac{(x)(x)}{(0.0175-x)}\approx \frac{x^{2}}{(0.0175)}\Rightarrow x\approx 0.00345 M\) Percent ionization \(\frac{0.00345 M}{0.0175 M}\times 100=20.%\) 20.% > 13.0%; therefore, the percent ionization increases. |