Question
HF(aq) + H2O(l) ⇔ F−(aq) + H3O+(aq)
The ionization of HF(aq) in water is represented by the equation above. In a 0.0350 M HF(aq) solution, the percent ionization of HF is 13.0 percent.
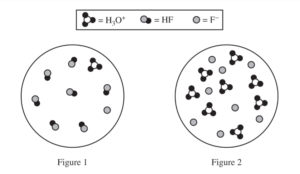
(a) Two particulate representations of the ionization of HF molecules in the 0.0350 M HF(aq) solution are shown below in Figure 1 and Figure 2. Water molecules are not shown. Explain why the representation of the ionization of HF molecules in water in Figure 1 is more accurate than the representation in Figure 2. (The key below identifies the particles in the representations.)
(b) Use the percent ionization data above to calculate the value of Ka for HF.
(c) If 50.0 mL of distilled water is added to 50.0 mL of 0.035 M HF(aq), will the percent ionization of HF(aq) in the solution increase, decrease, or remain the same? Justify your answer with an explanation or calculation.
▶️Answer/Explanation
Ans:
(a)
| HF is a weak acid and is only partially ionized. This fact is consistent with Figure 1, which shows that one out of eight (∼13%) HF molecules is ionized (to form one H3O+ and one F–). OR Figure 2 cannot represent HF because it represents 100% ionization of the acid. |
(b)
Assum [H3O+] = [F–] in HF(aq). \(\frac{[H_{3}O^{+}]}{0.050 M}=0.130\Rightarrow [H_{3}O^{+}]=0.00455 M\) HF(aq) + H2O(l) ⇔ F–(aq) + H3O+(aq) I 0.0350 0 ∼0 \(K_{a}=\frac{[H_{3}O^{+}][F^{-}]}{[HF]}=\frac{(0.00455)^{2}}{(0.0304)}=6.81\times 10^{-4}\) |
(c)
The percent ionization of HF in the solution would increase. Doubling the volume of the solution decreases the initial concentration of each species by one-half; therefore, \(Q=\frac{(\frac{1}{2}[H_{3}O^{+}]_{i})(\frac{1}{2}[F^{-}]_{i})}{\frac{1}{2}[HF]_{i}}=\frac{1}{2}K_{a}\Rightarrow Q<K_{a}.\) Consequently the equilibrium position will shift toward the products and increase the percent ionization. OR New volume = twice original volume, thus new \([HF]_{i}=\frac{0.035}{2}=0.0175 M\) \(K_{a}=\frac{[H_{3}O^{+}][F^{-}]}{[HF]}=6.81\times 10^{-4}\) (value from part (b)) Let [H3O+] = [F– ] = x Then \(6.81\times 10^{-4}=\frac{(x)(x)}{(0.0175-x)}\approx \frac{x^{2}}{(0.0175)}\Rightarrow x\approx 0.00345 M\) Percent ionization \(\frac{0.00345 M}{0.0175 M}\times 100=20.%\) 20.% > 13.0%; therefore, the percent ionization increases. |
