Question
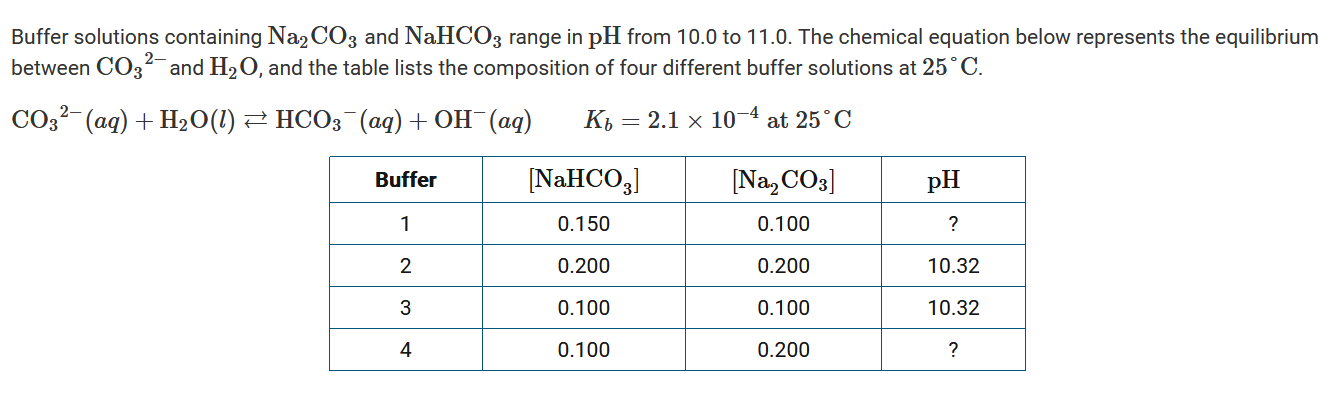
Which of the following mathematical expressions can be used to determine the approximate pH of buffer 1 ?
A \(pH=[-log(2.1\times 10^{−4})]+log(\frac{0.100}{0.150})=3.50\)
B \(pH=[-log(2.1\times 10^{−4})]+log(\frac{0.150}{0.100})=3.85\)
C \(pH=[14.00+log(2.1\times 10^{−4})]+log(\frac{0.150}{0.150})=10.50\)
D \(pH=[14.00+log(2.1\times 10^{−4})]+log(\frac{0.150}{0.100})=10.50\)
▶️Answer/Explanation
Ans:C
Since the solutions are at 25°C, \(K_b\times K_a=K_w\), hence \(pK_b+pK_a=pK_w=14.00\) Using \(pH=pK_a+log(\frac{[A^−]}{[HA]}\) and substituting \([14.00+log(2.1\times 10^{−4})]\) for \(pK_a\), \(pH=[14.00+log(2.1\times 10^{−4})]+log(\frac{0.150}{0.100})=10.15\). This pH is reasonable, since the buffer has a higher concentration of the conjugate acid \(HCO_3^−\) compared with the weak base \(CO_3^{2−}\); thus, the pH should be slightly lower than 10.32 (compared with buffers 2 and 3).
Question

Which mathematical expression can be used to explain why buffer 2 and buffer 3 have the same pH?
A \(log(\frac{0.200}{0.200})=log(\frac{0.100}{0.100})=log(1)\)
B \(−log(K_w)−[−log(K_b)]=pK_a\)
C \(0.200M=2\times (0.100M)\)
D \(0.200M−0.200M=0.100M−0.100M\)
▶️Answer/Explanation
Ans:A
Both buffers are made with the same components; thus, what determines the pH is the ratio of weak base to conjugate acid. The ratio is the same for both buffers; therefore, \(log(\frac{0.200}{0.200})=log(\frac{0.100}{0.100})=log(1)=0\) and the \(pH=pK_a\) of the conjugate acid \(HCO_3^−\).
Question

Which mathematical expression can be used to explain why buffer 2 and buffer 3 have the same pH?
A \(log(\frac{0.200}{0.200})=log(\frac{0.100}{0.100})=log(1)\)
B \(−log(K_w)−[−log(K_b)]=pK_a\)
C \(0.200M=2\times (0.100M)\)
D \(0.200M−0.200M=0.100M−0.100M\)
▶️Answer/Explanation
Ans:A
Both buffers are made with the same components; thus, what determines the pH is the ratio of weak base to conjugate acid. The ratio is the same for both buffers; therefore, \(log(\frac{0.200}{0.200})=log(\frac{0.100}{0.100})=log(1)=0\) and the \(pH=pK_a\) of the conjugate acid \(HCO_3^−\).
Question
\(CH_3COOH(aq)+H_2O(l)\)⇄\(H_3O^+(aq)+CH_3COO^−(aq)\) \(pK_a=4.76\) at 25°C
The equilibrium representing the acid dissociation of CH3COOH is shown above. A buffer solution is prepared by adding 0.10mol of \(NaOH(s)\) to 1.00L of 0.30M \(CH_3COOH\). Assuming the change in volume is negligible, which of the following expressions will give the pH of the resulting buffer at 25°C?
A \(pH=4.76+log\frac{0.10}{0.30}\)
B \(pH=4.76+log\frac{0.10}{0.20}\)
C \(pH=4.76+log\frac{0.20}{0.10}\)
D \(pH=4.76+log\frac{0.30}{0.10}\)
▶️Answer/Explanation
Ans:B
After the addition of 0.10 mol of \(NaOH(s)\) to 1.00L of 0.30M \(CH_3COOH\), 0.10mol of \(NaCH_3COO\) is produced. This leaves 0.20mol of \(CH_3COOH\)remaining. Because the volume is 1.00L, the resulting molar concentration of \(CH_3COOH\) is 0.20M and \([NaCH_3COO]=0.10M\). Since \(pH=pK_a+log\frac{[A^−]}{[HA]}\) , \(pH=4.76+log\frac{0.10}{0.20}\).
Question
The Henderson-Hasselbalch equation is __________.
A) pH = \(pK_a + log \frac{[base]}{[acid]}\)
B) pH = log \(\frac{[acid]}{[acid]}\)
C) pH = \(pK_a – log \frac{[base]}{[acid]}\)
D) \([H^]=k_a + \frac{[base]}{[acid]}\)
E) pH = \(pK_a + log \frac{[acid]}{[base]}\)
▶️Answer/Explanation
Ans: A
