Ideal Gas Behavior
- For real gases, the deviation from ideal behavior and predicted pressure is due to the InterMF that occur between real gases & the fact that the particle of real gases have volume → PV does not equal nRT
- The gas which gas deviates the most from ideal behavior will be the one with the strongest IMF forces bcuz the pressure predicted will not be as accurate (particles will strike less) → actual pressure is smaller than predicted
- The best conditions to make a gas most ideal is high temperature and low pressure (HoT LiPs)
- Gases exhibit non-ideal behavior at..
- Low temp & high pressures
- When particles have significant intermolecular forces and molecular size
Effect of Particle Volume
- Particle volume becomes significant → actual pressure is greater than predicted
- Low pressures = the space between molecules is much greater than the volume of molecules themselves → gas behaves more ideally
- High pressure = particle volume greatly reduces the volume in which the particles are free to move → gas behavior is non-ideal
The Meaning of Temperature
- Kelvin temperature indicates the average kinetic energy of the gas particles & index of random motions of the particles of a gas → higher temperature = greater motion
- KE per mol =
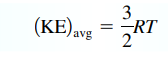; KE per molecule = 
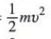(on RFS)
Root Mean Square Velocity
(final units are in m/s)
Effusion and Diffusion
- Diffusion: describes the mixing of gases
- The rate of diffusion is the rate of the mixing of gases.
- Effusion: describes the movement of a gas through a small hole
Effusion
- Graham’s law of effusion.
:(M = molar masses)
Diffusion
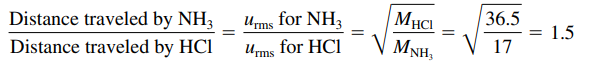l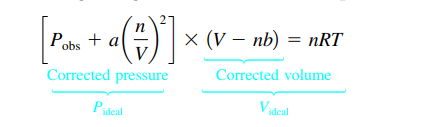
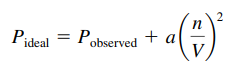
- The value of a reflects how much of a correction must be made to adjust the observed pressure up to the expected ideal pressure