Rate Laws: An Introduction
- Initial Rate Method: the “instantaneous rate” just after the reaction beings; Usually the fastest
 →
→ 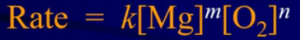
- K = rate constant; m and n = rate orders
- Rate Constant (k): relates the rate of the reaction to the concentration of the reactants = slope
- Value of k is positive for slope of products and negative for the slope of reaction
- Value of this constant is dependent on temperature and units reflect the overall reaction order
- TRICK: units for k are always going to be molarity to the negative one number less than the reaction order / unit of time
2 Important Concepts (when writing a rate law)
- The concentrations of the products are not in the rate law
- The value of m/n can only be determined experimentally-not from the coefficients of the overall equation
- Except for elementary reactions
Types of Rate Laws
- Differential Rate Law/the Rate Law: expresses how rate depends on concentration
- Integrated rate law: expresses how the concentrations depend on time
- Use integrated rate law when asked to find how much of a reactant/product at certain time
Finding Rate Law Given Data Table
- Find two experiments where the concentration of one reactant is changing and the other reactant remains the same
- Rate Formula 1 / Rate Formula 2 → solve for rate orders → plug in values in rate formula and solve for K
Overall Reaction Order
- Find the overall reaction order → add up each rate order
- Ex:
 → Overall reaction order is 1 +2 + 3 = 6
→ Overall reaction order is 1 +2 + 3 = 6
- Ex:
- Greater the order/exponent = the faster the reactant is being consumed
Determining the Form of the Rate Law (aA → products)
- The reaction starts as a first-order reaction because the rate depends on the number of reactant molecules adsorbed by the catalyst. However, once all the surface sites of the catalyst are fully occupied, the rate is no longer affected by the concentration of the reactant and the reaction becomes zero-order
