AP Chemistry 6.8 Enthalpies of Formation Study Notes - New Syllabus Effective fall 2024
AP Chemistry 6.8 Enthalpies of Formation Study Notes.- New syllabus
AP Chemistry 6.8 Enthalpies of Formation Study Notes – AP Chemistry – per latest AP Chemistry Syllabus.
LEARNING OBJECTIVE
Calculate the enthalpy change for a chemical or physical process based on the standard enthalpies of formation.
Key Concepts:
- Calculating Enthalpy Change Using Standard Enthalpies of Formation
Calculating Enthalpy Change Using Standard Enthalpies of Formation
The standard enthalpy change of a reaction (\( \mathrm{\Delta H^\circ_{reaction}} \)) represents the total energy change when a reaction occurs under standard conditions (1 atm, 298 K, and 1 M concentration for aqueous solutions). It can be determined using standard enthalpies of formation of reactants and products.
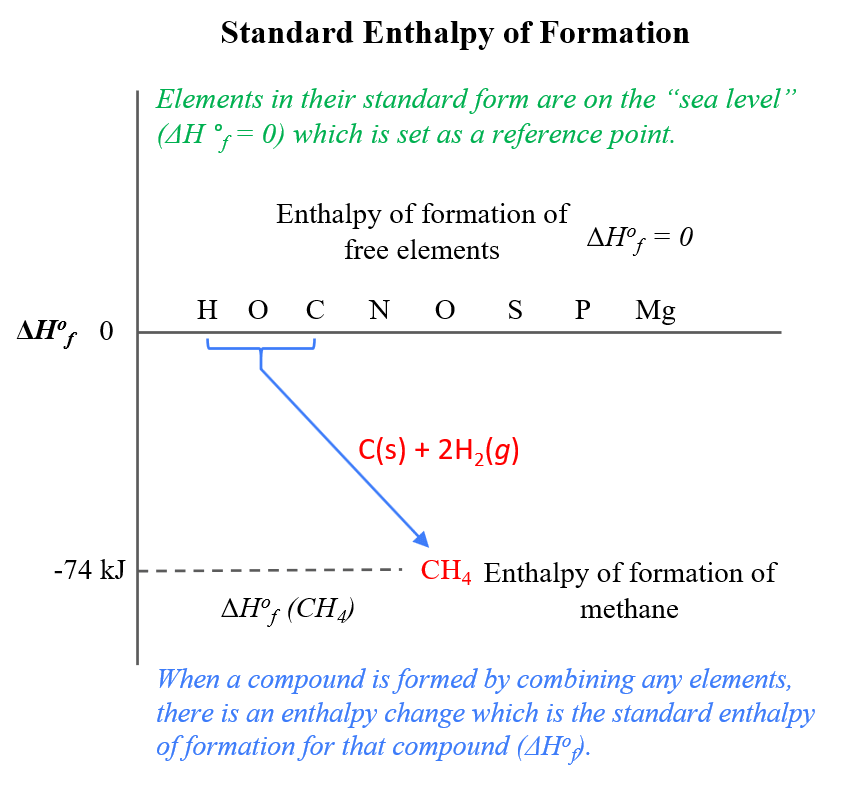
- The standard enthalpy of formation (\( \mathrm{\Delta H_f^\circ} \)) is the enthalpy change when 1 mole of a compound is formed from its elements in their standard states.
- For elements in their standard states (e.g., \( \mathrm{O_2(g)} \), \( \mathrm{N_2(g)} \), \( \mathrm{H_2(g)} \), \( \mathrm{C_{(graphite)}} \)), \( \mathrm{\Delta H_f^\circ = 0} \).
Formula
\( \mathrm{\Delta H^\circ_{reaction} = \sum \Delta H_f^\circ (products) – \sum \Delta H_f^\circ (reactants)} \)
- \( \mathrm{\Delta H_f^\circ (products)} \): Sum of standard enthalpies of formation for all products, multiplied by their stoichiometric coefficients.
- \( \mathrm{\Delta H_f^\circ (reactants)} \): Sum of standard enthalpies of formation for all reactants, multiplied by their coefficients.
- Units are typically \( \mathrm{kJ/mol} \).
Key Relationships
- \( \mathrm{\Delta H^\circ < 0} \): Exothermic reaction → energy released → surroundings warm up.
- \( \mathrm{\Delta H^\circ > 0} \): Endothermic reaction → energy absorbed → surroundings cool down.
- This relationship links macroscopic heat flow to molecular formation energies.
Key Idea: Standard enthalpies of formation allow calculation of reaction enthalpy by comparing the total bond energy of products and reactants. If the reaction releases energy (\( \mathrm{\Delta H^\circ < 0} \)) → exothermic; if it absorbs energy (\( \mathrm{\Delta H^\circ > 0} \)) → endothermic.
Example :
Use standard enthalpies of formation to calculate \( \mathrm{\Delta H^\circ_{reaction}} \) for the combustion of propane:
Reaction: \( \mathrm{C_3H_8(g) + 5O_2(g) \rightarrow 3CO_2(g) + 4H_2O(l)} \)
Given Data:
\( \mathrm{\Delta H_f^\circ(C_3H_8) = -103.8\ kJ/mol} \)
\( \mathrm{\Delta H_f^\circ(CO_2) = -393.5\ kJ/mol} \)
\( \mathrm{\Delta H_f^\circ(H_2O(l)) = -285.8\ kJ/mol} \)
\( \mathrm{\Delta H_f^\circ(O_2) = 0\ kJ/mol} \)
▶️ Answer / Explanation
Step 1: Write the formula:
\( \mathrm{\Delta H^\circ_{rxn} = \sum \Delta H_f^\circ(products) – \sum \Delta H_f^\circ(reactants)} \)
Step 2: Substitute the values:
\( \mathrm{\Delta H^\circ_{rxn} = [3(-393.5) + 4(-285.8)] – [(-103.8) + 5(0)]} \)
Step 3: Calculate:
\( \mathrm{\Delta H^\circ_{rxn} = (-1180.5 – 1143.2) – (-103.8)} \)
\( \mathrm{\Delta H^\circ_{rxn} = -2223.7 + 103.8 = -2119.9\ kJ/mol} \)
Step 4: Interpretation:
- \( \mathrm{\Delta H^\circ = -2119.9\ kJ/mol} \)
- Negative → energy is released → exothermic reaction.
Final Answer: \( \mathrm{\Delta H^\circ_{rxn} = -2119.9\ kJ/mol} \); combustion of 1 mol of propane releases 2119.9 kJ of heat.
Example :
Calculate \( \mathrm{\Delta H^\circ_{reaction}} \) for the decomposition of calcium carbonate using standard enthalpies of formation:
Reaction: \( \mathrm{CaCO_3(s) \rightarrow CaO(s) + CO_2(g)} \)
Given Data:
\( \mathrm{\Delta H_f^\circ(CaCO_3) = -1206.9\ kJ/mol} \)
\( \mathrm{\Delta H_f^\circ(CaO) = -635.1\ kJ/mol} \)
\( \mathrm{\Delta H_f^\circ(CO_2) = -393.5\ kJ/mol} \)
▶️ Answer / Explanation
Step 1: Apply the formula:
\( \mathrm{\Delta H^\circ_{rxn} = \sum \Delta H_f^\circ(products) – \sum \Delta H_f^\circ(reactants)} \)
Step 2: Substitute values:
\( \mathrm{\Delta H^\circ_{rxn} = [(-635.1) + (-393.5)] – [(-1206.9)]} \)
Step 3: Simplify:
\( \mathrm{\Delta H^\circ_{rxn} = (-1028.6) – (-1206.9)} \)
\( \mathrm{\Delta H^\circ_{rxn} = +178.3\ kJ/mol} \)
Step 4: Interpretation:
- \( \mathrm{\Delta H^\circ = +178.3\ kJ/mol} \)
- Positive → heat is absorbed → endothermic reaction.
Final Answer: \( \mathrm{\Delta H^\circ_{rxn} = +178.3\ kJ/mol} \); decomposition of 1 mol of calcium carbonate absorbs 178.3 kJ of heat.
