AP Chemistry 9.9 Cell Potential and Free Energy Study Notes - New Syllabus Effective fall 2024
AP Chemistry 9.9 Cell Potential and Free Energy Study Notes- New syllabus
AP Chemistry 9.9 Cell Potential and Free Energy Study Notes – AP Chemistry – per latest AP Chemistry Syllabus.
LEARNING OBJECTIVE
Explain whether an electrochemical cell is thermodynamically favored, based on its standard cell potential and the constituents half – reaction within the cell.
Key Concepts:
- Fundamentals of Electrochemistry and Cell Potential
- Calculating Standard Cell Potentials from Half-Reactions
- Relationship Between \( \mathrm{\Delta G^\circ} \), \( \mathrm{E^\circ_{cell}} \), and Reaction Spontaneity
Fundamentals of Electrochemistry and Cell Potential
Electrochemistry is the study of redox (oxidation–reduction) reactions that involve the transfer of electrons and their relationship to electrical energy. These reactions occur in electrochemical cells, which can either generate electricity from spontaneous reactions or require electrical energy to drive nonspontaneous ones.
Each electrochemical cell produces or consumes an electric potential (voltage) depending on the thermodynamic favorability of the reaction.
Key Relationships Between Thermodynamics and Cell Potential
- If the redox reaction is spontaneous → \( \mathrm{\Delta G^\circ < 0} \), \( \mathrm{E^\circ_{cell} > 0} \)
- If the redox reaction is nonspontaneous → \( \mathrm{\Delta G^\circ > 0} \), \( \mathrm{E^\circ_{cell} < 0} \)
Thus, the sign of the cell potential (\( \mathrm{E^\circ_{cell}} \)) indicates whether the reaction can occur spontaneously.
Types of Electrochemical Cells
| Cell Type | Thermodynamic Nature | Sign of \( \mathrm{E^\circ_{cell}} \) | Energy Conversion |
|---|---|---|---|
| Galvanic (Voltaic) | Spontaneous reaction | \( \mathrm{E^\circ_{cell} > 0} \) | Chemical → Electrical |
| Electrolytic | Nonspontaneous reaction | \( \mathrm{E^\circ_{cell} < 0} \) | Electrical → Chemical |
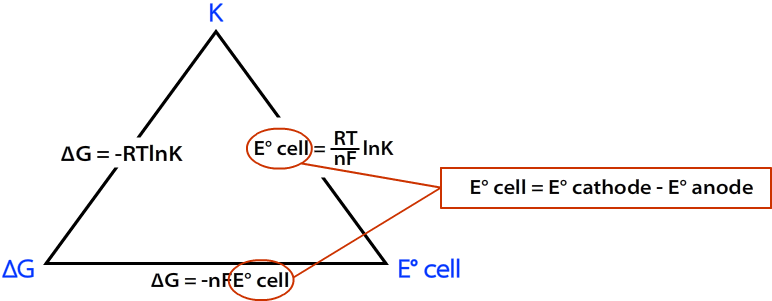
Key Formula — Connection Between Energy and Potential
\( \mathrm{\Delta G^\circ = -nFE^\circ_{cell}} \)
- \( \mathrm{\Delta G^\circ} \): Standard Gibbs free energy change (J/mol)
- \( \mathrm{n} \): Moles of electrons transferred in the redox reaction
- \( \mathrm{F = 96,485\ C/mol\ e^-} \): Faraday’s constant
- \( \mathrm{E^\circ_{cell}} \): Standard cell potential (V)
Interpretation of Voltage (Cell Potential)
- \( \mathrm{E^\circ_{cell}} \) represents the driving force for electron flow in a redox reaction.
- Positive \( \mathrm{E^\circ_{cell}} \) → electrons flow spontaneously from anode to cathode.
- Negative \( \mathrm{E^\circ_{cell}} \) → requires external energy source to proceed.
Example:
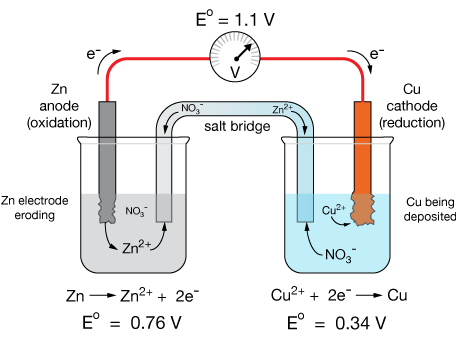
The standard cell potential for the reaction \( \mathrm{Zn(s) + Cu^{2+}(aq) \rightarrow Zn^{2+}(aq) + Cu(s)} \) is \( \mathrm{E^\circ_{cell} = +1.10\ V} \). Determine whether the reaction is spontaneous and what type of cell it represents.
▶️ Answer / Explanation
Step 1: Given \( \mathrm{E^\circ_{cell} = +1.10\ V} \).
Step 2: Use \( \mathrm{\Delta G^\circ = -nFE^\circ_{cell}} \):
\( \mathrm{\Delta G^\circ = -(2)(96,485)(1.10) = -212,000\ J/mol = -212\ kJ/mol} \)
Step 3: Interpretation:
- \( \mathrm{\Delta G^\circ < 0} \): spontaneous reaction.
- \( \mathrm{E^\circ_{cell} > 0} \): galvanic cell.
Final Answer: The reaction is spontaneous under standard conditions and represents a galvanic cell converting chemical energy into electrical energy.
Calculating Standard Cell Potentials from Half-Reactions
The standard cell potential (\( \mathrm{E^\circ_{cell}} \)) of an electrochemical cell can be determined by identifying the oxidation and reduction half-reactions and using their respective standard reduction potentials (\( \mathrm{E^\circ_{red}} \)).
These potentials are measured under standard conditions: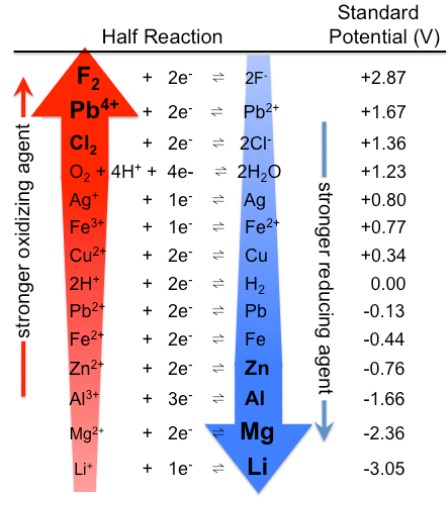
- Temperature: 298 K
- Pressure: 1 atm (for gases)
- Concentration: 1 M (for aqueous ions)
Key Formula for Calculating Cell Potential
\( \mathrm{E^\circ_{cell} = E^\circ_{cathode} – E^\circ_{anode}} \)
- \( \mathrm{E^\circ_{cathode}} \): reduction potential where reduction occurs
- \( \mathrm{E^\circ_{anode}} \): reduction potential of the species oxidized (converted to oxidation potential by sign reversal)
Important Note: The standard reduction potential table always lists reduction half-reactions. If a half-reaction is reversed (oxidation), the sign of its potential must also be reversed.
Procedure for Calculating \( \mathrm{E^\circ_{cell}} \)
- Write the two half-reactions (one reduction, one oxidation).
- Identify which occurs at the anode (oxidation) and which at the cathode (reduction).
- Use the equation \( \mathrm{E^\circ_{cell} = E^\circ_{cathode} – E^\circ_{anode}} \).
- Do not multiply potentials by coefficients — potentials are intensive properties.
Conceptual Summary
- \( \mathrm{E^\circ_{cell} > 0} \): spontaneous (galvanic cell)
- \( \mathrm{E^\circ_{cell} < 0} \): nonspontaneous (electrolytic cell)
- \( \mathrm{E^\circ_{cell} = 0} \): equilibrium under standard conditions
Example:
Determine the standard cell potential for the reaction:
\( \mathrm{Zn(s) + Cu^{2+}(aq) \rightarrow Zn^{2+}(aq) + Cu(s)} \)
Given data:
- \( \mathrm{E^\circ_{red}(Cu^{2+}/Cu) = +0.34\ V} \)
- \( \mathrm{E^\circ_{red}(Zn^{2+}/Zn) = -0.76\ V} \)
▶️ Answer / Explanation
Step 1: Identify half-reactions.
- Anode (oxidation): \( \mathrm{Zn(s) \rightarrow Zn^{2+}(aq) + 2e^-} \)
- Cathode (reduction): \( \mathrm{Cu^{2+}(aq) + 2e^- \rightarrow Cu(s)} \)
Step 2: Apply the formula.
\( \mathrm{E^\circ_{cell} = E^\circ_{cathode} – E^\circ_{anode}} \)
\( \mathrm{E^\circ_{cell} = (+0.34) – (-0.76) = +1.10\ V} \)
Step 3: Interpretation.
- \( \mathrm{E^\circ_{cell} = +1.10\ V} \) → spontaneous reaction.
- Electrons flow from Zn (anode) to Cu (cathode).
Final Answer: The standard cell potential is \( \mathrm{+1.10\ V} \). The Zn–Cu cell is galvanic and operates spontaneously.
Example:
Using the data below, determine which reaction will occur spontaneously when the following half-cells are connected:
- \( \mathrm{Ag^+ + e^- \rightarrow Ag(s)} \), \( \mathrm{E^\circ = +0.80\ V} \)
- \( \mathrm{Cu^{2+} + 2e^- \rightarrow Cu(s)} \), \( \mathrm{E^\circ = +0.34\ V} \)
▶️ Answer / Explanation
Step 1: The more positive \( \mathrm{E^\circ_{red}} \) occurs at the cathode (reduction site).
- Cathode: \( \mathrm{Ag^+ + e^- \rightarrow Ag(s)} \)
- Anode: \( \mathrm{Cu(s) \rightarrow Cu^{2+} + 2e^-} \)
Step 2: Calculate the cell potential.
\( \mathrm{E^\circ_{cell} = E^\circ_{cathode} – E^\circ_{anode}} \)
\( \mathrm{E^\circ_{cell} = +0.80 – (+0.34) = +0.46\ V} \)
Step 3: Interpretation:
- \( \mathrm{E^\circ_{cell} > 0} \) → spontaneous reaction.
- Electrons flow from Cu (anode) → Ag (cathode).
Final Answer: The spontaneous reaction is \( \mathrm{Cu(s) + 2Ag^+ \rightarrow Cu^{2+} + 2Ag(s)} \), with \( \mathrm{E^\circ_{cell} = +0.46\ V} \).
Relationship Between \( \mathrm{\Delta G^\circ} \), \( \mathrm{E^\circ_{cell}} \), and Reaction Spontaneity
The standard Gibbs free energy change (\( \mathrm{\Delta G^\circ} \)) and the standard cell potential (\( \mathrm{E^\circ_{cell}} \)) are directly related measures of a reaction’s thermodynamic favorability.
A positive cell potential corresponds to a negative free energy change — meaning the redox reaction is spontaneous under standard conditions.
Key Formula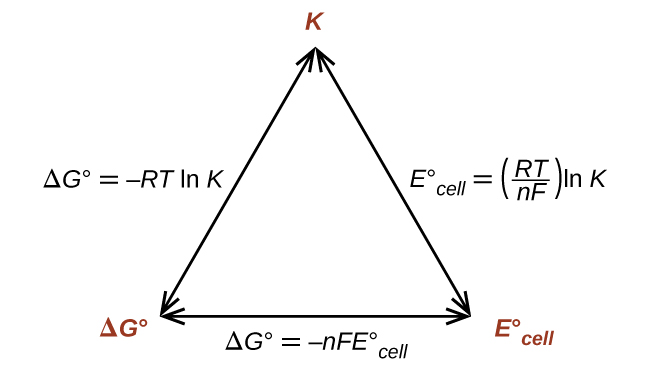
\( \mathrm{\Delta G^\circ = -nFE^\circ_{cell}} \)
- \( \mathrm{\Delta G^\circ} \): Standard Gibbs free energy change (J/mol)
- \( \mathrm{n} \): Moles of electrons transferred in the balanced redox reaction
- \( \mathrm{F = 96,485\ C/mol\ e^-} \): Faraday’s constant
- \( \mathrm{E^\circ_{cell}} \): Standard cell potential (V)
This relationship connects electrical work (voltage × charge) to chemical energy change (Gibbs energy).
Thermodynamic Interpretation
| \( \mathrm{E^\circ_{cell}} \) | \( \mathrm{\Delta G^\circ} \) | Thermodynamic Meaning | Reaction Type |
|---|---|---|---|
| \( \mathrm{> 0} \) | \( \mathrm{< 0} \) | Spontaneous | Galvanic (Voltaic) |
| \( \mathrm{< 0} \) | \( \mathrm{> 0} \) | Nonspontaneous | Electrolytic |
| \( \mathrm{= 0} \) | \( \mathrm{= 0} \) | Equilibrium | No net redox reaction |
Connecting to the Equilibrium Constant
At standard conditions, Gibbs free energy also relates to the equilibrium constant \( \mathrm{K} \):
\( \mathrm{\Delta G^\circ = -RT \ln K} \)
Combining with \( \mathrm{\Delta G^\circ = -nFE^\circ_{cell}} \):
\( \mathrm{E^\circ_{cell} = \dfrac{RT}{nF} \ln K} \)
Thus, \( \mathrm{E^\circ_{cell}} \) is directly proportional to \( \ln K \): a larger equilibrium constant corresponds to a higher cell voltage and a more spontaneous process.
Key Idea: The relationship \( \mathrm{\Delta G^\circ = -nFE^\circ_{cell}} \) connects chemical and electrical energy:
- \( \mathrm{E^\circ_{cell} > 0} \) → \( \mathrm{\Delta G^\circ < 0} \): spontaneous, galvanic cell.
- \( \mathrm{E^\circ_{cell} < 0} \) → \( \mathrm{\Delta G^\circ > 0} \): nonspontaneous, electrolytic cell.
- \( \mathrm{E^\circ_{cell} = 0} \) → equilibrium.
This equation provides a powerful link between thermodynamics, electrochemistry, and spontaneity.
Example :
For a redox reaction transferring 2 electrons, the cell potential is \( \mathrm{E^\circ_{cell} = +0.80\ V} \). Calculate \( \mathrm{\Delta G^\circ} \) and state whether the reaction is spontaneous.
▶️ Answer / Explanation
Step 1: Use \( \mathrm{\Delta G^\circ = -nFE^\circ_{cell}} \).
\( \mathrm{\Delta G^\circ = -(2)(96,485)(0.80) = -154,376\ J = -154.4\ kJ/mol} \)
Step 2: Interpretation:
- \( \mathrm{\Delta G^\circ < 0} \) → spontaneous reaction.
- \( \mathrm{E^\circ_{cell} > 0} \) → galvanic cell (energy produced).
Final Answer: \( \mathrm{\Delta G^\circ = -154.4\ kJ/mol} \), the reaction is spontaneous.
Example :
A redox reaction involving 3 electrons has \( \mathrm{\Delta G^\circ = +261\ kJ/mol} \). Calculate the corresponding \( \mathrm{E^\circ_{cell}} \) and determine whether the reaction is spontaneous.
▶️ Answer / Explanation
Step 1: Rearrange the formula:
\( \mathrm{E^\circ_{cell} = -\dfrac{\Delta G^\circ}{nF}} \)
Step 2: Substitute values:
\( \mathrm{E^\circ_{cell} = -\dfrac{261,000}{(3)(96,485)} = -0.90\ V} \)
Step 3: Interpretation:
- \( \mathrm{E^\circ_{cell} = -0.90\ V} \) → nonspontaneous.
- \( \mathrm{\Delta G^\circ > 0} \) → reaction requires external energy (electrolytic cell).
Final Answer: \( \mathrm{E^\circ_{cell} = -0.90\ V} \); the reaction is nonspontaneous under standard conditions.
