AP Physics 1- 7.3 Representing and Analyzing SHM- Study Notes- New Syllabus

Representing and Analyzing SHM

Displacement in SHM: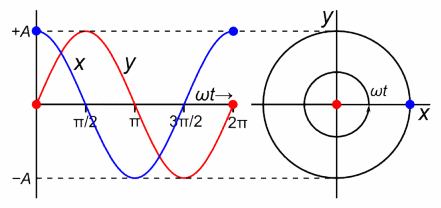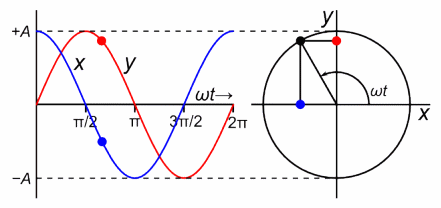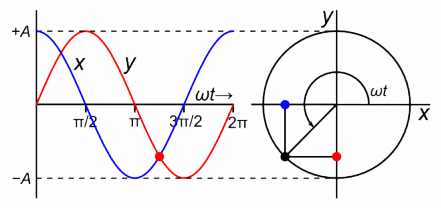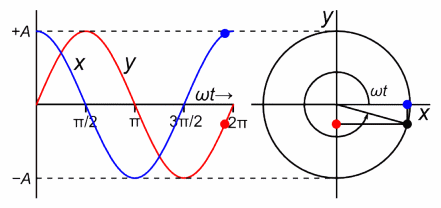

The displacement of an object in SHM from its equilibrium position as a function of time can be represented by:

\( x(t) = A \cos(\omega t + \phi) \) or \( x(t) = A \sin(\omega t + \phi) \)

• \( A \) = amplitude (maximum displacement)
• \( \omega \) = angular frequency (\( \omega = 2 \pi f = \sqrt{\dfrac{k}{m}} \) for mass-spring, \( \omega = \sqrt{\dfrac{g}{L}} \) for pendulum)
• \( \phi \) = phase constant (depends on initial conditions)

Velocity in SHM:

The instantaneous velocity is the time derivative of displacement:

\( v(t) = \dfrac{dx}{dt} = – A \omega \sin(\omega t + \phi) \)

Maximum velocity: \( v_{max} = A \omega \)

Acceleration in SHM:

The instantaneous acceleration is the time derivative of velocity or second derivative of displacement:

\( a(t) = \dfrac{dv}{dt} = \dfrac{d^2 x}{dt^2} = – A \omega^2 \cos(\omega t + \phi) = – \omega^2 x(t) \)

Maximum acceleration: \( a_{max} = A \omega^2 \)

Minima, Maxima, and Zeros:

• Displacement: maximum at \( \pm A \), zero at equilibrium.
• Velocity: maximum at equilibrium, zero at maximum displacement (\( \pm A \)).
• Acceleration: maximum at maximum displacement (\( \pm A \)), zero at equilibrium.

Recognizing these extrema or zeros helps in qualitatively describing the behavior of the SHM.

Key Relationships: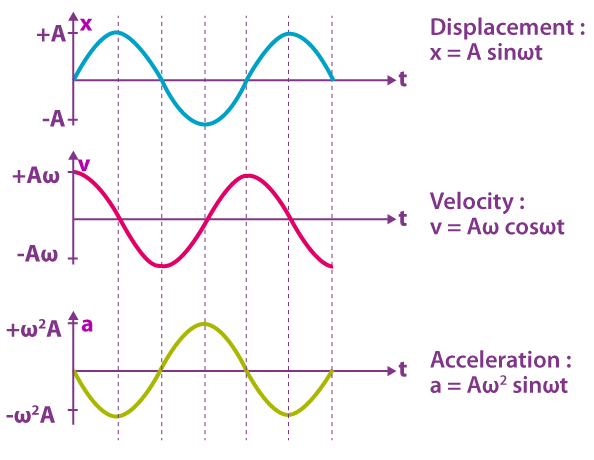

• Acceleration is always proportional and opposite to displacement: \( a \propto -x \)
• Velocity is maximum at the equilibrium position and zero at maximum displacement
• Acceleration is maximum at maximum displacement and zero at the equilibrium position

Graphical Representation:

• Displacement-time graph: Cosine or sine wave; amplitude = maximum displacement
• Velocity-time graph: Sine or cosine wave, shifted by 90° relative to displacement
• Acceleration-time graph: Sine or cosine wave, shifted by 180° relative to displacement