Resistive Forces AP Physics C Mechanics MCQ – Exam Style Questions etc.
Resistive Forces AP Physics C Mechanics MCQ
Unit 2: Force and Translational Dynamics
Weightage : 20-15%
Question 1
A resistive force acts on a moving object such that \( \mathrm{F_r = -k v} \). If the object has an initial velocity \( \mathrm{v_0} \), what is the correct expression for its velocity as a function of time?
(A) \( \mathrm{v = v_0 + k t / m} \)
(B) \( \mathrm{v = v_0 e^{-k t / m}} \)
(C) \( \mathrm{v = v_0 e^{k t / m}} \)
(D) \( \mathrm{v = v_0 – k t / m} \)
▶️ Answer/Explanation
Start with Newton: \( \mathrm{m \dfrac{dv}{dt} = -k v} \).
Separate variables: \( \mathrm{\dfrac{dv}{v} = -\dfrac{k}{m} dt} \) and integrate both sides.
Integration gives \( \mathrm{\ln|v| = -\dfrac{k}{m} t + C} \); apply \( \mathrm{v(0)=v_0} \) to get \( \mathrm{C=\ln v_0} \).
Exponentiate to obtain \( \mathrm{v(t)=v_0 e^{-k t / m}} \).
Correct answer: (B)
Question 2
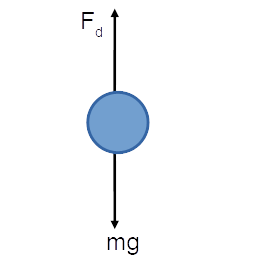
At \( \mathrm{t = 0} \), an object starts from rest and falls under gravity with air resistance \( \mathrm{F_d = -k v} \). What is the velocity at time \( t \)?
(A) \( \mathrm{v = g t} \)
(B) \( \mathrm{v = \dfrac{mg}{k} (1 – e^{-k t / m})} \)
(C) \( \mathrm{v = \dfrac{k g}{m} e^{-k t / m}} \)
(D) \( \mathrm{v = g e^{-m t / k}} \)
▶️ Answer/Explanation
Equation of motion: \( \mathrm{m \dfrac{dv}{dt} = mg – k v} \).
This linear ODE has integrating factor solution or you can use known form:
\( \mathrm{v(t)=v_t(1-e^{-k t/m})} \) where \( \mathrm{v_t=\dfrac{mg}{k}} \).
Substitute \( \mathrm{v_t} \) to get \( \mathrm{v(t)=\dfrac{mg}{k}\big(1-e^{-k t/m}\big)} \).
This starts at 0 and asymptotically approaches \( \mathrm{mg/k} \).
Correct answer: (B)
Question 3
An object with mass \( \mathrm{m} \) and initial speed \( \mathrm{v_0} \) moves under \( \mathrm{F_r = -k v} \). What is the time required for the object to travel half of its maximum possible distance \( \mathrm{x_{max}=\dfrac{m v_0}{k}} \)?
(A) \( \mathrm{t = \dfrac{m}{k} \ln 2} \)
(B) \( \mathrm{t = \dfrac{m}{k} \ln(1/2)} \)
(C) \( \mathrm{t = -\dfrac{m}{k} \ln(1/2)} \)
(D) \( \mathrm{t = \dfrac{m}{k} \ln(1 – 1/2)} \)
▶️ Answer/Explanation
Position: \( \mathrm{x(t)=\dfrac{m v_0}{k}\big(1-e^{-k t/m}\big)} \) and \( \mathrm{x_{max}=\dfrac{m v_0}{k}} \).
Set \( \mathrm{x(t)}=\tfrac{1}{2}\mathrm{x_{max}} \Rightarrow 1-e^{-k t/m} = \tfrac{1}{2} \). So \( e^{-k t/m} = \tfrac{1}{2} \Rightarrow -\dfrac{k t}{m} = \ln\!\tfrac{1}{2} \).
Thus \( t = -\dfrac{m}{k}\ln\!\tfrac{1}{2} = \dfrac{m}{k}\ln 2 \).
Correct answer: (A)
