AP Precalculus -1.10 Rational Functions and Holes- Study Notes - Effective Fall 2023
AP Precalculus -1.10 Rational Functions and Holes- Study Notes – Effective Fall 2023
AP Precalculus -1.10 Rational Functions and Holes- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Determine holes in graphs of rational functions.
Key Concepts:
- Holes in the Graph of a Rational Function
- Determining the Location of a Hole Using Limits
Holes in the Graph of a Rational Function
Let a rational function be written as
\( r(x) = \dfrac{p(x)}{q(x)} \)
Suppose \( a \) is a real zero of both the numerator and the denominator.
If the multiplicity of \( a \) as a real zero in the numerator is greater than or equal to its multiplicity as a real zero in the denominator, then the graph of the rational function has a hole at the corresponding input value \( x = a \).
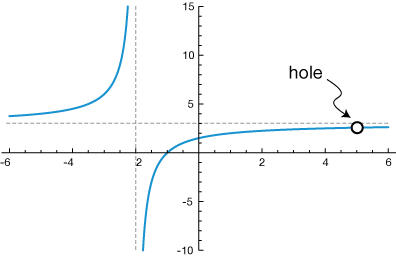
This occurs because all factors of \( (x – a) \) in the denominator cancel when the function is simplified.
Although the simplified expression is defined at \( x = a \), the original rational function is not defined at that value.
As a result, the graph has a removable discontinuity, called a hole, rather than a vertical asymptote.
The hole occurs at the point \( (a, y) \), where \( y \) is the value obtained by evaluating the simplified function at \( x = a \).
Example:
Determine whether the rational function has a hole or a vertical asymptote at \( x = 2 \):
\( r(x) = \dfrac{(x – 2)^2}{(x – 2)} \)
▶️ Answer/Explanation
The multiplicity of \( x = 2 \) in the numerator is 2.
The multiplicity of \( x = 2 \) in the denominator is 1.
Since the multiplicity in the numerator is greater, the factor cancels completely.
After simplification:
\( r(x) = x – 2 \), for \( x \ne 2 \)
Evaluate the simplified function at \( x = 2 \):
\( y = 0 \)
Conclusion
The graph has a hole at \( (2, 0) \).
Example:
Analyze the behavior at \( x = -1 \) for the rational function
\( f(x) = \dfrac{(x + 1)^3}{(x + 1)^2} \)
▶️ Answer/Explanation
The multiplicity of \( x = -1 \) in the numerator is 3.
The multiplicity of \( x = -1 \) in the denominator is 2.
All factors of \( (x + 1) \) in the denominator cancel.
After simplification:
\( f(x) = x + 1 \), for \( x \ne -1 \)
Evaluate the simplified function at \( x = -1 \):
\( y = 0 \)
Conclusion
The graph has a hole at \( (-1, 0) \).
Determining the Location of a Hole Using Limits
Let \( r(x) \) be a rational function.
If the graph of \( r(x) \) has a hole at \( x = c \), then the function is not defined at \( x = c \), but the output values for inputs sufficiently close to \( c \) approach a single finite value.
If input values near \( c \) correspond to output values that are arbitrarily close to \( L \), then the hole is located at the point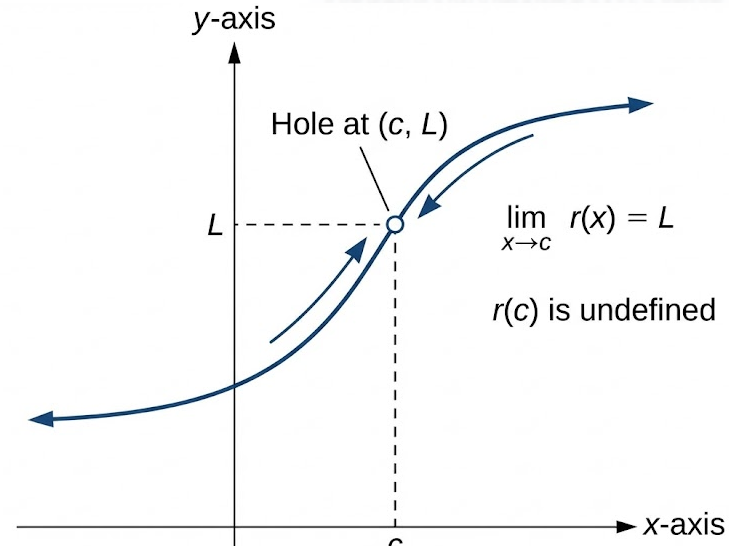
\( (c, L) \)
This behavior is described using limits:
\( \lim_{x \to c} r(x) = L \)
For a hole to exist, the left-hand limit and the right-hand limit must both exist and be equal:
\( \lim_{x \to c^-} r(x) = \lim_{x \to c^+} r(x) = \lim_{x \to c} r(x) = L \)
Although the limit exists, the function value \( r(c) \) is undefined, which creates the hole.
Example:
Find the location of the hole in the graph of
\( r(x) = \dfrac{x^2 – 1}{x – 1} \)
▶️ Answer/Explanation
Factor the numerator:
\( x^2 – 1 = (x – 1)(x + 1) \)
Cancel the common factor:
\( r(x) = x + 1 \), for \( x \ne 1 \)
Evaluate the limit:
\( \lim_{x \to 1} r(x) = 1 + 1 = 2 \)
Conclusion
The graph has a hole at \( (1, 2) \).
Example:
Determine the location of the hole in the graph of
\( f(x) = \dfrac{(x + 2)(x – 3)}{x + 2} \)
▶️ Answer/Explanation
Cancel the common factor \( (x + 2) \):
\( f(x) = x – 3 \), for \( x \ne -2 \)
Evaluate the limit:
\( \lim_{x \to -2} f(x) = -2 – 3 = -5 \)
Conclusion
The graph has a hole at \( (-2, -5) \).
