AP Precalculus -1.12 Transformations of Functions- Study Notes - Effective Fall 2023
AP Precalculus -1.12 Transformations of Functions- Study Notes – Effective Fall 2023
AP Precalculus -1.12 Transformations of Functions- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Construct a function that is an additive and/or multiplicative transformation of another function.
Key Concepts:
Additive Transformations (Vertical Translations)
Additive Transformations (Horizontal Translations)
Multiplicative Transformations (Vertical Dilations and Reflections)
Multiplicative Transformations (Horizontal Dilations and Reflections)
Combined Additive and Multiplicative Transformations
Effect of Transformations on Domain and Range
Additive Transformations (Vertical Translations)
An additive transformation changes a function by adding a constant to its output.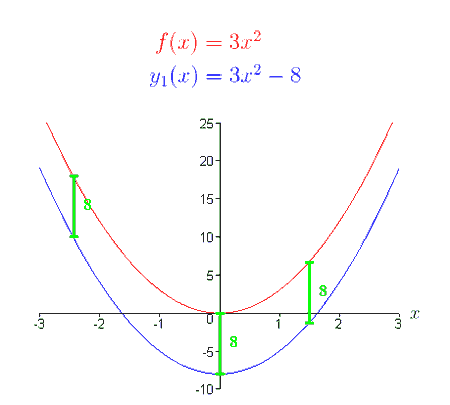
If a function \( \mathrm{f(x)} \) is transformed into a new function
\( \mathrm{ \displaystyle g(x) = f(x) + k } \)
then the graph of \( \mathrm{f(x)} \) is translated vertically by \( \mathrm{k} \) units.
Effect of the Value of \( \mathrm{k} \)
• If \( \mathrm{k > 0} \), the graph shifts upward by \( \mathrm{k} \) units
• If \( \mathrm{k < 0} \), the graph shifts downward by \( \mathrm{|k|} \) units
A vertical translation does not change the shape of the graph, its domain, or its horizontal features. It only changes the output values.
All y-values increase or decrease by the same amount.
Example :
Let
\( \mathrm{ \displaystyle f(x) = x^2 } \)
Define a new function
\( \mathrm{ \displaystyle g(x) = f(x) + 3 } \)
Describe the transformation.
▶️ Answer/Explanation
Substitute \( \mathrm{f(x)} \):
\( \mathrm{ \displaystyle g(x) = x^2 + 3 } \)
Every output value of \( \mathrm{f(x)} \) increases by 3.
Conclusion
The graph of \( \mathrm{f(x)} \) is shifted upward by 3 units.
Example :
Let
\( \mathrm{ \displaystyle f(x) = \dfrac{1}{x} } \)
Define
\( \mathrm{ \displaystyle g(x) = f(x) – 2 } \)
Describe the effect on the graph.
▶️ Answer/Explanation
Substitute \( \mathrm{f(x)} \):
\( \mathrm{ \displaystyle g(x) = \dfrac{1}{x} – 2 } \)
Every output value decreases by 2.
Conclusion
The graph is shifted downward by 2 units.
The vertical asymptote remains at \( \mathrm{x = 0} \), but the horizontal asymptote shifts to \( \mathrm{y = -2} \).
Additive Transformations (Horizontal Translations)
An additive transformation inside the input changes a function by adding a constant to the input variable.
If a function \( \mathrm{f(x)} \) is transformed into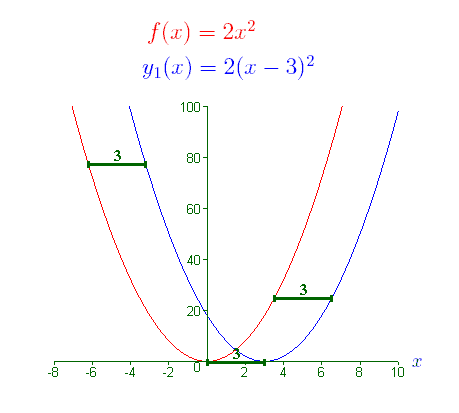
\( \mathrm{ \displaystyle g(x) = f(x + h) } \)
then the graph of \( \mathrm{f(x)} \) undergoes a horizontal translation by \( \mathrm{-h} \) units.
Important Direction Rule
Horizontal shifts move in the opposite direction of the sign inside the function.
• If \( \mathrm{h > 0} \), the graph shifts left by \( \mathrm{h} \) units
• If \( \mathrm{h < 0} \), the graph shifts right by \( \mathrm{|h|} \) units
A horizontal translation does not change the shape of the graph or the output values themselves. It only changes which input values produce those outputs.
All key features such as intercepts, asymptotes, and turning points move horizontally by the same amount.
Example :
Let
\( \mathrm{ \displaystyle f(x) = x^2 } \)
Define a new function
\( \mathrm{ \displaystyle g(x) = f(x + 4) } \)
Describe the transformation.
▶️ Answer/Explanation
Substitute \( \mathrm{f(x)} \):
\( \mathrm{ \displaystyle g(x) = (x + 4)^2 } \)
The \( \mathrm{+4} \) inside the function causes a shift to the left.
Conclusion
The graph of \( \mathrm{f(x)} \) is translated 4 units to the left.
Example :
Let
\( \mathrm{ \displaystyle f(x) = \dfrac{1}{x} } \)
Define
\( \mathrm{ \displaystyle g(x) = f(x – 2) } \)
Describe the effect on the graph.
▶️ Answer/Explanation
Substitute \( \mathrm{f(x)} \):
\( \mathrm{ \displaystyle g(x) = \dfrac{1}{x – 2} } \)
The \( \mathrm{-2} \) inside the function causes a shift to the right.
Conclusion
The graph is translated 2 units to the right.
The vertical asymptote shifts from \( \mathrm{x = 0} \) to \( \mathrm{x = 2} \).
Multiplicative Transformations (Vertical Dilations and Reflections)
A multiplicative transformation changes a function by multiplying its output values by a nonzero constant.
If a function \( \mathrm{f(x)} \) is transformed into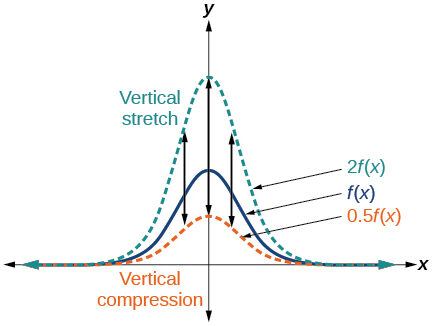
\( \mathrm{ \displaystyle g(x) = a f(x), \; a \ne 0 } \)
then the graph of \( \mathrm{f(x)} \) undergoes a vertical dilation by a factor of \( \mathrm{|a|} \).
Effect of the Value of \( \mathrm{a} \)
• If \( \mathrm{|a| > 1} \), the graph is stretched vertically
• If \( \mathrm{0 < |a| < 1} \), the graph is compressed vertically
If \( \mathrm{a < 0} \), the transformation also includes a reflection over the x-axis.
A vertical dilation does not change the x-values of key features such as intercepts or asymptotes. It only affects the y-values.
Example :
Let
\( \mathrm{ \displaystyle f(x) = x^2 } \)
Define a new function
\( \mathrm{ \displaystyle g(x) = 3f(x) } \)
Describe the transformation.
▶️ Answer/Explanation
Substitute \( \mathrm{f(x)} \):
\( \mathrm{ \displaystyle g(x) = 3x^2 } \)
Since \( \mathrm{|a| = 3 > 1} \), the graph is stretched vertically.
Conclusion
The graph of \( \mathrm{f(x)} \) is vertically stretched by a factor of 3.
Example :
Let
\( \mathrm{ \displaystyle f(x) = \sqrt{x} } \)
Define
\( \mathrm{ \displaystyle g(x) = -\dfrac{1}{2} f(x) } \)
Describe the transformation.
▶️ Answer/Explanation
Substitute \( \mathrm{f(x)} \):
\( \mathrm{ \displaystyle g(x) = -\dfrac{1}{2}\sqrt{x} } \)
The factor \( \mathrm{|a| = \dfrac{1}{2}} \) causes a vertical compression.
The negative sign reflects the graph over the x-axis.
Conclusion
The graph is vertically compressed by a factor of \( \mathrm{\dfrac{1}{2}} \) and reflected over the x-axis.
Multiplicative Transformations (Horizontal Dilations and Reflections)
A multiplicative transformation inside the input changes a function by multiplying the input variable by a nonzero constant.
If a function \( \mathrm{f(x)} \) is transformed into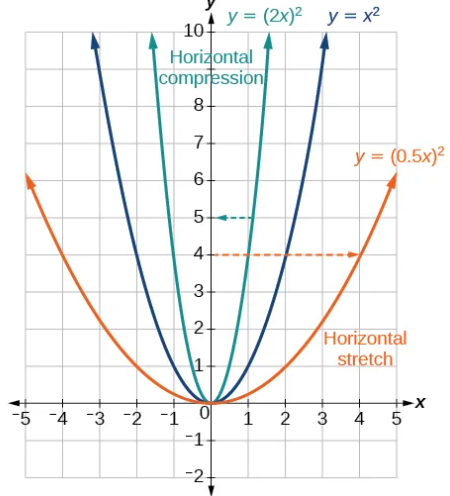
\( \mathrm{ \displaystyle g(x) = f(bx), \; b \ne 0 } \)
then the graph of \( \mathrm{f(x)} \) undergoes a horizontal dilation by a factor of
\( \mathrm{ \left| \dfrac{1}{b} \right| } \)
Important Direction and Scale Rules
• If \( \mathrm{|b| > 1} \), the graph is horizontally compressed
• If \( \mathrm{0 < |b| < 1} \), the graph is horizontally stretched
If \( \mathrm{b < 0} \), the transformation also includes a reflection over the y-axis.
Horizontal dilations change the x-values of key features such as intercepts, asymptotes, and turning points, but do not change the y-values themselves.
Example :
Let
\( \mathrm{ \displaystyle f(x) = x^2 } \)
Define
\( \mathrm{ \displaystyle g(x) = f(2x) } \)
Describe the transformation.
▶️ Answer/Explanation
Substitute \( \mathrm{f(x)} \):
\( \mathrm{ \displaystyle g(x) = (2x)^2 = 4x^2 } \)
The value \( \mathrm{|b| = 2} \) gives a horizontal scale factor of
\( \mathrm{ \left| \dfrac{1}{2} \right| } \)
Conclusion
The graph of \( \mathrm{f(x)} \) is horizontally compressed by a factor of \( \mathrm{\dfrac{1}{2}} \).
Example :
Let
\( \mathrm{ \displaystyle f(x) = \sqrt{x} } \)
Define
\( \mathrm{ \displaystyle g(x) = f(-\tfrac{1}{2}x) } \)
Describe the transformation.
▶️ Answer/Explanation
The value \( \mathrm{b = -\tfrac{1}{2}} \) gives a horizontal scale factor of
\( \mathrm{ \left| \dfrac{1}{-\tfrac{1}{2}} \right| = 2 } \)
The negative sign causes a reflection over the y-axis.
Conclusion
The graph is horizontally stretched by a factor of 2 and reflected over the y-axis.
Combined Additive and Multiplicative Transformations
Additive and multiplicative transformations can be applied together to a function.
When combined, these transformations result in a mixture of horizontal and vertical translations, dilations, and possibly reflections.
A general transformed function can be written as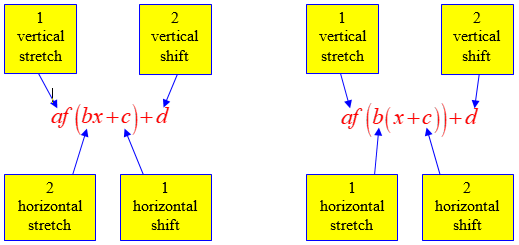
\( \mathrm{ \displaystyle g(x) = a\,f(bx + h) + k } \)
Meaning of Each Parameter
• \( \mathrm{a} \): vertical dilation by factor \( \mathrm{|a|} \); reflection over the x-axis if \( \mathrm{a < 0} \)
• \( \mathrm{b} \): horizontal dilation by factor \( \mathrm{\left|\dfrac{1}{b}\right|} \); reflection over the y-axis if \( \mathrm{b < 0} \)
• \( \mathrm{h} \): horizontal translation by \( \mathrm{-h} \) units
• \( \mathrm{k} \): vertical translation by \( \mathrm{k} \) units
These transformations do not change the fundamental shape of the graph, but they change its position, orientation, and scale.
Example :
Let
\( \mathrm{ \displaystyle f(x) = x^2 } \)
Define
\( \mathrm{ \displaystyle g(x) = 2f(x – 3) + 1 } \)
Describe the transformations.
▶️ Answer/Explanation
Rewrite the function:
\( \mathrm{ \displaystyle g(x) = 2(x – 3)^2 + 1 } \)
Transformations applied:
• Shift right 3 units
• Vertical stretch by factor 2
• Shift up 1 unit
Conclusion
The graph is repositioned and stretched, but remains a parabola.
Example :
Let
\( \mathrm{ \displaystyle f(x) = \dfrac{1}{x} } \)
Define
\( \mathrm{ \displaystyle g(x) = -f(2x + 4) – 3 } \)
Describe the transformations.
▶️ Answer/Explanation
Rewrite the function:
\( \mathrm{ \displaystyle g(x) = -\dfrac{1}{2x + 4} – 3 } \)
Transformations applied:
• Horizontal compression by factor \( \mathrm{\dfrac{1}{2}} \)
• Reflection over the x-axis
• Shift down 3 units
Conclusion
The graph undergoes multiple transformations while preserving its rational shape.
Effect of Transformations on Domain and Range
When a function is transformed from a parent function, its domain and range may change depending on the type of transformation applied.
Some transformations change only the position or scale of the graph, while others change the set of allowable input or output values.
General Rules
• Vertical translations and dilations affect the range but do not change the domain
• Horizontal translations and dilations affect the domain and may affect the range
• Reflections preserve both domain and range but may change the direction of outputs
Restrictions present in the parent function, such as square roots or denominators, move with the transformation.
Example :
The parent function is
\( \mathrm{ \displaystyle f(x) = \sqrt{x} } \)
The domain is \( \mathrm{x \ge 0} \) and the range is \( \mathrm{y \ge 0} \).
Now consider the transformation
\( \mathrm{ \displaystyle g(x) = \sqrt{x – 3} + 2 } \)
▶️ Answer/Explanation
Domain
Require \( \mathrm{x – 3 \ge 0} \), so \( \mathrm{x \ge 3} \).
Range
Since the graph is shifted up by 2 units, the range becomes \( \mathrm{y \ge 2} \).
Conclusion
Both the domain and range are different from those of the parent function.
Example :
The parent function is
\( \mathrm{ \displaystyle f(x) = \dfrac{1}{x} } \)
The domain is \( \mathrm{x \ne 0} \) and the range is \( \mathrm{y \ne 0} \).
Now consider the transformation
\( \mathrm{ \displaystyle g(x) = \dfrac{1}{x – 2} + 1 } \)
▶️ Answer/Explanation
Domain
The denominator cannot be zero, so \( \mathrm{x – 2 \ne 0} \), which gives \( \mathrm{x \ne 2} \).
Range
The vertical shift moves the horizontal asymptote from \( \mathrm{y = 0} \) to \( \mathrm{y = 1} \), so \( \mathrm{y \ne 1} \).
Conclusion
The domain and range have both changed due to the transformation.
