AP Precalculus -1.13 Function Models: Selection and Assumptions- Study Notes - Effective Fall 2023
AP Precalculus -1.13 Function Models: Selection and Assumptions- Study Notes – Effective Fall 2023
AP Precalculus -1.13 Function Models: Selection and Assumptions- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Identify an appropriate function type to construct a function model for a given scenario.
Describe assumptions and restrictions related to building a function model.
Key Concepts:
- Identifying an Appropriate Function Type for a Given Scenario
- Assumptions and Restrictions in Function Modeling
Identifying an Appropriate Function Type for a Given Scenario
When modeling a real-world scenario or data set, the choice of function type depends on how the input and output quantities vary together.
Mathematical expressions help justify why a particular model is appropriate by describing the underlying pattern of change.
Linear Functions
Linear functions are appropriate when the rate of change is approximately constant.
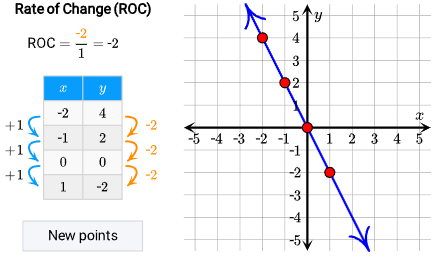
Mathematically, a constant rate of change means
\( \mathrm{ \displaystyle \dfrac{f(x_2) – f(x_1)}{x_2 – x_1} = m } \)
for all input values, where \( \mathrm{m} \) is constant.
The general linear model is
\( \mathrm{ \displaystyle f(x) = mx + b } \)
Quadratic Functions
Quadratic functions are used when the rate of change varies linearly, meaning the first differences are not constant but the second differences are.
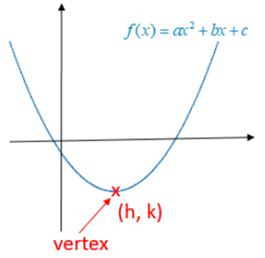
This is expressed numerically as
\( \mathrm{ \displaystyle \Delta^2 f(x) = \text{constant} } \)
The general quadratic model is
\( \mathrm{ \displaystyle f(x) = ax^2 + bx + c } \)
Quadratic graphs are symmetric and have a single maximum or minimum.
Geometric Contexts
In geometric modeling, the number of dimensions often determines the degree of the polynomial.
For area-based contexts (two dimensions):
\( \mathrm{ \displaystyle A(x) = kx^2 } \)
For volume-based contexts (three dimensions):
\( \mathrm{ \displaystyle V(x) = kx^3 } \)
Here, \( \mathrm{k} \) is a constant determined by the shape of the object.
Polynomial Functions with Multiple Features
Polynomial functions are appropriate when a scenario involves multiple real zeros or multiple turning points.
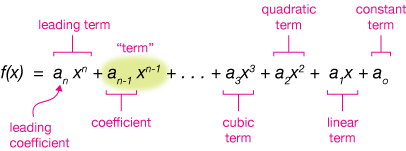
A general polynomial model is
\( \mathrm{ \displaystyle f(x) = a_n x^n + a_{n-1} x^{n-1} + \dots + a_1 x + a_0 } \)
A polynomial of degree \( \mathrm{n} \) can have up to \( \mathrm{n} \) real zeros and up to \( \mathrm{n-1} \) local extrema.
Constant nth Differences
If a data set has constant nonzero nth differences, then it can be modeled by a polynomial of degree \( \mathrm{n} \).
Symbolically, this is expressed as
\( \mathrm{ \displaystyle \Delta^n f(x) = \text{constant}, \; \Delta^{n-1} f(x) \ne \text{constant} } \)
Modeling a Finite Set of Points
A polynomial function of degree \( \mathrm{n} \) or less can be constructed to pass exactly through \( \mathrm{n+1} \) points with distinct input values.
This can be represented conceptually as
\( \mathrm{ \displaystyle f(x_i) = y_i \quad \text{for } i = 1,2,\dots,n+1 } \)
Piecewise-Defined Functions
When a scenario exhibits different behaviors on different intervals, a piecewise-defined function is appropriate.
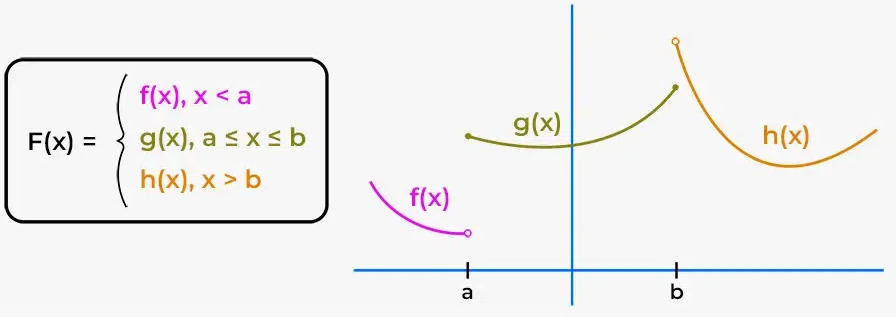
A general piecewise model is written as
\( \mathrm{ \displaystyle f(x) = \begin{cases} f_1(x), & x_1 \le x < x_2 \\ f_2(x), & x_2 \le x < x_3 \\ \vdots \end{cases} } \)
Each formula models the behavior of the scenario on its corresponding interval.
Selecting the correct function type ensures that the mathematical model accurately reflects the structure of the situation being studied.
Example
A cyclist travels at a steady speed, covering 12 kilometers every hour.
Which type of function is most appropriate to model the distance traveled as a function of time, and why?
▶️ Answer/Explanation
The distance increases at a constant rate, so a linear function is appropriate.
\( \mathrm{ \displaystyle d(t) = 12t } \)
Example
The height of a firework rises, slows down, reaches a maximum height, and then falls back to the ground.
Which type of function best models the height as a function of time?
▶️ Answer/Explanation
The motion is symmetric with a single maximum, so a quadratic function is appropriate.
\( \mathrm{ \displaystyle h(t) = at^2 + bt + c } \)
Example
The area of a circular garden depends on the radius of the garden.
Which type of function should be used to model the area in terms of the radius?
▶️ Answer/Explanation
Area is a two-dimensional quantity, so a quadratic model is appropriate.
\( \mathrm{ \displaystyle A(r) = \pi r^2 } \)
Example
A profit function crosses the horizontal axis three times and has two turning points.
Which type of function is suitable for modeling this situation?
▶️ Answer/Explanation
Multiple real zeros and multiple extrema suggest a higher-degree polynomial model.
\( \mathrm{ \displaystyle f(x) = a_3x^3 + a_2x^2 + a_1x + a_0 } \)
Example
A table of values has constant third differences.
What type of function should be used to model the data?
▶️ Answer/Explanation
Constant third differences indicate a polynomial of degree 3.
\( \mathrm{ \displaystyle f(x) = ax^3 + bx^2 + cx + d } \)
Example
Four data points with distinct x-values are given from an experiment.
What is the highest degree polynomial needed to model the data exactly?
▶️ Answer/Explanation
A polynomial of degree at most 3 can pass through four distinct points.
\( \mathrm{ \displaystyle f(x_i) = y_i,\; i=1,2,3,4 } \)
Example
A phone plan charges one rate for the first 2 GB of data and a different rate after that.
Which type of function best models the total cost?
▶️ Answer/Explanation
Different rules apply on different intervals, so a piecewise-defined function is appropriate.
\( \mathrm{ \displaystyle C(x)= \begin{cases} f_1(x), & 0 \le x \le 2 \\ f_2(x), & x > 2 \end{cases} } \)
Assumptions and Restrictions in Function Modeling
When building a function model for a real-world scenario or data set, it is important to clearly identify the assumptions being made and any necessary restrictions on the model.
Assumptions simplify reality so that the situation can be represented mathematically, while restrictions ensure that the model remains meaningful in context.
Consistency Assumptions
A function model often assumes that certain aspects of the situation remain consistent throughout the interval being modeled.
For example, a linear model assumes that the rate of change does not vary:
\( \mathrm{ \displaystyle \dfrac{f(x_2)-f(x_1)}{x_2-x_1} = m,\; \text{constant} } \)
Such an assumption may ignore real-world effects like friction, fatigue, or external forces that could cause the rate to change.
Assumptions About How Quantities Change Together
A model also assumes a specific relationship between the input and output variables.
For instance, choosing a quadratic model assumes that the rate of change itself varies linearly:
\( \mathrm{ \displaystyle \Delta^2 f(x) = \text{constant} } \)
If the actual relationship between variables is more complex, the model may only be an approximation.
Domain Restrictions
A function model may require restrictions on the domain so that only meaningful input values are included.
Domain restrictions can arise from:
• Mathematical constraints, such as square roots or denominators
• Contextual constraints, such as time, distance, or quantity limits
• Extreme or unrealistic values suggested by the data
For example, if a model involves a square root:
\( \mathrm{ \displaystyle f(x) = \sqrt{x-2} } \)
then the domain must satisfy
\( \mathrm{ \displaystyle x \ge 2 } \)
Range Restrictions
In some situations, the range of a function model must also be restricted.
Range restrictions may be required due to:
• Physical limitations, such as nonnegative height, distance, or population
• Contextual meaning, such as whole-number outputs
• Rounding or measurement constraints
For example, if a model represents the number of people:
\( \mathrm{ \displaystyle P(t) = 2.4t + 10 } \)
the range may be restricted to whole numbers:
\( \mathrm{ \displaystyle P(t) \in \mathbb{Z}_{\ge 0} } \)
Clearly stating assumptions and restrictions helps ensure that a function model is interpreted correctly and used only within its intended limits.
Example
A company models the total cost of producing items using the function
\( \mathrm{ \displaystyle C(x) = 15x + 200 } \)
where \( \mathrm{x} \) is the number of items produced.
Describe one assumption made by this model.
▶️ Answer/Explanation
The model assumes that the cost per item is constant and does not change as production increases.
Example
The height of an object is modeled by a quadratic function of time.
What assumption is being made about how height and time change together?
▶️ Answer/Explanation
The model assumes that the rate of change of height varies linearly with time.
Example
A function is used to model the distance a runner travels:
\( \mathrm{ \displaystyle d(t) = 6t } \)
Explain a reasonable restriction on the domain of this model.
▶️ Answer/Explanation
Time cannot be negative, so the domain should be restricted to \( \mathrm{t \ge 0} \).
Example
The function
\( \mathrm{ \displaystyle f(x) = \sqrt{x – 5} } \)
is used to model a real-world quantity.
Identify the domain restriction and explain its source.
▶️ Answer/Explanation
The expression under the square root must be nonnegative, so the domain is \( \mathrm{x \ge 5} \).
Example
A population model gives
\( \mathrm{ \displaystyle P(t) = 1200 + 35t } \)
What restriction should be placed on the range of this model, and why?
▶️ Answer/Explanation
Population values should be whole numbers and nonnegative, so the range should be restricted to nonnegative integers.
Example
A polynomial model predicts negative revenue values for very large input values.
Explain why the model may need a restricted domain.
▶️ Answer/Explanation
Negative revenue may not be meaningful in context, so the domain should be limited to realistic input values based on the situation.
