AP Precalculus -1.3 Rates of Change in Linear and Quadratic Functions- MCQ Exam Style Questions - Effective Fall 2023
AP Precalculus -1.3 Rates of Change in Linear and Quadratic Functions- MCQ Exam Style Questions – Effective Fall 2023
AP Precalculus -1.3 Rates of Change in Linear and Quadratic Functions- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.
Question
(B) \( g \)
(C) \( h \)
(D) \( k \)
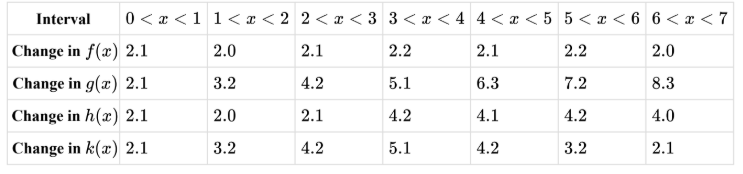
▶️ Answer/Explanation
For a piecewise-linear function with two linear segments, the average rate of change should be roughly constant in each segment but different between segments.
- \( f \): rates ~constant ⇒ one linear function, not two segments.
- \( g \): rates increase steadily ⇒ curved, not piecewise-linear.
- \( h \): rates ~2.1 for intervals 1–3 (0<x<3), then ~4.2 for intervals 4–7 (3<x<7) ⇒ two different constant slopes ⇒ piecewise-linear with two segments.
- \( k \): rates increase then decrease ⇒ not constant in two blocks.
✅ Answer: (C)
Question
(B) The average rate of change of \( f \) over consecutive equal-length input-value intervals is positive, so the graph of \( f \) could be a parabola that opens up.
(C) The average rate of change of \( f \) over consecutive equal-length input-value intervals is increasing at a constant rate, so the graph of \( f \) could be a line with a positive slope.
(D) The average rate of change of \( f \) over consecutive equal-length input-value intervals is increasing at a constant rate, so the graph of \( f \) could be a parabola that opens up.
▶️ Answer/Explanation
Average rate of change from \( a \) to \( a+1 \) is \( 2a + 1 \), which is linear in \( a \).
If \( f \) were linear, the average rate of change would be constant (not depend on \( a \)), so (A) and (C) are false.
If \( f \) is quadratic, then the average rate of change over a 1-unit interval is indeed linear in \( a \) (this can be derived). Here \( 2a + 1 \) increases as \( a \) increases, at a constant rate (slope 2 with respect to \( a \)), meaning \( f \) is concave up (opens upward).
Thus the correct reasoning: the average rate of change is increasing at a constant rate ⇒ \( f \) could be a parabola opening up.
✅ Answer: (D)
Question
| \( x \) | -3 | 3 | 6 |
|---|---|---|---|
| \( f(x) \) | -10 | -2 | 2 |
(B) \(\frac{29}{4}\)
(C) \(\frac{28}{3}\)
(D) \(\frac{34}{3}\)
▶️ Answer/Explanation
Using points (3, -2) and (6, 2): slope \( m = \frac{2 – (-2)}{6 – 3} = \frac{4}{3} \).
Equation: \( f(x) – (-2) = \frac{4}{3}(x – 3) \) ⇒ \( f(x) = \frac{4}{3}x – 4 – 2 = \frac{4}{3}x – 6 \).
Check with (-3, -10): \( \frac{4}{3}(-3) – 6 = -4 – 6 = -10 \) ✓.
Now \( f(13) = \frac{4}{3}(13) – 6 = \frac{52}{3} – \frac{18}{3} = \frac{34}{3} \).
✅ Answer: (D)
Question
(B) 3
(C) 5
(D) The average rate of change on the interval \( 6 \leq x \leq 8 \) cannot be determined from the information given.
▶️ Answer/Explanation
For a quadratic function \( p(x) = ax^2 + bx + c \), the average rate of change over equal-length intervals changes linearly.
Given:
Average rate on \( [0,2] \) is \( -4 \).
Average rate on \( [2,4] \) is \( -1 \).
The change from one interval to the next is constant: \( -1 – (-4) = 3 \).
Thus, for each subsequent interval of length 2, the average rate increases by 3.
Sequence of average rates:
\( [0,2]: -4 \)
\( [2,4]: -1 \)
\( [4,6]: -1 + 3 = 2 \)
\( [6,8]: 2 + 3 = 5 \)
✅ Answer: (C) 5
Question
(B) The rate of change of the rates of change is 0 meters per second per second, and the object is neither speeding up nor slowing down.
(C) The rate of change of the rates of change is 4 meters per second, and the object is neither speeding up nor slowing down.
(D) The rate of change of the rates of change is 4 meters per second per second, and the object is speeding up.
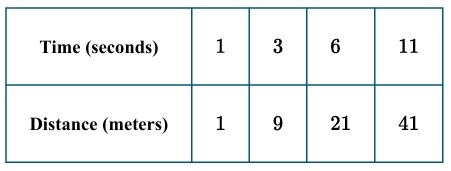
▶️ Answer/Explanation
Calculate the average rate of change (speed) over each time interval:
From \( t=1 \) to \( t=3 \): \( \frac{9-1}{3-1} = \frac{8}{2} = 4 \) m/s
From \( t=3 \) to \( t=6 \): \( \frac{21-9}{6-3} = \frac{12}{3} = 4 \) m/s
From \( t=6 \) to \( t=11 \): \( \frac{41-21}{11-6} = \frac{20}{5} = 4 \) m/s
The speed is constant at 4 m/s, so the acceleration (rate of change of speed) is 0 m/s².
Therefore, the rate of change of the rates of change is \( 0 \) m/s², and the object moves with constant speed (neither speeding up nor slowing down).
✅ Answer: (B)
Question
The table gives values of a function \(f\) for selected values of \(x\). Which of the following conclusions with reason is consistent with the data in the table?
(B) \(f\) could be a linear function because the rates of change over consecutive equal-length intervals in the table can be described by \(y = 2x + 1\).
(C) \(f\) could be a quadratic function because the rates of change over consecutive equal-length intervals in the table can be described by \(y = 2x\).
(D) \(f\) could be a quadratic function because the rates of change over consecutive equal-length intervals in the table can be described by \(y = 2x + 1\).
▶️ Answer/Explanation
\(
\begin{array}{c|cccc}
x & -2 & -1 & 0 & 1 \\
\hline
f(x) & 5 & 2 & 1 & 2
\end{array}
\)
Step 1: Rates of change over equal intervals
All \(x\)-intervals have length \(1\).
\([-2,-1] : \quad 2 – 5 = -3 \)
\([-1,0]: \quad 1 – 2 = -1 \)
\([0,1]: \quad 2 – 1 = 1\)
So the rates of change are
\(
-3,\,-1,\,1.
\)
Step 2: Identify the pattern
The rates of change are not constant, so \(f\) is not linear.
Now check whether the rates follow a linear rule.
Label each interval by its left endpoint \(x=-2,-1,0\):
\(
2x+1 =
\begin{cases}
2(-2)+1=-3, \\
2(-1)+1=-1, \\
2(0)+1=1.
\end{cases}
\)
This matches the observed rates of change.
Step 3: Conclusion
Since the first differences follow a linear pattern, \(f\) could be a quadratic function.
\(
\boxed{\text{Correct answer: (D)}}
\)
Question
(B) Because \( h \) is negative and constant, the graphs of \( g \) and \( f \), as well as \( h \), are concave down.
(C) Because \( h \) is negative and constant, \( g \) is decreasing, and the graph of \( f \) always has negative slope.
(D) Because \( h \) is negative and constant, \( g \) is decreasing, and the graph \( f \) is concave down.
▶️ Answer/Explanation
We have:
\( g(x) = f(x+1) – f(x) \) → average rate of change of \( f \) over interval \([x, x+1]\).
\( h(x) = g(x+1) – g(x) \) → change in \( g \) from \( x \) to \( x+1 \).
Given \( h(x) = -6 \) for all \( x \).
Thus \( g(x+1) – g(x) = -6 \) ⇒ \( g \) is decreasing linearly with slope \(-6\).
But \( g \) itself is the rate of change of \( f \) (over 1-unit intervals).
Since \( g \) is decreasing, the rate of change of \( f \) is decreasing ⇒ the graph of \( f \) is concave down.
Also, \( g \) decreasing does **not** mean \( g \) is negative, only that it’s getting smaller. So \( f \) could still have positive slope if \( g > 0 \).
Thus: \( h \) constant negative ⇒ \( g \) decreasing ⇒ \( f \) concave down.
✅ Answer: (D)
Question
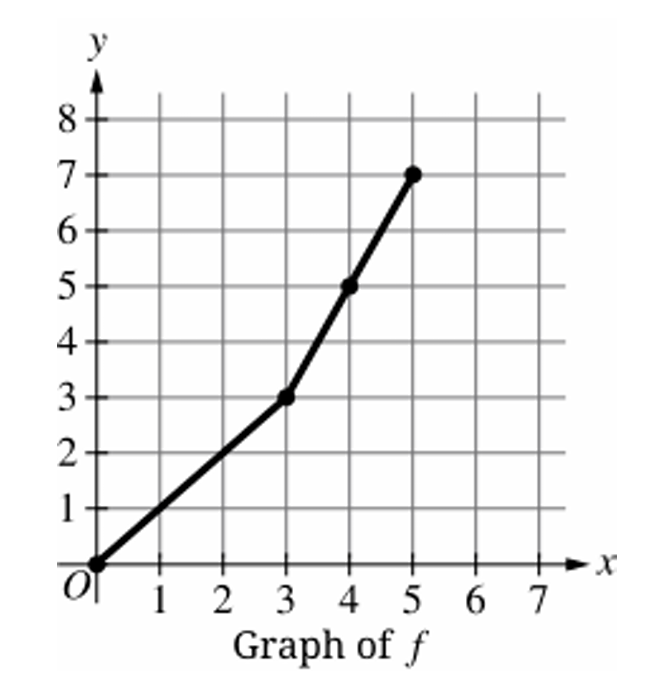
▶️ Answer/Explanation
The function $g$ is defined as the inverse of $f$, meaning $g = f^{-1}$.
By the property of inverse functions, the range of $f$ becomes the domain of $g$.
Similarly, the domain of $f$ becomes the range of $g$.
The maximum value of $g$ is the maximum value in its range, which is the maximum $x$-value of $f$.
Looking at the provided graph, the function $f$ is defined on the interval $x \in [0, 5]$.
The largest $x$-coordinate reached by the graph of $f$ is $5$.
Therefore, the maximum value of the inverse function $g$ is $5$.
The correct option is (C).
Question
▶️ Answer/Explanation
For a quadratic function, the average rate of change over equal-length adjacent intervals forms an arithmetic progression.
The length of the given intervals is constant at $\Delta x = 2$.
The first interval $[0, 2]$ has an average rate of change of $-4$.
The second interval $[2, 4]$ has an average rate of change of $-1$.
The common difference between these rates is $(-1) – (-4) = 3$.
The third interval $[4, 6]$ would have a rate of $(-1) + 3 = 2$.
The fourth interval $[6, 8]$ would have a rate of $2 + 3 = 5$.
Therefore, the average rate of change on $6 \leq x \leq 8$ is $5$.
Question
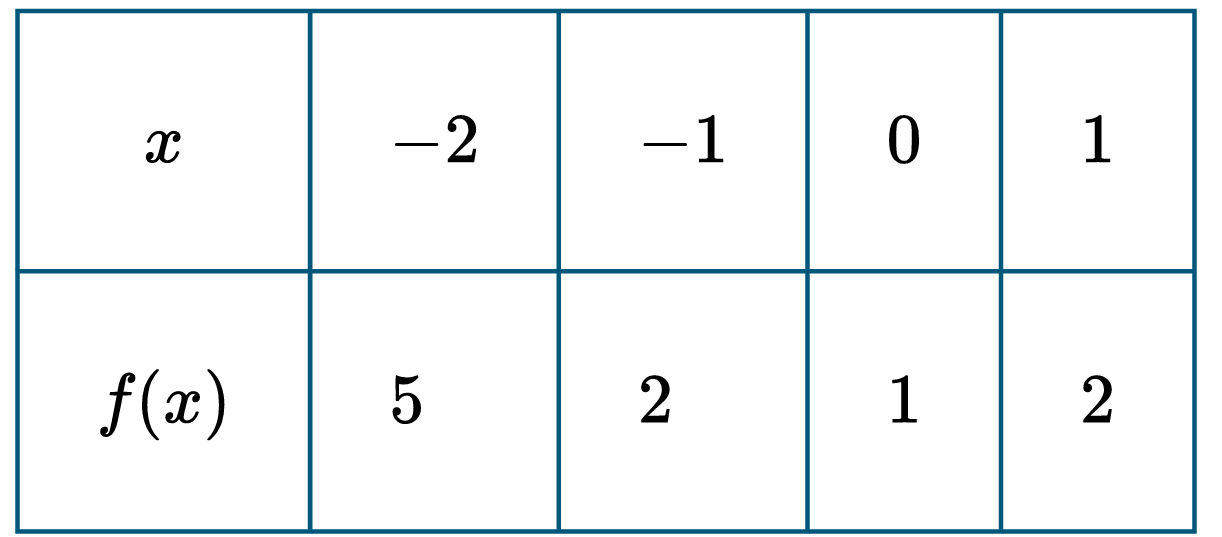
▶️ Answer/Explanation
The correct option is (D).
First, calculate the average rates of change for each interval of width $\Delta x = 1$:
For $[-2, -1]$, the rate is $\frac{2 – 5}{-1 – (-2)} = -3$.
For $[-1, 0]$, the rate is $\frac{1 – 2}{0 – (-1)} = -1$.
For $[0, 1]$, the rate is $\frac{2 – 1}{1 – 0} = 1$.
Since the rates of change are not constant, the function cannot be linear.
The rates of change $\{-3, -1, 1\}$ follow a linear pattern described by $y = 2x + 1$ (where $x$ is the left endpoint).
Because the first differences are linear, the function $f$ could be quadratic.
Question
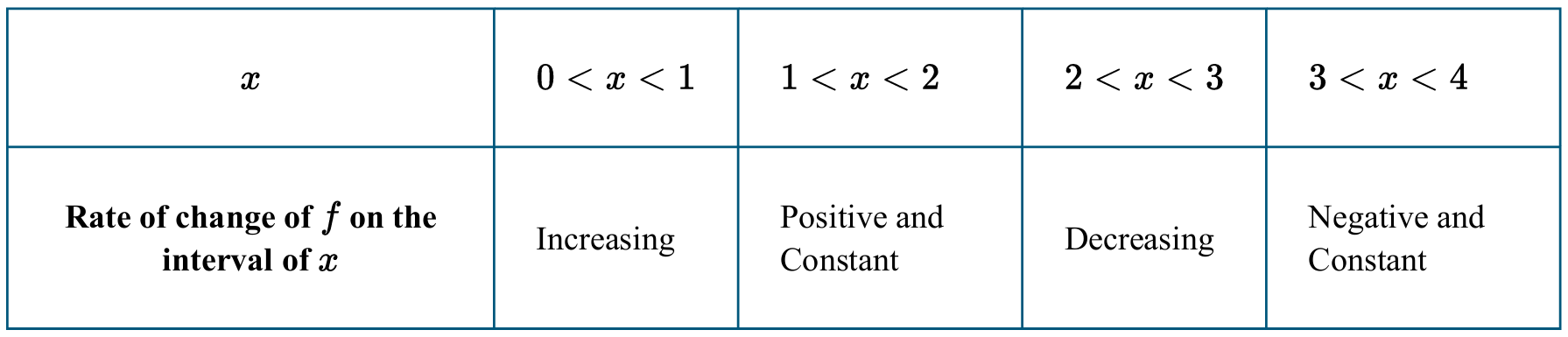
(B) $1 < x < 2$
(C) $2 < x < 3$
(D) $3 < x < 4$
▶️ Answer/Explanation
Concavity is determined by the behavior of the rate of change (the first derivative, $f’$).
A function is concave down on an interval if its rate of change is decreasing.
In the interval $0 < x < 1$, the rate of change is increasing, so the graph is concave up.
In the interval $1 < x < 2$, the rate of change is constant, so the graph is linear.
In the interval $2 < x < 3$, the rate of change is decreasing, which fits the definition of concave down.
In the interval $3 < x < 4$, the rate of change is constant, so the graph is linear.
Therefore, the graph of $f$ is concave down only on the interval $2 < x < 3$.
The correct option is (C).
Question (Calc allowed)
▶️ Answer/Explanation
The initial height at $t = 0$ is $h(0) = 15.24$ meters, but the positive linear term $+4.4t$ indicates the ball is thrown upward first.
The time to reach maximum height is $t = \frac{-b}{2a} = \frac{-4.4}{2(-4.9)} \approx 0.449$ seconds.
The maximum height is $h(0.449) = -4.9(0.449)^2 + 4.4(0.449) + 15.24 \approx 16.228$ meters.
To find when it hits the ground, set $h(t) = 0$ and solve $-4.9t^2 + 4.4t + 15.24 = 0$ using the quadratic formula.
The positive root is $t \approx 2.269$ seconds, which is the total time from the window to the ground.
The time from the maximum height to the ground is $2.269 – 0.449 = 1.820$ seconds.
Therefore, the height increases to $16.228$ m, then decreases for $1.820$ seconds until it hits the ground.
Correct Option: (C)
Question
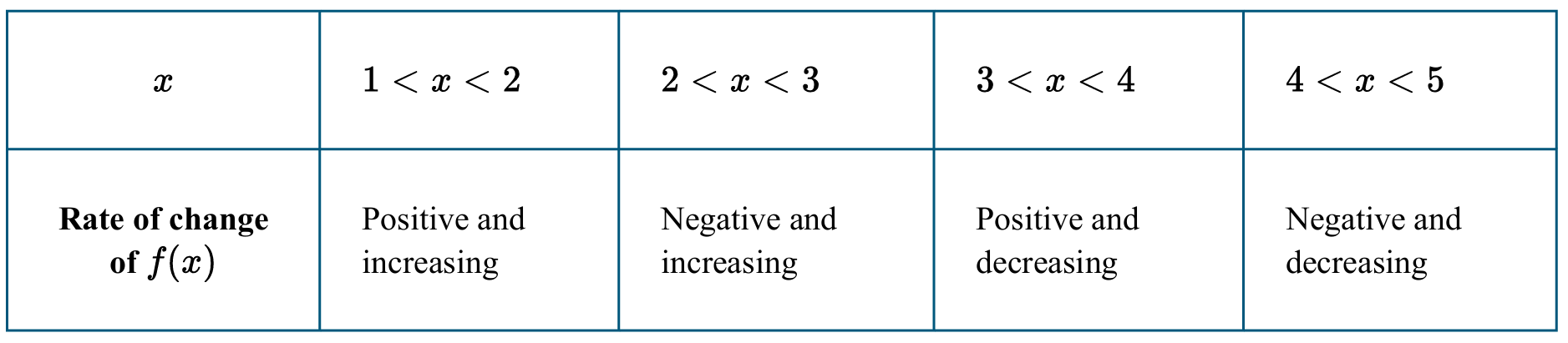
(B) $f$ is increasing, and the graph of $f$ is concave up.
(C) $f$ is decreasing, and the graph of $f$ is concave down.
(D) $f$ is decreasing, and the graph of $f$ is concave up.
▶️ Answer/Explanation
The “rate of change of $f(x)$” corresponds to the first derivative, $f'(x)$.
On the interval $3 < x < 4$, the rate of change is positive, meaning $f'(x) > 0$.
A positive first derivative indicates that the function $f$ is increasing.
The table also specifies that the rate of change is decreasing.
This implies the second derivative, $f”(x)$, is negative because $f'(x)$ is falling.
A negative second derivative ($f”(x) < 0$) means the graph of $f$ is concave down.
Combining these facts, $f$ is increasing and concave down, which is option (A).
Question
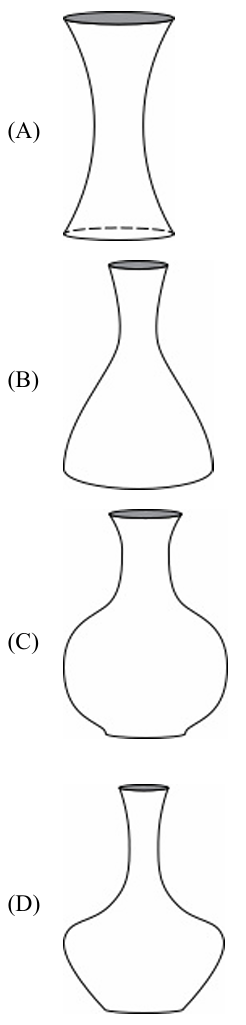
▶️ Answer/Explanation
The rate of change of depth $\frac{dh}{dt}$ is inversely proportional to the cross-sectional area of the vase.
A concave up graph indicates that $\frac{d^2h}{dt^2} > 0$, meaning the vase must be narrowing as height increases.
Vase (D) starts with a wide base that curves inward, causing the water level to rise faster and faster (concave up).
A steady and steep increase implies a constant, high rate of change, which occurs in a narrow, cylindrical neck.
Vase (D) features a long, uniform, and very narrow neck, which produces a linear and steep depth-time relationship.
Vase (B) lacks the uniform vertical neck required for a “steady” increase, as its width continues to change at the top.
Vase (A) and (C) do not match the concave up start because they begin by widening at the bottom.
Therefore, Vase (D) is the correct choice as it perfectly aligns with both geometric descriptions in the graph.
Question

(A) 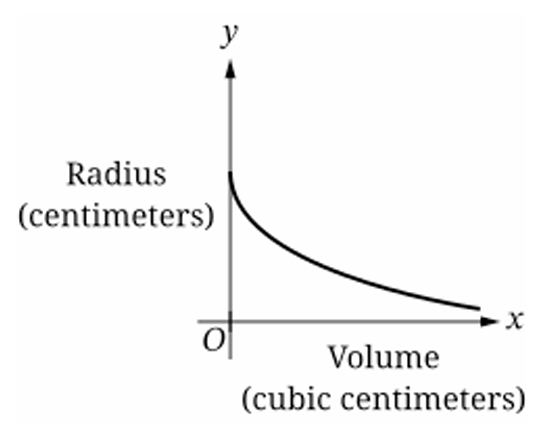
(B) 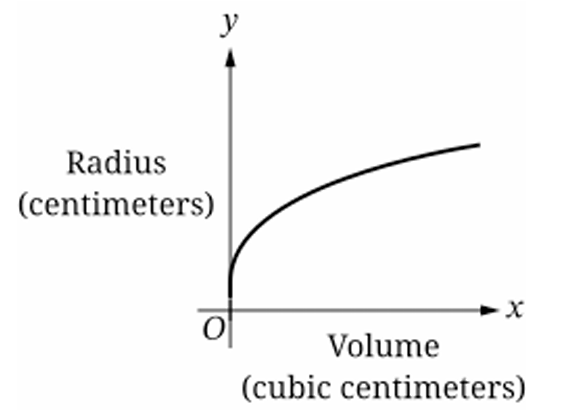
(C) 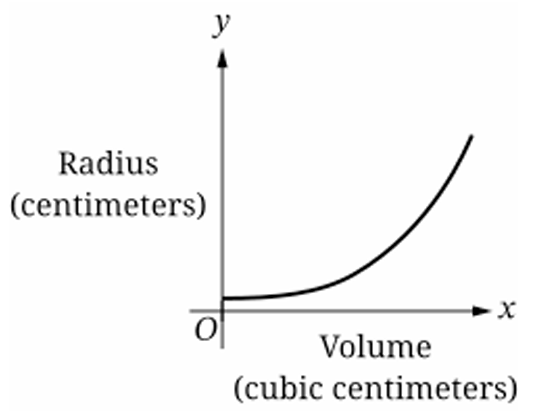
(D) 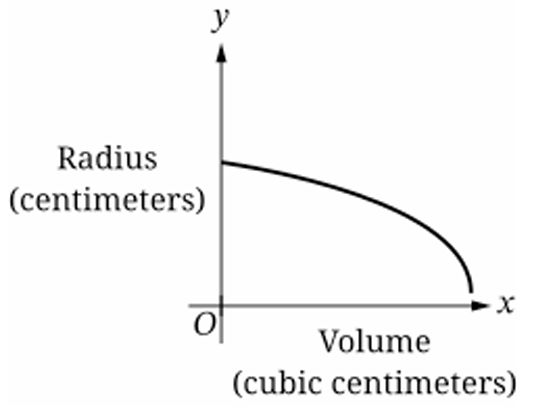
▶️ Answer/Explanation
The volume of a sphere is given by $V = \frac{4}{3}\pi r^{3}$, so the radius is $r = \sqrt[3]{\frac{3V}{4\pi}}$.
Since the radius $r$ increases as volume $V$ increases, the graph must have a positive slope.
The problem states the radius increases at a decreasing rate with respect to volume.
This means the slope $\frac{dr}{dV}$ is positive but getting smaller, indicating a concave down shape.
Graph (A) shows a decreasing radius, which contradicts the expansion of the sphere.
Graph (B) shows an increasing radius with a decreasing rate (concave down), matching the description.
Graph (C) shows an increasing rate (concave up), and Graph (D) shows a decreasing radius.
Therefore, the correct graph depicting this relationship is (B).
Question
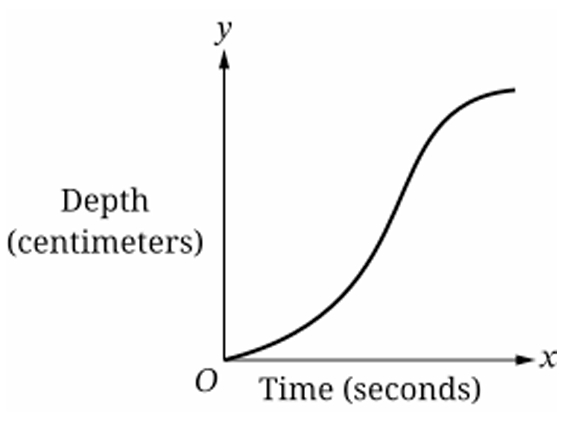
▶️ Answer/Explanation
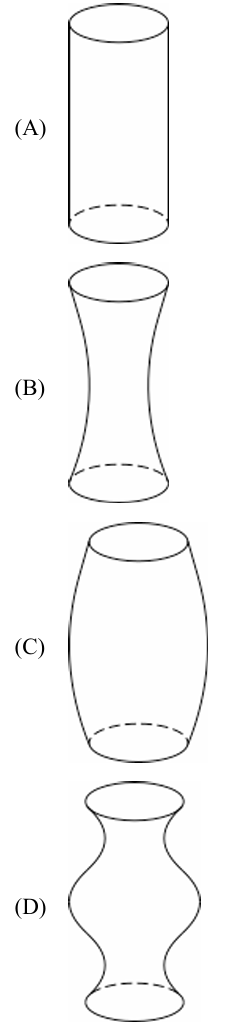
The graph shows an S-shaped (sigmoidal) curve.
Initially, the slope is increasing, meaning the depth rises faster as the container narrows.
This indicates the bottom of the container is wide and gets narrower.
In the middle, the slope is steepest where the container is narrowest.
Then, the slope decreases, meaning the depth rises slower as the container widens again.
This matches a container that is wide at the bottom, narrow in the middle, and wide at the top.
Therefore, the correct container is (B).
Question
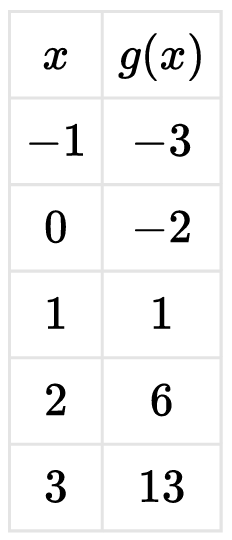
▶️ Answer/Explanation
1. Compute first differences: \( -2 – (-3) = 1 \), \( 1 – (-2) = 3 \), \( 6 – 1 = 5 \), \( 13 – 6 = 7 \).
2. First differences are \( 1, 3, 5, 7 \) (not constant).
3. Compute second differences: \( 3 – 1 = 2 \), \( 5 – 3 = 2 \), \( 7 – 5 = 2 \).
4. Second differences are constant and equal to \( 2 \).
5. A constant second difference indicates a quadratic function.
6. Therefore, the correct statement is that \( g \) is best modeled by a quadratic function.
7. Hence, option (D) is correct.
Question
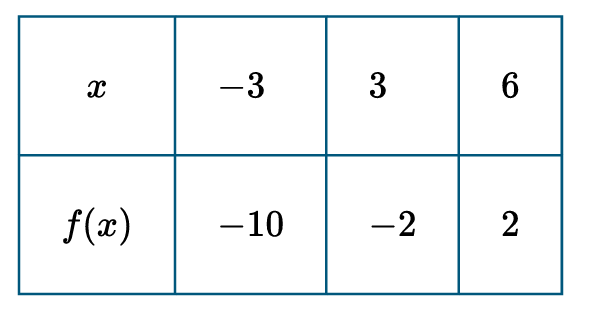
▶️ Answer/Explanation
First, calculate the slope (\( m \)) of the linear function using the points \( (-3, -10) \) and \( (3, -2) \):
\( m = \frac{y_2 – y_1}{x_2 – x_1} = \frac{-2 – (-10)}{3 – (-3)} = \frac{8}{6} = \frac{4}{3} \).
Next, use the point-slope form or slope-intercept form \( y = mx + b \) to find the equation. Using point \( (3, -2) \):
\( -2 = \frac{4}{3}(3) + b \implies -2 = 4 + b \implies b = -6 \).
The function is defined as \( f(x) = \frac{4}{3}x – 6 \).
Substitute \( x = 13 \) into the equation to find the required value:
\( f(13) = \frac{4}{3}(13) – 6 = \frac{52}{3} – \frac{18}{3} = \frac{34}{3} \).
Therefore, the correct value is \( \frac{34}{3} \), which matches option (D).
Question

Two drones are flying over a given area, and their heights above the ground are changing. The table gives the change in height, in feet, for the drones over successive \(6\)-second intervals. Which of the following is true about the average rates of change for drone A and drone B over the time interval from \(t = 0\) seconds to \(t = 30\) seconds?
(A) The average rates of change are equal.
(B) The average rate of change for drone A is greater than for drone B.
(C) The average rate of change for drone B is greater than for drone A.
(D) The average rates of change cannot be determined because changes in heights are given, not heights of the drones.
▶️ Answer/Explanation
The average rate of change is defined as the total change in height divided by the total time elapsed.
First, calculate the total change in height for Drone A by summing the changes in each interval: \(17 + (-4) + 11 + (-5) + (-3) = 16 \text{ feet}\).
Next, calculate the total change in height for Drone B by summing its respective changes: \(5 + 3 + 3 + 2 + 3 = 16 \text{ feet}\).
Both drones experienced the same total change in height (\(16 \text{ ft}\)) over the same total time interval (\(30 \text{ seconds}\)).
Since both the numerator (change in height) and denominator (time) are identical for both drones, their average rates of change are equal (\(\frac{16}{30} \text{ ft/s}\)).
Therefore, the correct statement is that the average rates of change are equal.
Correct Option: (A)
Question
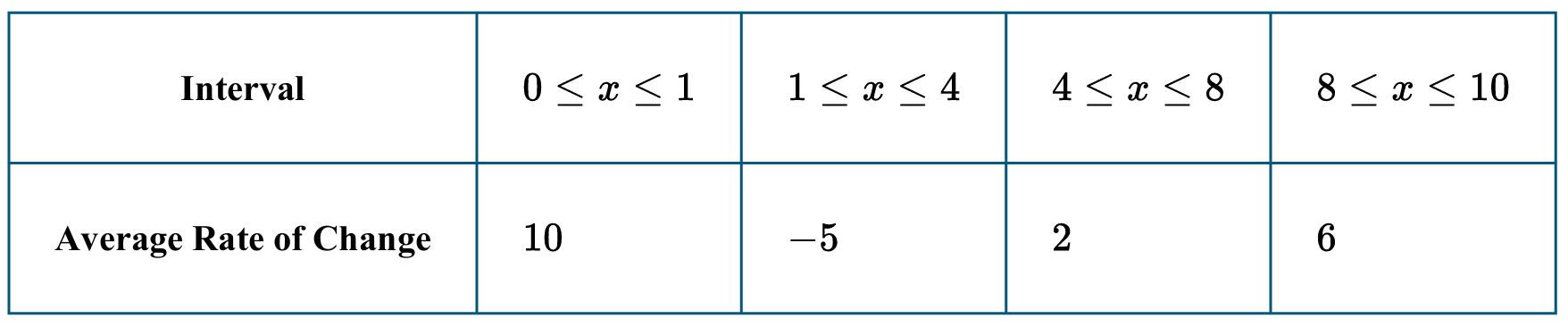
▶️ Answer/Explanation
(C) \( 4 \le x \le 8 \)
The total increase over an interval equals: \[ \text{Average Rate of Change} \times \text{Length of Interval}. \]
Compute each increase:
\(0 \le x \le 1:\; 10 \times (1-0) = 10\)
\(1 \le x \le 4:\; (-5) \times (4-1) = -15\)
\(4 \le x \le 8:\; 2 \times (8-4) = 8\)
\(8 \le x \le 10:\; 6 \times (10-8) = 12\)
The greatest positive increase is \(12\), which occurs on \(8 \le x \le 10\).
1. Increase = (average rate of change) × (interval length).
2. For \(0 \le x \le 1\): \(10 \times 1 = 10\).
3. For \(1 \le x \le 4\): \((-5) \times 3 = -15\).
4. For \(4 \le x \le 8\): \(2 \times 4 = 8\).
5. For \(8 \le x \le 10\): \(6 \times 2 = 12\).
6. Largest increase is \(12\), so the correct interval is \(8 \le x \le 10\).
Question
▶️ Answer/Explanation
The average rate of change from \(x=a\) to \(x=a+1\) is \(2a+1\), which is a linear expression in \(a\). Since \(2a+1\) increases at a constant rate (slope \(2\)), the average rates of change over equal intervals increase linearly. A function whose average rate of change increases linearly is quadratic, meaning its graph is a parabola that opens upward. Therefore, statement (D) is correct.
1. The average rate of change on \([a,a+1]\) is \(2a+1\).
2. This expression is linear in \(a\) with constant slope \(2\).
3. Therefore, consecutive average rates increase at a constant rate.
4. A constant first difference implies a quadratic function.
5. The leading coefficient is positive since the rate increases.
6. Hence, the graph is a parabola opening upward.
7. Therefore, the correct statement is (D).
Question
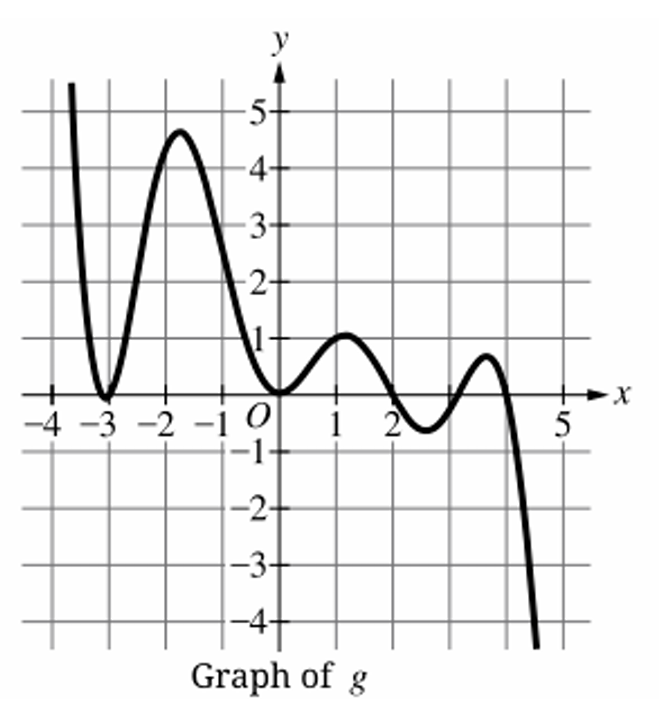
▶️ Answer/Explanation
(D) \( 3 \le x \le 4 \)
The average rate of change on an interval \( [a,b] \) is \[ \frac{g(b)-g(a)}{b-a}. \] We estimate values from the graph and compute slopes. The least average rate of change corresponds to the most negative slope.
1. For \( -3 \le x \le -2 \): \( \frac{g(-2)-g(-3)}{1} \approx \frac{4.5-0}{1} = 4.5 \).
2. For \( -1 \le x \le 0 \): \( \frac{g(0)-g(-1)}{1} \approx \frac{0-4}{1} = -4 \).
3. For \( 1 \le x \le 2 \): \( \frac{g(2)-g(1)}{1} \approx \frac{-1-1}{1} = -2 \).
4. For \( 3 \le x \le 4 \): \( \frac{g(4)-g(3)}{1} \approx \frac{-4-0.5}{1} = -4.5 \).
5. The smallest (most negative) value is \( -4.5 \).
6. Therefore, the least average rate of change occurs on \( 3 \le x \le 4 \).
Question (Calc Allowed)
▶️ Answer/Explanation
Explanation:
The rate of change of a function is given by its derivative. \( f(x) = x^2 + 3x – 5 \) is a quadratic function that opens upward since the coefficient of \( x^2 \) is positive. Its derivative is \( f'(x) = 2x + 3 \). Setting \( f'(x) = 0 \) gives \( 2x + 3 = 0 \Rightarrow x = -\dfrac{3}{2} = -1.5 \). For \( x < -1.5 \), \( f'(x) < 0 \), so the function is decreasing. For \( x > -1.5 \), \( f'(x) > 0 \), so the function is increasing. Therefore, option (D) correctly describes the function.
1. Given \( f(x) = x^2 + 3x – 5 \).
2. Compute derivative: \( f'(x) = 2x + 3 \).
3. Set derivative equal to zero: \( 2x + 3 = 0 \).
4. Solve: \( x = -\dfrac{3}{2} = -1.5 \).
5. If \( x < -1.5 \), then \( f'(x) < 0 \) → decreasing.
6. If \( x > -1.5 \), then \( f'(x) > 0 \) → increasing.
7. Hence, the correct answer is (D).
Question
▶️ Answer/Explanation
Since \(p(x)\) is quadratic, its average rate of change over equal-length intervals changes linearly. The intervals \(0 \le x \le 2\), \(2 \le x \le 4\), \(4 \le x \le 6\), and \(6 \le x \le 8\) each have length \(2\). The given average rates are \(-4\) and \(-1\), increasing by \(3\). Therefore, the sequence continues increasing by \(3\): \(2\), then \(5\). Hence, the average rate of change on \(6 \le x \le 8\) is \(5\).
1. For a quadratic function, average rates over equal intervals form an arithmetic sequence.
2. Interval length is \(2\) for all given intervals.
3. Given rates: \(-4\) and \(-1\).
4. Common difference \(= -1 – (-4) = 3\).
5. Next interval \(4 \le x \le 6\): \( -1 + 3 = 2\).
6. Next interval \(6 \le x \le 8\): \( 2 + 3 = 5\).
7. Therefore, required average rate of change \(= 5\).
Question
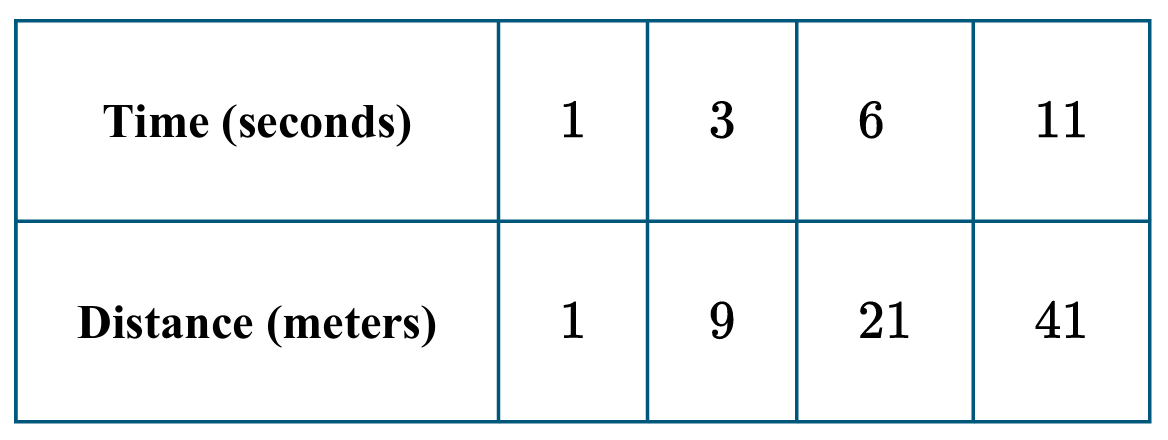
▶️ Answer/Explanation
1. Calculate the rate of change of distance (velocity) for the intervals: \( \frac{9-1}{3-1} = 4 \), \( \frac{21-9}{6-3} = 4 \), and \( \frac{41-21}{11-6} = 4 \).
2. The velocity is constant at \( 4 \, \text{m/s} \) for all time intervals shown.
3. The “rate of change of the rates of change” is the acceleration (derivative of velocity).
4. Since the velocity is constant, the change in velocity is zero, so acceleration is \( 0 \, \text{m/s}^2 \).
5. The correct unit for acceleration is meters per second per second (\( \text{m/s}^2 \)).
6. Since acceleration is \( 0 \), the object is moving at a steady speed, neither speeding up nor slowing down.
7. Therefore, option (B) matches both the value and the description of the motion.
Question
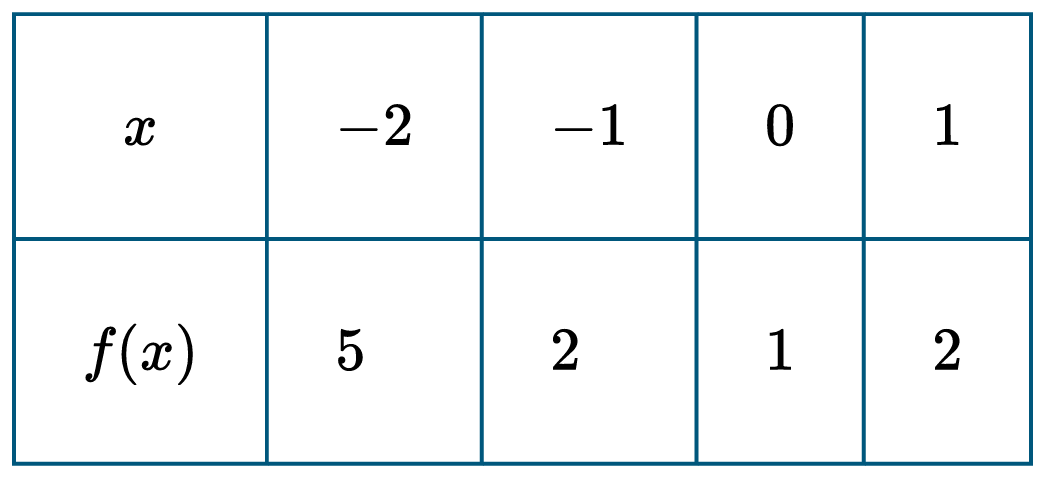
▶️ Answer/Explanation
The correct answer is (D).
First, calculate the first differences (rates of change) between consecutive \( f(x) \) values:
\( f(-1) – f(-2) = 2 – 5 = -3 \)
\( f(0) – f(-1) = 1 – 2 = -1 \)
\( f(1) – f(0) = 2 – 1 = 1 \)
Since the first differences (\(-3, -1, 1\)) are not constant, \( f \) is not linear.
Next, calculate the second differences: \( -1 – (-3) = 2 \) and \( 1 – (-1) = 2 \). Since the second differences are constant, \( f \) could be a quadratic function.
Finally, check which linear equation describes the rates of change (\(-3, -1, 1\)) based on the starting \( x \) values (\(-2, -1, 0\)):
Using \( y = 2x + 1 \): for \( x = -2 \), \( y = -3 \); for \( x = -1 \), \( y = -1 \); for \( x = 0 \), \( y = 1 \).
This matches the calculated rates perfectly.
Question
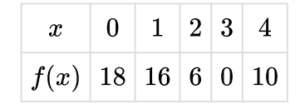
▶️ Answer/Explanation
Question
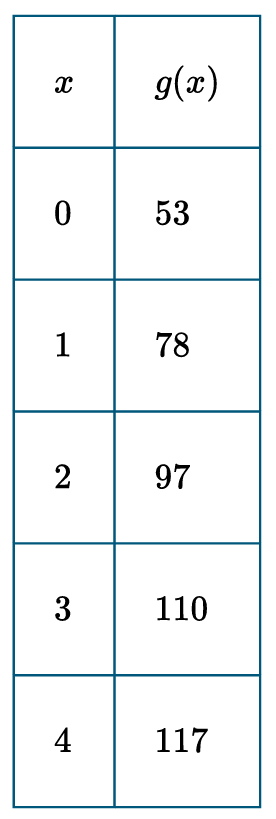
▶️ Answer/Explanation
Explanation:
The first differences (average rates of change) are:
\( 78-53 = 25 \),
\( 97-78 = 19 \),
\( 110-97 = 13 \),
\( 117-110 = 7 \).
These are not constant, so the function is not linear.
The second differences are:
\( 19-25 = -6 \),
\( 13-19 = -6 \),
\( 7-13 = -6 \).
Since the second differences are constant (\(-6\)), the function is quadratic.
2. These values are not constant ⇒ not linear.
3. Compute second differences: \(19-25=-6\).
4. \(13-19=-6\).
5. \(7-13=-6\).
6. Second differences are constant ⇒ quadratic model.
7. Therefore, option (D) is correct.
Question

▶️ Answer/Explanation
1. Since \( a < b \Rightarrow g(a) > g(b) \), the function is decreasing on \( 3 < x < 7 \).
2. Compute average rates of change over intervals of length \( 1 \):
3. \( \frac{-19 – (-11)}{4-3} = -8 \), \( \frac{-29 – (-19)}{5-4} = -10 \).
4. \( \frac{-41 – (-29)}{6-5} = -12 \), \( \frac{-55 – (-41)}{7-6} = -14 \).
5. The average rates of change are \( -8, -10, -12, -14 \), which are decreasing (becoming more negative).
6. A decreasing function with decreasing slopes indicates the graph is concave down.
7. Therefore, the correct statement is (C).
Question
Part A
Part B
Part C
▶️ Answer/Explanation
Part A
(i)
Using the data $M(6) = 508.67$ and $M(12) = 517.50$:
$ab^{(6/12)} = 508.67$ (or $ab^{0.5} = 508.67$)
$ab^{(12/12)} = 517.50$ (or $ab = 517.50$)
(ii)
Divide the second equation by the first: $\frac{ab}{ab^{0.5}} = \frac{517.50}{508.67}$
$b^{0.5} \approx 1.017359…$
$b \approx (1.017359…)^2 \approx 1.035019…$
Using $ab = 517.50 \implies a = \frac{517.50}{1.035019…} \approx 500$
Final values: $a \approx 500.00$ and $b \approx 1.035$
Part B
(i)
$t = -2$ falls in the interval $-10 \le t < 0$, so $M(-2) = 500$.
$t = 12$ is given as $M(12) = 517.50$.
Average Rate of Change $= \frac{M(12) – M(-2)}{12 – (-2)}$
$= \frac{517.50 – 500}{12 + 2}$
$= \frac{17.50}{14} = 1.25$ dollars per month.
(ii)
The linear estimate $A(t)$ uses the point $(12, 517.50)$ and slope $1.25$.
$A(20) = M(12) + 1.25(20 – 12)$
$A(20) = 517.50 + 1.25(8)$
$A(20) = 517.50 + 10 = 527.50$ dollars.
(iii)
The model $M(t)$ for $t \ge 0$ is an exponential function ($b > 1$), which is concave up.
The estimate $A(t)$ is a linear function (a secant line).
Since $M(t)$ is increasing at an increasing rate (exponential growth), the linear model will fall further behind the actual values as $t$ increases.
Part C
The model is only valid as long as the account is open.
Setting $M(t) = 565$ allows us to solve for the maximum value of $t$.
$500(1.035)^{(t/12)} = 565$
This value of $t$ serves as the upper bound (maximum) for the domain of the model $M$.
Question
▶️ Answer/Explanation
a. Graphing the function
Using a graphing utility for \(P(x) = -0.0013x^3 + 0.3507x^2 – 0.4591x – 421.888\) on the interval \([0, 200]\) reveals a cubic curve shape.
The graph starts with a slight dip to a local minimum near \(x=0\), then rises steeply to a local maximum near \(x=180\), before falling again.
b. Average rate of change between extrema
First, find the derivative: \(P'(x) = -0.0039x^2 + 0.7014x – 0.4591\).
Set \(P'(x) = 0\) and use the quadratic formula to find the extrema: \(x \approx 0.66\) (local min) and \(x \approx 179.19\) (local max).
Calculate the profit at these points: \(P(0.66) \approx -422.04\) and \(P(179.19) \approx 3276.57\).
The average rate of change is: \(\frac{3276.57 – (-422.04)}{179.19 – 0.66} = \frac{3698.61}{178.53} \approx 20.72\).
c. Equation of the secant line
The slope \(m\) was found in part (b) to be approximately \(20.72\).
Using the point-slope form \(y – y_1 = m(x – x_1)\) with the minimum point \((0.66, -422.04)\):
\(y – (-422.04) = 20.72(x – 0.66)\)
\(y = 20.72x – 13.68 – 422.04\)
The equation is approximately \(y = 20.72x – 435.72\).
d. Inflection point
Find the second derivative: \(P”(x) = -0.0078x + 0.7014\).
Set \(P”(x) = 0\) to find the change in concavity: \(0 = -0.0078x + 0.7014 \Rightarrow x = \frac{0.7014}{0.0078} \approx 89.92\).
Find the corresponding y-value: \(P(89.92) \approx 1427.27\).
The inflection point is approximately \((89.92, 1427.27)\).
e. Variation of rate of change
The rate of change is represented by the derivative, \(P'(x)\).
Before the inflection point (\(x < 89.92\)), the graph is concave up (\(P”(x) > 0\)), so the rate of change is increasing.
After the inflection point (\(x > 89.92\)), the graph is concave down (\(P”(x) < 0\)), so the rate of change is decreasing.
Question
▶️ Answer/Explanation
(A)(i) Equations
Substituting the points \((1, 3)\) and \((5, 89)\) into \(H(t) = ab^t\):
1. \(3 = ab^1\) (or \(3 = ab\))
2. \(89 = ab^5\)
(A)(ii) Values for a and b
Dividing equation 2 by equation 1: \(\frac{ab^5}{ab} = \frac{89}{3} \implies b^4 = 29.67\).
Solving for \(b\): \(b = (29.67)^{0.25} \approx 2.33\).
Solving for \(a\): \(a = \frac{3}{2.33} \approx 1.29\).
(B)(i) Average Rate of Change
\(\text{Rate} = \frac{H(5) – H(1)}{5 – 1} = \frac{89 – 3}{4} = \frac{86}{4} = 21.5\)
Answer: 21.5 feet per week.
(B)(ii) Interpretation
The answer indicates that between the first and fifth weeks, the bamboo tree grew at an average speed of 21.5 feet per week.
(B)(iii) Comparison
Greater. The function represents exponential growth (\(b > 1\)), which is concave up. This means the rate of growth increases over time, so the rate after week 5 will be steeper than the rate before week 5.
(C) Confidence
\(t = 4\) weeks.
The biologists should be more confident in \(t=4\) because it is an interpolation (within the observed data range). \(t=11\) is an extrapolation; biological growth cannot remain exponential indefinitely, so the model is likely inaccurate that far out.