AP Precalculus -1.4 Polynomial Functions and Rates of Change- MCQ Exam Style Questions - Effective Fall 2023
AP Precalculus -1.4 Polynomial Functions and Rates of Change- MCQ Exam Style Questions – Effective Fall 2023
AP Precalculus -1.4 Polynomial Functions and Rates of Change- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.
Question
▶️ Answer/Explanation
From the given answer and typical AP graph problems: Graph has zeros at \( x = 5 \) (touch/bounce, so multiplicity even), \( x = 1 \) (cross), \( x = -8 \) (cross). Degree is even (since both ends go in the same direction) and positive leading coefficient (both ends up).
Thus factors: \( (x – 5)^2 \) for the even-multiplicity zero, \( (x – 1) \) and \( (x + 8) \) for the simple zeros. Leading coefficient positive and scaled appropriately → matches \( 0.25(x – 5)^2(x – 1)(x + 8) \).
✅ Answer: (C)
Question
(B) \( p(-3) = -4 \) is a relative maximum.
(C) \( p(-3) = 4 \) is a relative minimum.
(D) \( p(-3) = -4 \) is a relative minimum.
▶️ Answer/Explanation
Odd function: \( p(-x) = -p(x) \).
Given \( p(3) = -4 \) ⇒ \( p(-3) = -p(3) = 4 \).
Symmetry of odd functions: if \( (3, -4) \) is a relative maximum, then \( (-3, 4) \) is a relative minimum (since the graph rotated 180° about origin swaps maxima/minima).
✅ Answer: (C)
Question
| \( x \) | -1 | 1 | 3 | 5 | 7 |
|---|---|---|---|---|---|
| \( f(x) \) | -36 | 0 | 4 | 0 | 12 |
(B) The function \( f \) has a local minimum at \( (5, 0) \).
(C) The function \( f \) has a local maximum at \( (3, 4) \).
(D) The function \( f \) has a local maximum at \( (1, 0) \).
▶️ Answer/Explanation
Zeros from table: \( x = 1 \) and \( x = 5 \).
Between \( x = 1 \) and \( x = 5 \), \( f(3) = 4 \) > 0 ⇒ curve is above axis, so zeros at ends with positive in between ⇒ at \( x = 5 \) function goes from positive (at \( x = 3 \)) to 0 (at \( x = 5 \)) then to positive (at \( x = 7 \)), but wait: check \( f(5) = 0 \) and \( f(7) = 12 \) ⇒ from 0 to 12 means increasing through \( x = 5 \). That suggests \( x = 5 \) is a local minimum (touching zero and going up). Similarly \( x = 1 \) is zero but \( f(-1) = -36\), \( f(1) = 0\), \( f(3) = 4 \) ⇒ increasing through \( x = 1 \) ⇒ local minimum? Not necessarily because it could be crossing.
Given answer key says B: local minimum at \( (5, 0) \) is consistent because graph goes up on both sides (from 4 to 0 to 12 is not possible as written unless 4 is at x=3 and 0 at x=5 then 12 at x=7, which means 3 to 5 decreases, 5 to 7 increases ⇒ local min at 5). Actually, check sequence: (3,4), (5,0), (7,12) → decreases then increases ⇒ min at (5,0).
✅ Answer: (B)
Question
▶️ Answer/Explanation
Points of inflection occur where concavity changes (i.e., \( f” \) changes sign).
From typical AP problems, the given graph likely shows a polynomial with three changes in concavity within the visible domain.
✅ Answer: (B)
Question
▶️ Answer/Explanation
From answer explanation: \( f \) has interior local extrema at \( x = 1 \) and \( x = 2.4 \) (approx), plus the endpoints \( x = 0 \) and \( x = 3 \) can be local extrema on a closed interval.
That’s 4 total (two local mins/maxs inside, two at endpoints).
✅ Answer: (B)
Question
| \( x \) | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|---|---|
| \( Q(x) \) | 389 | 139 | 35 | 5 | 1 | -1 | -1 | 25 | 125 |
(B) 3
(C) 4
(D) 5
▶️ Answer/Explanation
For a polynomial of degree \( n \), the \( n \)-th differences are constant and nonzero.
From the answer explanation: fourth differences are constant 24 ⇒ degree = 4.
✅ Answer: (C)
Question
▶️ Answer/Explanation
From answer explanation: zero at \( x = 4 \) has even multiplicity (graph tangent to x-axis), zero at \( x = -3 \) has odd multiplicity (graph crosses x-axis).
Thus: factor \( (x – 4)^2 \) (even), factor \( (x + 3) \) (odd).
Positive leading coefficient ⇒ \( P(x) = \frac{(x-4)^2(x+3)}{12} \).
✅ Answer: (B)
Question
(B) The graph of \( g \) has a maximum at \( x = 2 \).
(C) The graph of \( g \) has a point of inflection at \( x = 2 \), is concave down for \( x < 2 \), and is concave up for \( x > 2 \).
(D) The graph of \( g \) has a point of inflection at \( x = 2 \), is concave up for \( x < 2 \), and is concave down for \( x > 2 \).
▶️ Answer/Explanation
The “rate of change of \( g \)” means \( g'(x) \).
Given \( g'(x) \) is increasing for \( x<2 \) and decreasing for \( x>2 \).
Thus \( x=2 \) is a maximum of \( g'(x) \).
Since \( g'(x) \) changes from increasing to decreasing at \( x=2 \), \( g”(x) = 0 \) at \( x=2 \) and changes sign from positive to negative ⇒ point of inflection for \( g \).
Concavity: \( g” > 0 \) ⇒ concave up (rate of change increasing).
So for \( x<2 \): \( g”>0 \) ⇒ concave up.
For \( x>2 \): \( g”<0 \) ⇒ concave down.
Thus \( g \) has point of inflection at \( x=2 \), concave up for \( x<2 \), concave down for \( x>2 \).
✅ Answer: (D)
Question
| \(x\) | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|
| \(g(x)\) | -11 | -19 | -29 | -41 | -55 |
(B) The graph of \(g\) is concave up because the function is decreasing, and the average rate of change over equal-length input-value intervals is increasing.
(C) The graph of \(g\) is concave down because the function is decreasing, and the average rate of change over equal-length input-value intervals is decreasing.
(D) The graph of \(g\) is concave up because the function is decreasing, and the average rate of change over equal-length input-value intervals is decreasing.
▶️ Answer/Explanation
1. Analyze Decreasing Behavior:
The problem states that if \(a < b\), then \(g(a) > g(b)\). This confirms \(g\) is decreasing on the interval.
2. Calculate Average Rates of Change (Slopes):
Interval [3, 4]: \(\frac{-19 – (-11)}{4-3} = -8\)
Interval [4, 5]: \(\frac{-29 – (-19)}{5-4} = -10\)
Interval [5, 6]: \(\frac{-41 – (-29)}{6-5} = -12\)
Interval [6, 7]: \(\frac{-55 – (-41)}{7-6} = -14\)
3. Determine Concavity:
The rates of change are \(-8, -10, -12, -14\). Since the rate of change is becoming more negative (decreasing), the graph is concave down.
✅ Answer: (C)
Question
(B) \(t=0.451\), because the rate of change in the number of people inside the shopping center changes from positive to negative.
(C) \(t=1.445\) because the rate of change in the number of people inside the shopping center changes from increasing to decreasing.
(D) \(t=1.445\) because the rate of change in the number of people inside the shopping center changes from positive to negative.
▶️ Answer/Explanation
1. Identify the condition for a maximum:
The function \(P(t)\) represents the rate of change of the number of people.
The total number of people is maximized when the rate \(P(t)\) transitions from positive (people entering) to negative (people leaving).
2. Find the zeros of \(P(t)\):
We solve \(P(t) = t^{3}-4t^{2}+3t+1 = 0\) using a graphing calculator on the interval \(0 \le t \le 2\).
The zero occurs at \(t \approx 1.445\).
3. Analyze the sign change:
For \(t < 1.445\), \(P(t) > 0\).
For \(t > 1.445\), \(P(t) < 0\).
Since the rate changes from positive to negative, the number of people is at a maximum.
✅ Answer: (D)
Question
(B) \( t = 17.056 \)
(C) \( t = 13.295 \)
(D) \( t = 5.505 \)
▶️ Answer/Explanation
“Changes from increasing to decreasing” means a local maximum of \( R(t) \), so \( R'(t) = 0 \) and \( R”(t) < 0 \).
\[ R'(t) = 0.09t^2 – 1.692t + 6.587 \]
Set \( R'(t) = 0 \):
\[ 0.09t^2 – 1.692t + 6.587 = 0 \]
Multiply by 100: \( 9t^2 – 169.2t + 658.7 = 0 \).
Solve quadratic: discriminant \( D = (169.2)^2 – 4\cdot 9 \cdot 658.7 \approx 28628.64 – 23713.2 = 4915.44 \).
\[ t = \frac{169.2 \pm \sqrt{4915.44}}{18} \]
\[ \sqrt{4915.44} \approx 70.11 \]
\( t_1 \approx \frac{169.2 – 70.11}{18} \approx \frac{99.09}{18} \approx 5.505 \)
\( t_2 \approx \frac{169.2 + 70.11}{18} \approx \frac{239.31}{18} \approx 13.295 \)
Check second derivative: \( R”(t) = 0.18t – 1.692 \).
At \( t \approx 5.505 \), \( R” \approx 0.18(5.505) – 1.692 \approx 0.9909 – 1.692 < 0 \) ⇒ local max (increasing to decreasing).
At \( t \approx 13.295 \), \( R” > 0 \) ⇒ local min (decreasing to increasing).
So the change from increasing to decreasing occurs at \( t \approx 5.505 \).
✅ Answer: (D)
Question
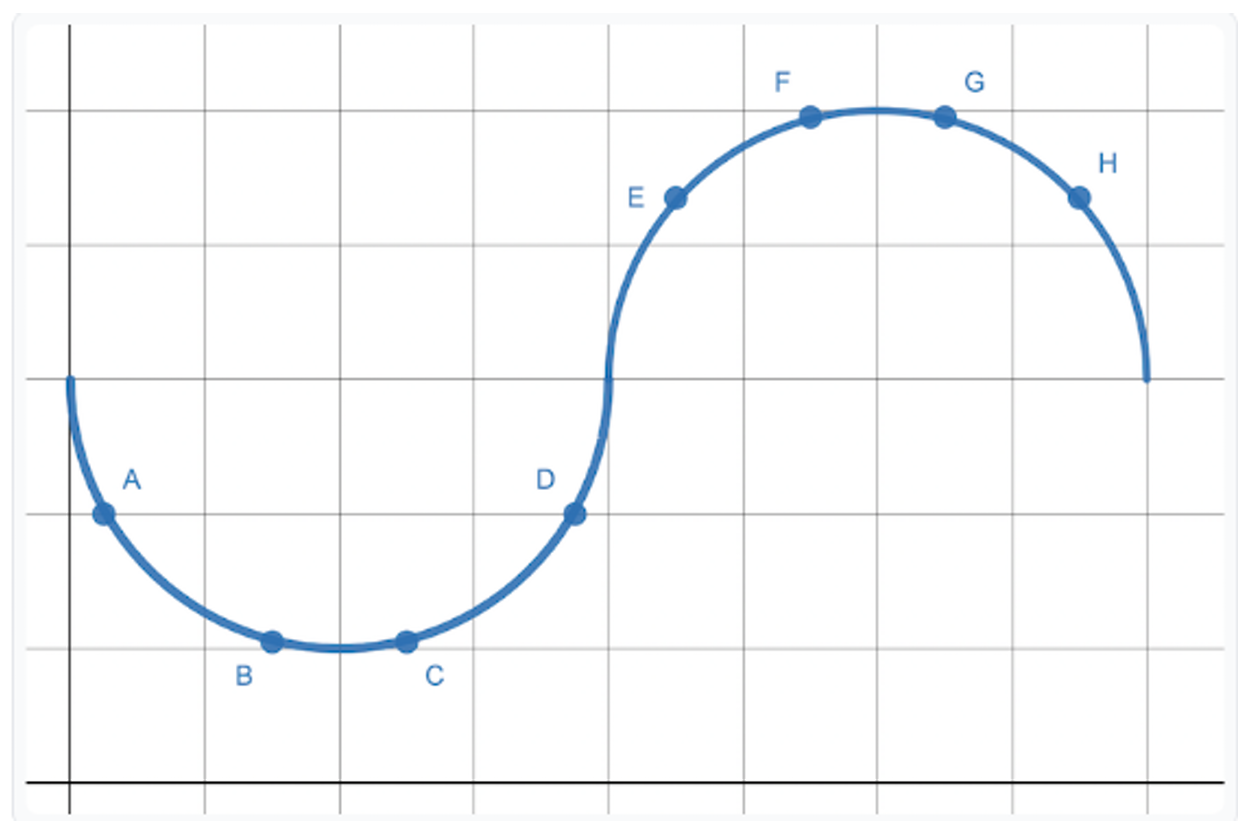
▶️ Answer/Explanation
A point of inflection is a point on a curve at which the concavity changes (from concave up to concave down, or vice versa). This occurs where the second derivative $g”(x)$ changes sign.
- In interval $[B, C]$: The graph is strictly concave down (the “frown” shape), meaning $g”(x) < 0$. No change occurs.
- In interval $[D, E]$: The graph is strictly concave up (the “cup” shape), meaning $g”(x) > 0$. No change occurs.
- In interval $[G, H]$: The curve transitions from being concave up (after the local minimum at F) to concave down (as it approaches the peak after H). Because the “bend” of the graph reverses direction within this window, a point of inflection must exist here.
Question
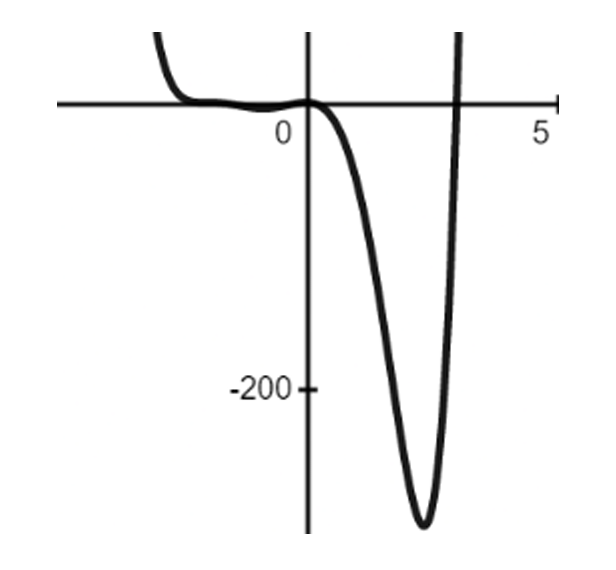
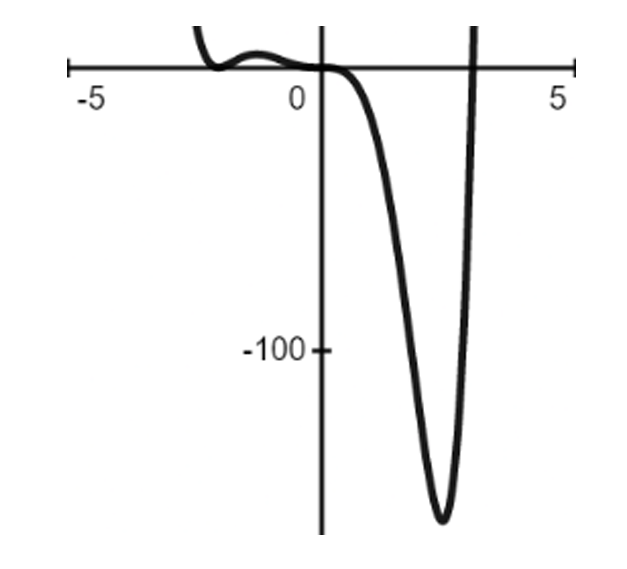
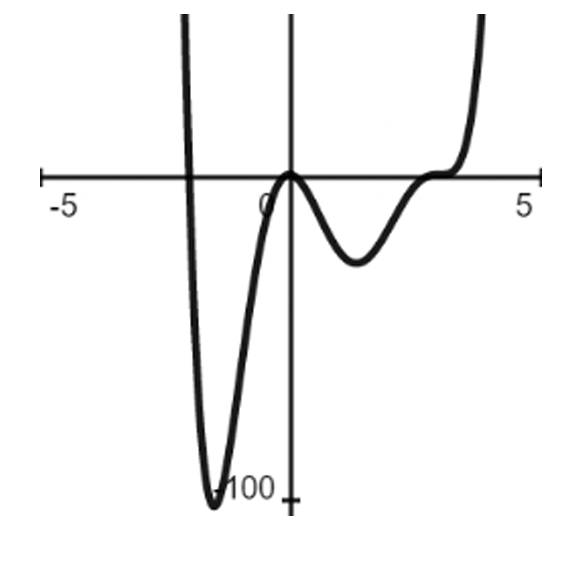
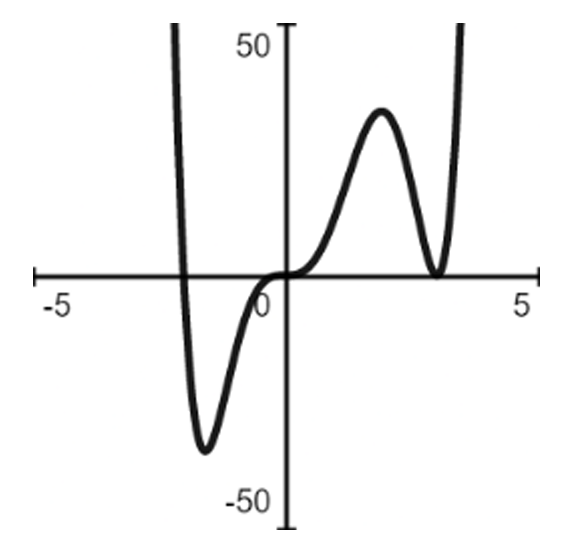
▶️ Answer/Explanation
The correct answer is c.
Identify roots: $x = -2$ (multiplicity $3$), $x = 0$ (multiplicity $2$), and $x = 3$ (multiplicity $1$).
Determine degree: The total degree is $2 + 3 + 1 = 6$, which is an even number.
Leading coefficient: Since it is positive ($+1$), the end behavior is $y \to \infty$ as $x \to \pm\infty$.
At $x = -2$, the graph crosses the x-axis with an “S-curve” (inflection) due to the cubic power.
At $x = 0$, the graph touches and bounces off the x-axis because the power is even ($2$).
At $x = 3$, the graph crosses the axis linearly because the power is odd ($1$).
Graph c is the only one showing the correct bounce at $x = 0$ and the correct end behavior.
Question
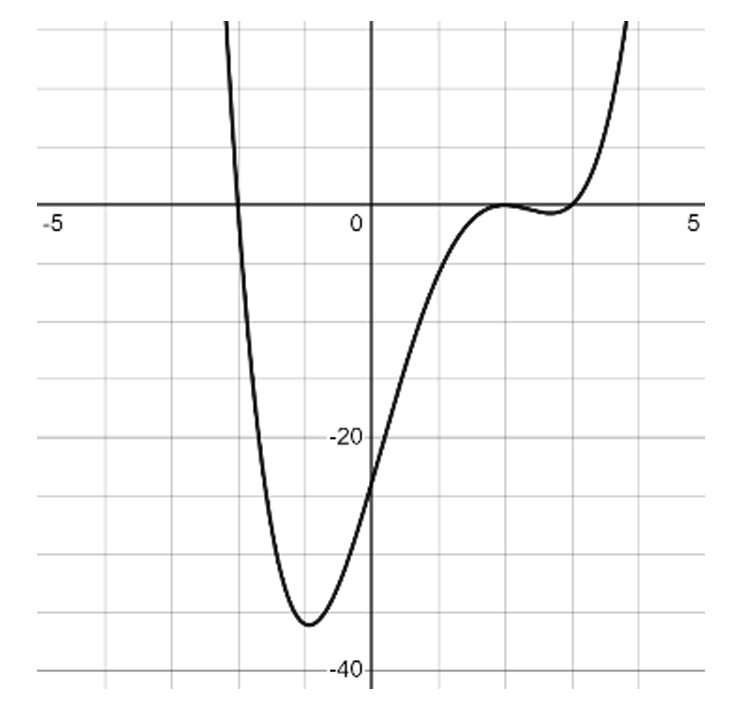
$g(x)$ is continuous on all real numbers with selected $x$ values below:
![]()
b. $g(x)$
c. $h(x)$
d. Both $g(x)$ and $h(x)$
▶️ Answer/Explanation
For $f(x)$, the highest power of $x$ is $5$, so the degree is $5$.
For $g(x)$, the values change sign/direction $3$ times (roots exist between $-18$ and $-12$, $-12$ and $-6$, $-6$ and $0$), implying at least degree $4$.
For $h(x)$, the graph shows $3$ turning points and $2$ x-intercepts (one being a touch/bounce point).
A bounce at an x-intercept indicates a multiplicity of at least $2$, and another crossing indicates at least $1$.
The $3$ turning points on $h(x)$ suggest a minimum degree of $4$.
Both $g(x)$ and $h(x)$ have a minimum degree of $4$, which is lower than $f(x)$’s degree of $5$.
Therefore, both $g(x)$ and $h(x)$ share the lowest potential degree among the choices.
Correct Option: d
Question
▶️ Answer/Explanation
For power functions of the form $x^n$ where $0 < x < 1$, the function with the smallest exponent yields the highest output.
Comparing the given exponents: $9/2 = 4.5$, $4$, $2/3 \approx 0.67$, and $1/7 \approx 0.14$.
The smallest exponent among the choices is $1/7$.
Therefore, $h(x) = x^{1/7}$ will stay closer to $1$ for longer within the interval $(0, 1)$.
For example, if $x = 0.1$, then $0.1^{4.5} < 0.1^4 < 0.1^{2/3} < 0.1^{1/7}$.
Thus, $h(x)$ has the highest output value in the specified range.
The correct option is d.
Question
▶️ Answer/Explanation
First, fully factor the polynomial: \( p(x) = x(x+3)(x-3)(x+3) = x(x-3)(x+3)^2 \).
Identify the zeros (critical points) of the function: \( x = 0 \), \( x = 3 \), and \( x = -3 \).
Analyze the factor \( (x+3)^2 \): it is always positive for all real \( x \neq -3 \), so it does not change the sign of \( p(x) \).
The sign of \( p(x) \) therefore depends on the remaining term \( x(x-3) \).
We solve \( x(x-3) < 0 \), which occurs between the roots, so \( 0 < x < 3 \).
Checking the interval \( (0, 3) \), the condition holds true, and it does not include \( x = -3 \).
Therefore, the interval where \( p(x) < 0 \) is \( (0, 3) \).
Correct Option: (D)
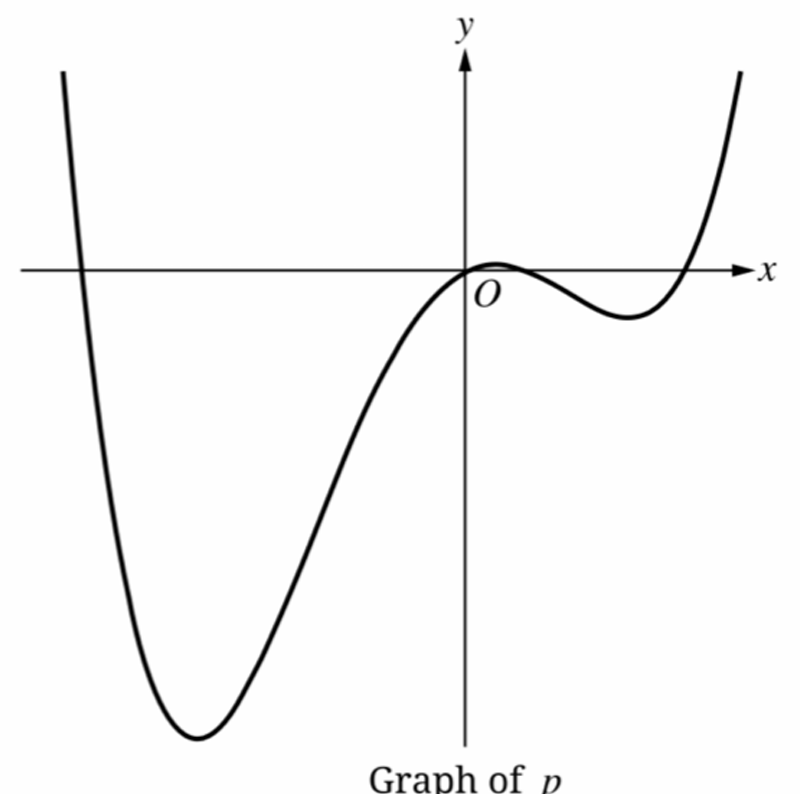
Question
▶️ Answer/Explanation
The correct option is (B) Two.
A point of inflection occurs where the concavity of the function changes (from concave up to concave down, or vice versa).
Observing the graph of the quartic polynomial \(p\):
1. The curve is concave up around the first local minimum on the left.
2. It changes to concave down around the local maximum near the origin. This change requires one point of inflection.
3. The curve changes back to concave up around the second local minimum on the right. This change requires a second point of inflection.
Therefore, there are exactly two points where the concavity changes.
Question (Calc allowed)
▶️ Answer/Explanation
The relationship \( g(x) = f^{-1}(x) \) implies that \( f(g(x)) = x \).
Substituting the given condition \( g(x) = -3x \) into this relationship, we get \( f(-3x) = x \).
Using the definition of \( f \), the equation becomes \( 4 \cdot 3^{(-3x – 2)} + 1 = x \).
Since \( 4 \cdot 3^{(-3x – 2)} \) is always positive, \( x \) must be greater than \( 1 \), eliminating option (A).
Testing option (B) with \( x = 1.016 \): \( 4 \cdot 3^{(-3(1.016) – 2)} + 1 = 4 \cdot 3^{-5.048} + 1 \).
Calculating the value: \( 4 \cdot (0.0039) + 1 \approx 1.0156 \), which is approximately \( 1.016 \).
Thus, the correct value is (B) 1.016.
Question
▶️ Answer/Explanation
Let $y = \sqrt{4 – x^2}$. Since $-2 \le x \le 0$, the range of $f(x)$ is $0 \le y \le 2$.
The domain of $f^{-1}(x)$ is the range of $f(x)$, which is $0 \le x \le 2$.
To find the inverse, swap $x$ and $y$: $x = \sqrt{4 – y^2}$.
Square both sides: $x^2 = 4 – y^2$, which simplifies to $y^2 = 4 – x^2$.
Solving for $y$, we get $y = \pm\sqrt{4 – x^2}$.
Since the original domain was $x \le 0$, the inverse must satisfy $y \le 0$.
Therefore, $f^{-1}(x) = -\sqrt{4 – x^2}$ for $0 \le x \le 2$.
The correct option is (C).
Question
(B) $f^{-1}(x) = \sqrt{\frac{x}{4} – 3}$ for $x \geq 0$
(C) $f^{-1}(x) = \sqrt{\frac{x-3}{4}}$ for $x \geq 3$
(D) $f^{-1}(x) = \frac{\sqrt{x-3}}{4}$ for $x \geq 3$
▶️ Answer/Explanation
Set $y = 4x^2 + 3$ and solve for $x$ to find the inverse.
Subtract $3$ from both sides: $y – 3 = 4x^2$.
Divide both sides by $4$: $\frac{y-3}{4} = x^2$.
Take the square root of both sides: $x = \sqrt{\frac{y-3}{4}}$ (since $x \geq 0$).
Swap $x$ and $y$: $f^{-1}(x) = \sqrt{\frac{x-3}{4}}$.
The range of $f(x)$ is $y \geq 3$, so the domain of $f^{-1}(x)$ is $x \geq 3$.
Therefore, the correct choice is (C).
Question
(A)
| \(x\) | \(g(x)\) |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 4 |
| 4 | 8 |
| 5 | 16 |
(B)
| \(x\) | \(g(x)\) |
|---|---|
| 1 | -20 |
| 2 | -10 |
| 3 | -5 |
| 4 | 5 |
| 5 | 10 |
(C)
| \(x\) | \(g(x)\) |
|---|---|
| 1 | 1 |
| 2 | 5 |
| 3 | 7 |
| 4 | 5 |
| 5 | 1 |
(D)
| \(x\) | \(g(x)\) |
|---|---|
| 1 | 7 |
| 2 | 3 |
| 3 | 1 |
| 4 | 3 |
| 5 | 7 |
▶️ Answer/Explanation
The correct option is (C).
For a function to be concave down, the slope (or rate of change) must be decreasing. In a table of values with equal \(x\)-steps, this means the first differences between consecutive \(g(x)\) values must get smaller as \(x\) increases.
Let’s calculate the first differences for each option:
Option (A): \(2-1=1\), \(4-2=2\), \(8-4=4\), \(16-8=8\). The rate is increasing (\(1, 2, 4, 8\)), so it is concave up.
Option (B): \(-10-(-20)=10\), \(-5-(-10)=5\), \(5-(-5)=10\). The rate fluctuates, so it is not consistently concave down.
Option (C): \(5-1=4\), \(7-5=2\), \(5-7=-2\), \(1-5=-4\). The rate is strictly decreasing (\(4, 2, -2, -4\)), which indicates the function is concave down.
Option (D): \(3-7=-4\), \(1-3=-2\), \(3-1=2\), \(7-3=4\). The rate is increasing (\(-4, -2, 2, 4\)), so it is concave up.
Question
(B) $3.894$ and $13.728$ only
(C) $5.911$ and $11.590$
(D) $3.894$, $8.627$, and $13.728$
▶️ Answer/Explanation
The function $R(d)$ represents the rate of change of $M(d)$, so $M'(d) = R(d)$.
Points of inflection for $M(d)$ occur where its second derivative $M”(d)$ changes sign.
Since $M”(d) = R'(d)$, we must find where $R(d)$ has relative extrema (slopes of zero and sign changes).
Differentiate $R(d)$ to get $R'(d) = \frac{1}{200}(-4d^3 + 105d^2 – 822d + 1845)$.
Set $R'(d) = 0$ and solve for $d$ using a graphing calculator or numerical methods.
The roots of $R'(d)$ are approximately $d \approx 3.894$, $d \approx 8.627$, and $d \approx 13.728$.
At each of these values, $R'(d)$ (the second derivative of $M$) changes sign.
Therefore, $M(d)$ has points of inflection at $d = 3.894, 8.627, \text{ and } 13.728$.
Correct Option: (D)
Question
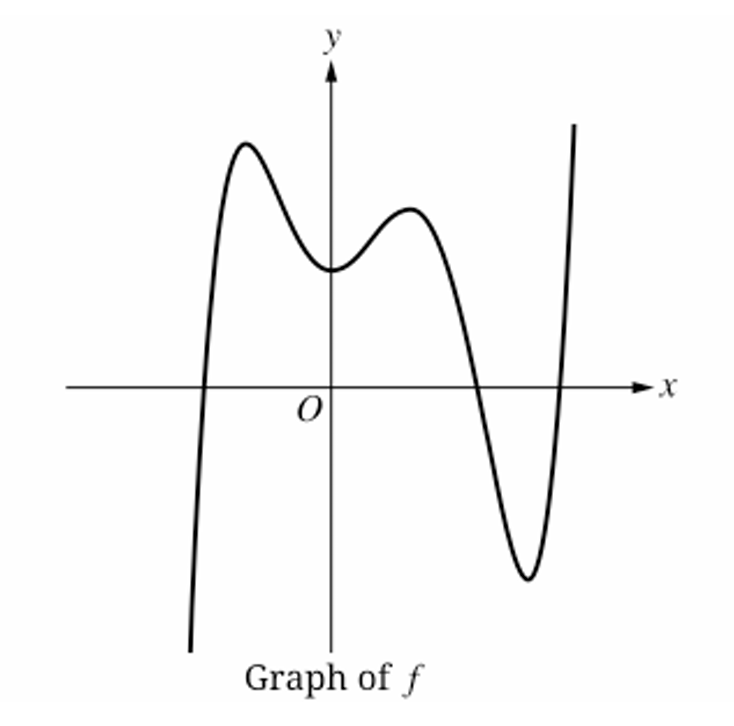
(B) Three
(C) Four
(D) Five
▶️ Answer/Explanation
A point of inflection occurs where the graph changes concavity (from concave up to concave down, or vice-versa).
Starting from the left, the graph begins concave down as it rises toward the first local maximum.
It switches to concave up to form the first local minimum near the $y$-axis (Point $1$).
It switches back to concave down to form the second local maximum (Point $2$).
It then switches to concave up to form the deep local minimum on the right (Point $3$).
Finally, it switches to concave down very briefly or stays concave up? Looking closely, the final upward stroke suggests a $4^{th}$ change in curvature (Point $4$).
Counting the transitions between the peaks and valleys, there are four distinct inflection points.
Correct Option: (C)
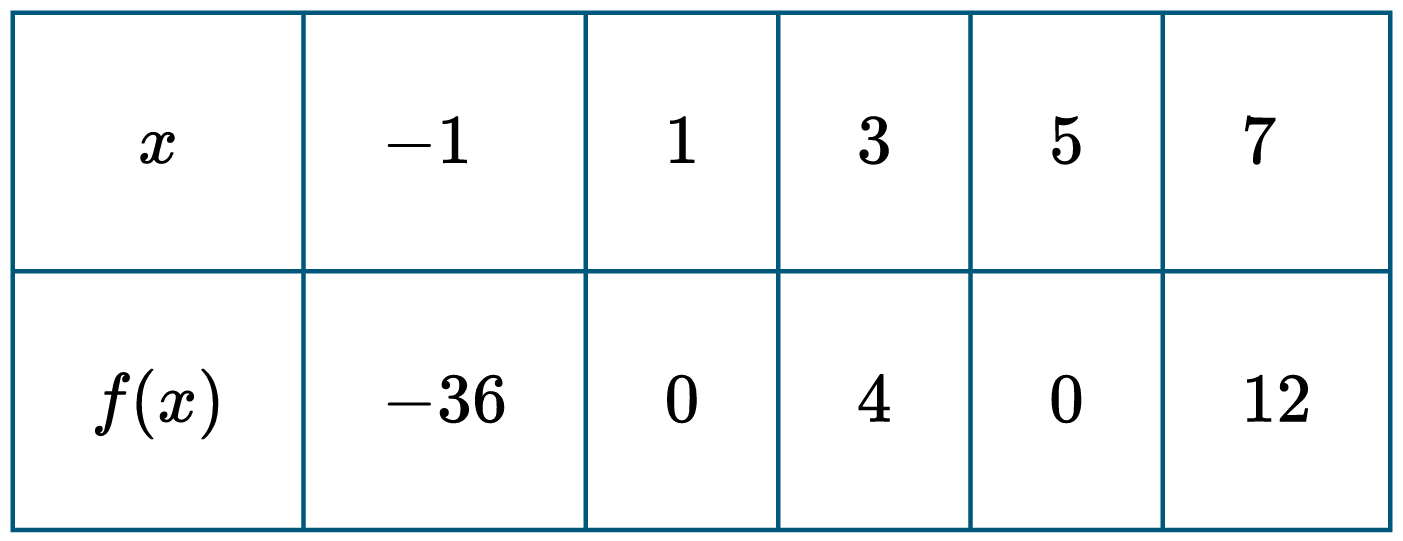
Question
▶️ Answer/Explanation
The table shows zeros at $x = 1$ and $x = 5$, where $f(1) = 0$ and $f(5) = 0$.
Between these zeros, at $x = 3$, the function is positive ($f(3) = 4$).
For $x < 1$, specifically at $x = -1$, the function is negative ($f(-1) = -36$).
For $x > 5$, specifically at $x = 7$, the function is positive ($f(7) = 12$).
Since $f(x)$ must cross or touch the x-axis only at $x=1$ and $x=5$, the sign change at $x=1$ (negative to positive) indicates it is not a maximum.
However, at $x = 5$, the function goes from positive ($f(3)=4$) to zero ($f(5)=0$) and back to positive ($f(7)=12$).
This means $f(x)$ touches the x-axis at $(5, 0)$ without crossing it, staying $\ge 0$ in that interval.
Therefore, $(5, 0)$ must be a local minimum.
Question
▶️ Answer/Explanation
The “rate of change” of $g$ refers to the first derivative, $g'(x)$.
If $g'(x)$ is increasing for $x < 2$, then the second derivative $g”(x) > 0$.
A positive second derivative ($g”(x) > 0$) means the graph is concave up.
If $g'(x)$ is decreasing for $x > 2$, then the second derivative $g”(x) < 0$.
A negative second derivative ($g”(x) < 0$) means the graph is concave down.
Since the concavity changes at $x = 2$, there is a point of inflection at $x = 2$.
Therefore, the correct choice is (D).
Question
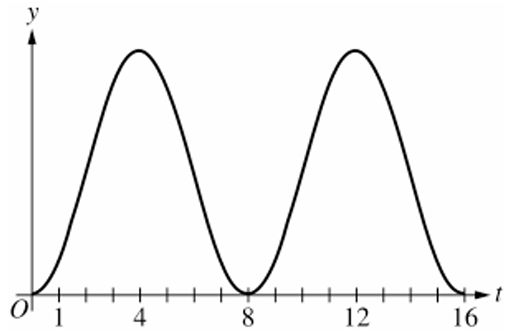
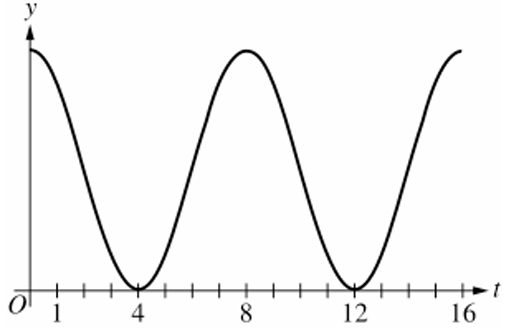
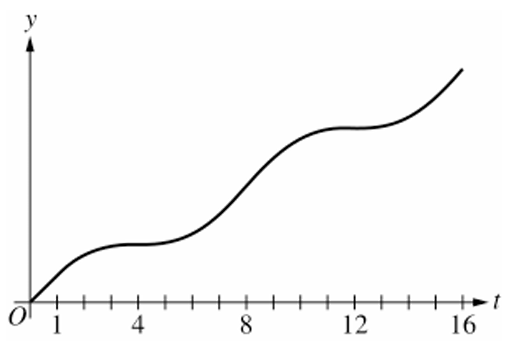
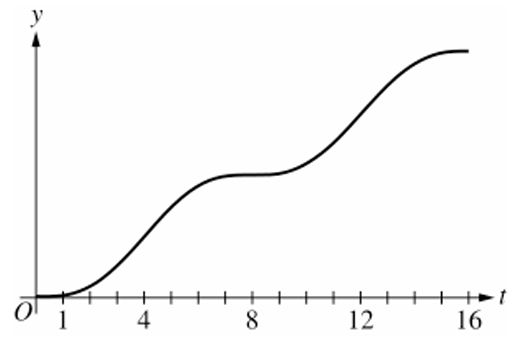
▶️ Answer/Explanation
The function $N(t)$ represents the total number of customers, so $N(t) = \int_{0}^{t} R(x) dx$.
Since $R(t)$ is a rate of arrival, $R(t) \ge 0$, which means $N(t)$ must be a non-decreasing function.
The derivative of the total accumulation is the rate, so $N'(t) = R(t)$ and $N”(t) = R'(t)$.
When $R(t)$ is increasing ($0 < t < 4$ and $8 < t < 12$), $N(t)$ is concave up ($N”(t) > 0$).
When $R(t)$ is decreasing ($4 < t < 8$ and $12 < t < 16$), $N(t)$ is concave down ($N”(t) < 0$).
Graph (D) starts at $(0,0)$, always increases, and switches concavity at $t = 4, 8, 12$.
Therefore, the correct graph is (D).
Question
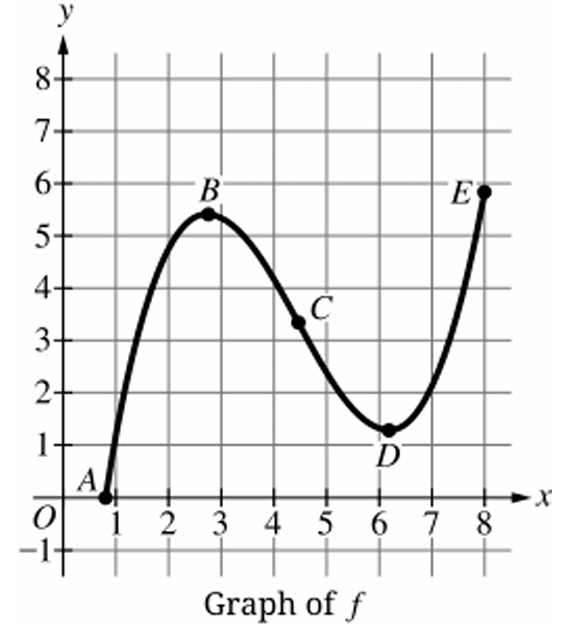
▶️ Answer/Explanation
(A) The interval from \( A \) to \( B \)
1. A function is increasing where \( f'(x) > 0 \), meaning the graph rises from left to right.
2. From \( A \) to \( B \), the graph rises to a local maximum at \( B \), so \( f'(x) > 0 \).
3. The point \( C \) is labeled as the point of inflection, so concavity changes at \( C \).
4. Therefore, for all \( x < C \), the graph is concave down (\( f”(x) < 0 \)).
5. Since the interval \( A \) to \( B \) lies entirely before \( C \), it is concave down.
6. Hence, \( f \) is increasing and concave down on \( (A, B) \).
Question
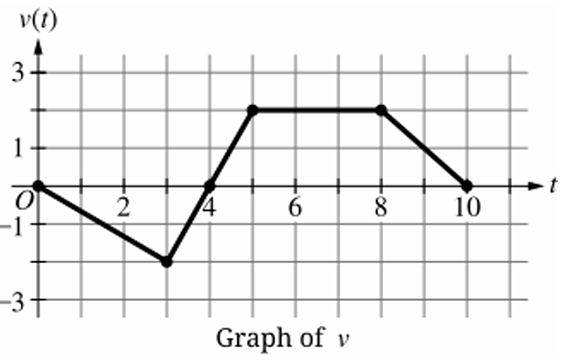
▶️ Answer/Explanation
(D) \(0 < t < 3\) and \(8 < t < 10\)
Velocity is decreasing where the graph of \(v(t)\) has a negative slope. From \(t=0\) to \(t=3\), the graph slopes downward continuously. From \(t=3\) to \(t=5\), the slope is positive (velocity increasing). From \(t=5\) to \(t=8\), the slope is zero (constant velocity). From \(t=8\) to \(t=10\), the slope is negative again. Therefore, velocity decreases only on \(0 < t < 3\) and \(8 < t < 10\).
1. Velocity decreases when the slope of \(v(t)\) is negative.
2. From \(0 < t < 3\), the line segment slopes downward ⇒ decreasing.
3. From \(3 < t < 5\), the slope is positive ⇒ increasing.
4. From \(5 < t < 8\), the slope is \(0\) ⇒ constant velocity.
5. From \(8 < t < 10\), the slope is negative ⇒ decreasing.
6. Hence, the correct intervals are \(0 < t < 3\) and \(8 < t < 10\).
Question
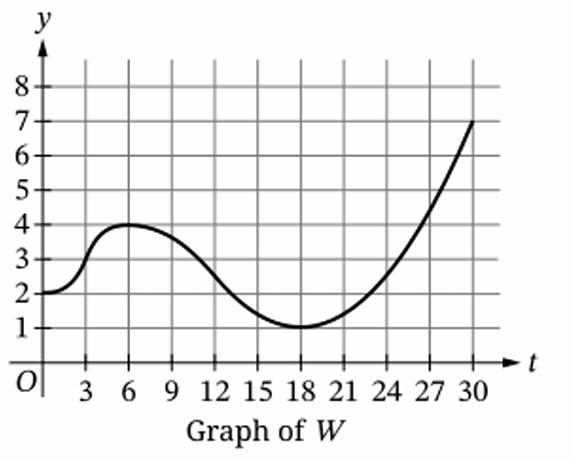
(B) \( (3,12) \)
(C) \( (0,3) \) and \( (18,30) \) only
(D) \( (0,6) \) and \( (18,30) \)
▶️ Answer/Explanation
(A) \( (3,6) \) only
2. Thus the graph must be increasing and concave down.
3. From \( t = 0 \) to \( t = 6 \), the function increases.
4. However, from \( (0,3) \), the slope increases (concave up).
5. From \( (3,6) \), the slope decreases to \( 0 \) (concave down).
6. From \( (18,30) \), the function increases but is concave up.
7. Therefore, the only interval satisfying both conditions is \( (3,6) \).
Question
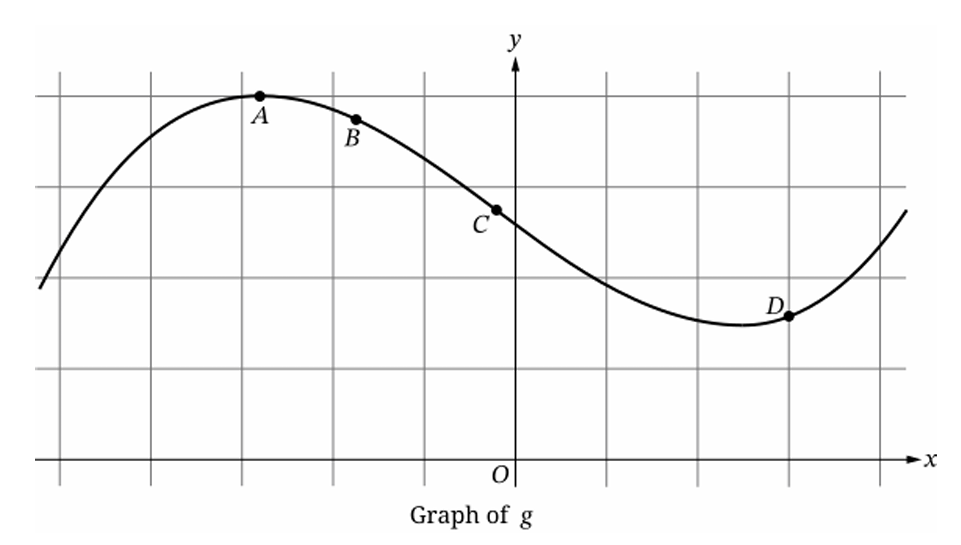
▶️ Answer/Explanation
(C)
1. The rate of change of \( g \) at a point is the slope \( g'(x) \).
2. At \( A \), a relative maximum, \( g'(A) = 0 \).
3. At \( D \), near a minimum, the slope is approximately \( 0 \) (slightly positive).
4. At \( B \), the function is decreasing, so \( g'(B) < 0 \), but not steepest.
5. At \( C \), the only point of inflection, the graph changes concavity.
6. At an inflection point on a decreasing curve, the slope is most negative.
7. Therefore, \( g'(C) \) is the smallest (least) value.
8. Hence, the rate of change is least at \( C \).
Question
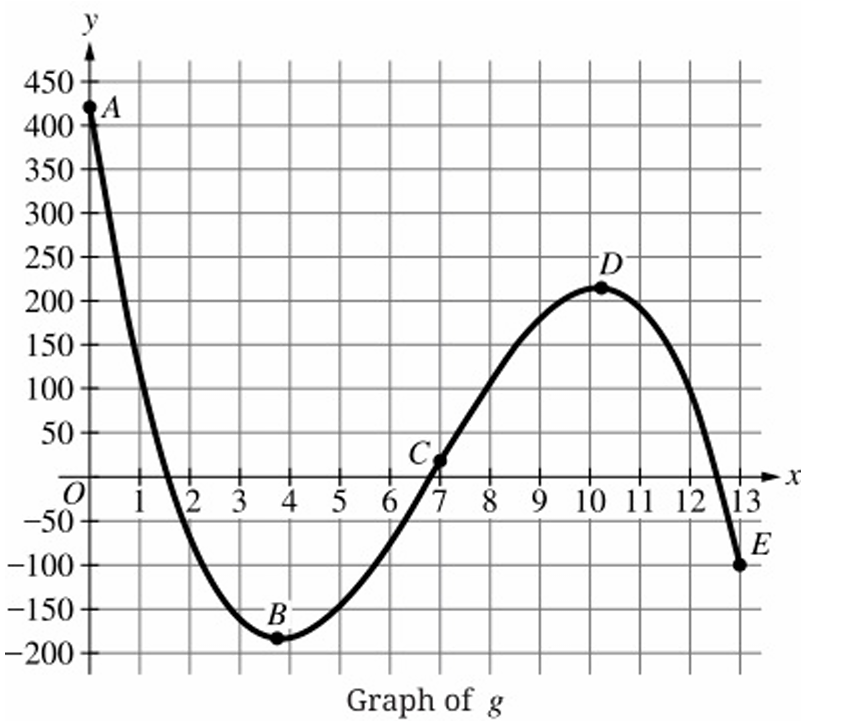
▶️ Answer/Explanation
(D) \( [t_C, t_D] \) and \( [t_D, t_E] \)
1. The rate of change of \( g \) is \( g'(x) \). It is decreasing where \( g”(x) < 0 \).
2. \( g”(x) < 0 \) corresponds to the graph being concave down.
3. The graph has exactly one inflection point at \( C \), so concavity changes only at \( t_C \).
4. From \( t_A \) to \( t_C \), the graph is concave up (slope increasing).
5. From \( t_C \) to \( t_E \), the graph is concave down (slope decreasing).
6. Therefore, the rate of change of \( g \) is decreasing on \( [t_C, t_D] \) and \( [t_D, t_E] \).
7. Hence, the correct answer is (D).
Question

▶️ Answer/Explanation
The correct answer is (B) 3.
From the table, we identify the extrema for \(x \ge 0\). The function decreases to a minimum value of \(f(2) = -3\) and then increases to a value of \(f(4) = 2\).
Since \(f\) is an odd function, it satisfies the property \(f(-x) = -f(x)\). This means the graph is symmetric with respect to the origin.
A local minimum on the positive side corresponds to a local maximum on the negative side. Therefore, the minimum at \(x = 2\) implies a maximum at \(x = -2\) given by \(f(-2) = -f(2) = -(-3) = 3\).
We must also check the endpoints. We know \(f(4) = 2\), which implies \(f(-4) = -f(4) = -2\).
Comparing the highest points on the entire domain \([-4, 4]\): the maximum value at \(x=4\) is \(2\), and the maximum value at \(x=-2\) is \(3\).
Thus, the absolute maximum value of \(f\) is \(3\).
Question
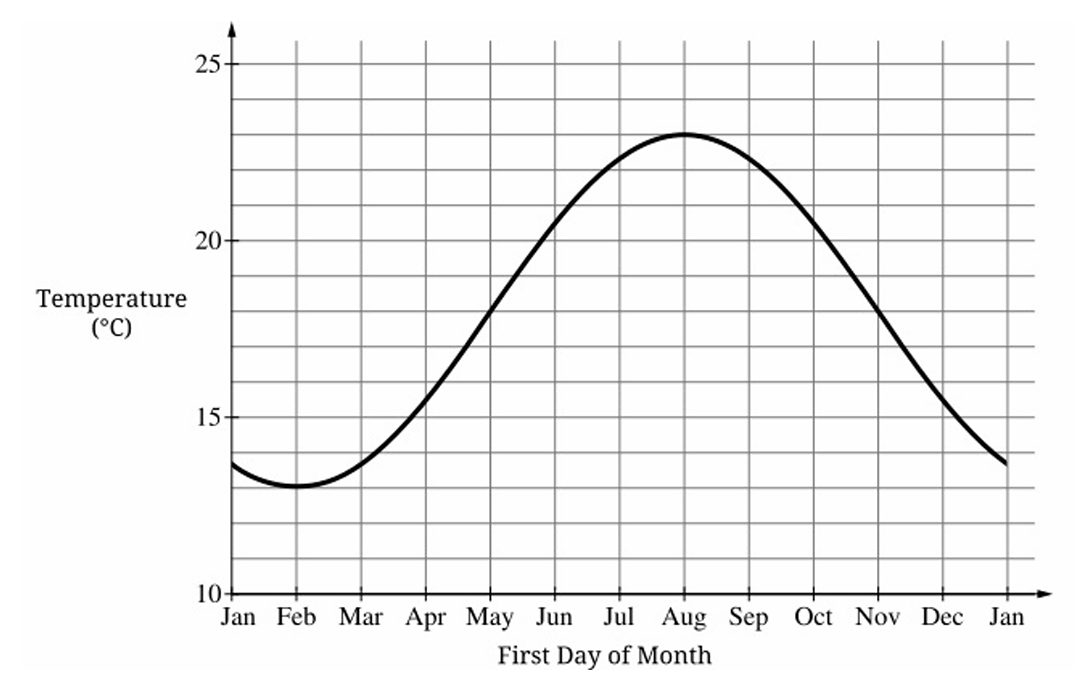
▶️ Answer/Explanation
(B) May
The rate of change corresponds to the slope of the temperature curve. The greatest rate of change occurs where the graph is increasing most steeply. From the graph, the temperature rises most rapidly during the spring months. Around May, the curve has its steepest positive slope. In February the slope is small and slightly negative, in August the slope is approximately \(0\) (near maximum), and in November the slope is negative. Therefore, the greatest rate of change occurs in May.
1. The rate of change equals the derivative, represented by the slope of the tangent line.
2. We look for the point where the curve is steepest upward (maximum positive slope).
3. In February, the graph is near a minimum, so slope \(\approx 0\).
4. In May, the graph is increasing rapidly, giving the largest positive slope.
5. In August, the graph is near a maximum, so slope \(\approx 0\).
6. In November, the graph is decreasing, so slope is negative.
7. Hence, the greatest rate of change occurs in May.
Question
▶️ Answer/Explanation
We analyze the definitions of \(g\) and \(h\) to determine the properties of \(f\).
1. We are given \(h(x) = g(x+1) – g(x) = -6\). Since the difference is negative, \(g(x+1) < g(x)\), which means \(g\) is strictly decreasing.
2. The function \(g(x)\) represents the first difference (approximate slope) of \(f(x)\), and \(h(x)\) represents the second difference of \(f(x)\).
3. In calculus, a constant negative second difference (like \(h(x) = -6\)) indicates that the function \(f\) is concave down (like an inverted parabola, \(y = -3x^2\)).
4. While \(f\) is concave down, it does not necessarily always have a negative slope (e.g., the left side of an inverted parabola has a positive slope).
5. Therefore, the only statements that must be true are that \(g\) is decreasing and \(f\) is concave down.
Conclusion: This corresponds to option (D).
Question
▶️ Answer/Explanation
Question
Most-appropriate topic codes (CED):
• TOPIC 3.10: Trigonometric Equations and Inequalities — part (B)
• TOPIC 1.1: Change in Tandem — part (C)
▶️ Answer/Explanation
(A)
First, determine the physical parameters of the clock to find the sinusoidal constants.
The diameter is (24) inches, so the radius is (12) inches. This corresponds to the amplitude, (a = 12).
The center of the clock is (5) feet above the ground, which converts to (60) inches. This is the midline, (d = 60).
The second hand completes a cycle every (30) seconds. The period is (30), so the frequency coefficient is (b = \dfrac{2\pi}{30} = \dfrac{\pi}{15}).
At (t = 0), the hand is pointing straight up (maximum height). Since the cosine function starts at a maximum, there is no phase shift, so (c = 0).
Thus, the function is:
(h(t) = 12 \cos\left( \dfrac{\pi}{15} t \right) + 60)
(B)
Set \(h(t)\) equal to the given height and solve for \(t\):
\(12 \cos\left( \dfrac{\pi}{15} t \right) + 60 = 72 – 6\sqrt{2}\)
\(12 \cos\left( \dfrac{\pi}{15} t \right) = 12 – 6\sqrt{2}\)
\(\cos\left( \dfrac{\pi}{15} t \right) = 1 – \dfrac{\sqrt{2}}{2} = \dfrac{2 – \sqrt{2}}{2}\)
Let \(\theta = \dfrac{\pi}{15} t\). We need to solve \(\cos \theta = \dfrac{2 – \sqrt{2}}{2}\).
\(\theta = \pm \arccos\left( \dfrac{2 – \sqrt{2}}{2} \right) + 2\pi k\).
For the interval \(0 < t \leq 30\), we look for solutions in \((0, 2\pi]\).
The two solutions for \(\theta\) are \(\theta_1 = \arccos\left( \dfrac{2 – \sqrt{2}}{2} \right)\) and \(\theta_2 = 2\pi – \theta_1\).
Converting back to time \(t = \dfrac{15}{\pi} \theta\):
\(t_1 = \dfrac{15}{\pi} \arccos\left( \dfrac{2 – \sqrt{2}}{2} \right)\) and \(t_2 = 30 – t_1\).
(C) i.
Yes, the graph of \(h(t)\) has points of inflection. The function \(h(t)\) is a smooth, continuous cosine wave.
Points of inflection on a sinusoidal graph occur where the graph crosses its midline (concavity changes from up to down or vice versa). This happens when:
\(\cos\left( \dfrac{\pi}{15} t \right) = 0\)
\(\dfrac{\pi}{15} t = \dfrac{\pi}{2} + k\pi\)
\(t = 15\left( \dfrac{1}{2} + k \right) = 7.5 + 15k\)
For the interval \(0 \leq t \leq 30\):
If \(k=0\), \(t = 7.5\).
If \(k=1\), \(t = 22.5\).
The points of inflection are at \(t = 7.5\) seconds and \(t = 22.5\) seconds.
(C) ii.
In this context:
The rate of change represents the vertical velocity of the tip of the second hand.
The rate the rate is changing represents the vertical acceleration.
A point of inflection occurs where the concavity changes, which means the vertical acceleration is transitioning from positive to negative (or vice versa) and is instantaneously zero. Physically, these are the moments when the tip of the second hand is at the same height as the center of the clock (midline). At these specific points, the vertical speed (rate of change) is at its absolute maximum magnitude.
Question
▶️ Answer/Explanation
a. Graphing the function
Using a graphing utility for \(P(x) = -0.0013x^3 + 0.3507x^2 – 0.4591x – 421.888\) on the interval \([0, 200]\) reveals a cubic curve shape.
The graph starts with a slight dip to a local minimum near \(x=0\), then rises steeply to a local maximum near \(x=180\), before falling again.
b. Average rate of change between extrema
First, find the derivative: \(P'(x) = -0.0039x^2 + 0.7014x – 0.4591\).
Set \(P'(x) = 0\) and use the quadratic formula to find the extrema: \(x \approx 0.66\) (local min) and \(x \approx 179.19\) (local max).
Calculate the profit at these points: \(P(0.66) \approx -422.04\) and \(P(179.19) \approx 3276.57\).
The average rate of change is: \(\frac{3276.57 – (-422.04)}{179.19 – 0.66} = \frac{3698.61}{178.53} \approx 20.72\).
c. Equation of the secant line
The slope \(m\) was found in part (b) to be approximately \(20.72\).
Using the point-slope form \(y – y_1 = m(x – x_1)\) with the minimum point \((0.66, -422.04)\):
\(y – (-422.04) = 20.72(x – 0.66)\)
\(y = 20.72x – 13.68 – 422.04\)
The equation is approximately \(y = 20.72x – 435.72\).
d. Inflection point
Find the second derivative: \(P”(x) = -0.0078x + 0.7014\).
Set \(P”(x) = 0\) to find the change in concavity: \(0 = -0.0078x + 0.7014 \Rightarrow x = \frac{0.7014}{0.0078} \approx 89.92\).
Find the corresponding y-value: \(P(89.92) \approx 1427.27\).
The inflection point is approximately \((89.92, 1427.27)\).
e. Variation of rate of change
The rate of change is represented by the derivative, \(P'(x)\).
Before the inflection point (\(x < 89.92\)), the graph is concave up (\(P”(x) > 0\)), so the rate of change is increasing.
After the inflection point (\(x > 89.92\)), the graph is concave down (\(P”(x) < 0\)), so the rate of change is decreasing.