AP Precalculus -1.4 Polynomial Functions and Rates of Change- Study Notes - Effective Fall 2023
AP Precalculus -1.4 Polynomial Functions and Rates of Change- Study Notes – Effective Fall 2023
AP Precalculus -1.4 Polynomial Functions and Rates of Change- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Identify key characteristics of polynomial functions related to rates of change.
Key Concepts:
Polynomial Functions
Local and Global Extrema of Polynomial Functions
Local Extrema Between Zeros of Polynomial Functions
Global Extrema of Even-Degree Polynomial Functions
Points of Inflection of Polynomial Functions
Polynomial Functions
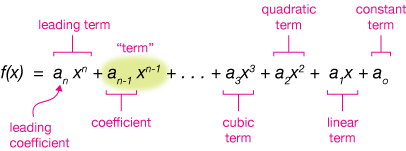
A polynomial function in the variable \( x \) is a function that can be written in the analytical form
\( p(x) = a_n x^n + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + \dots + a_2 x^2 + a_1 x + a_0 \)
Here, \( n \) is a positive integer, each coefficient \( a_i \) is a real number, and the leading coefficient \( a_n \) is nonzero.
Degree of a Polynomial
The degree of a polynomial is the highest power of \( x \) with a nonzero coefficient. For the function above, the degree is \( n \).
Leading Term and Leading Coefficient
The leading term of a polynomial is the term with the highest power of \( x \), which is \( a_n x^n \).
The leading coefficient is the coefficient of the leading term, which is \( a_n \).
Constant Polynomial
A constant function such as \( f(x) = 7 \) is also a polynomial function. It has degree zero because it can be written as \( 7 = 7x^0 \).
Example:
Consider the polynomial \( p(x) = 4x^3 – 2x^2 + 7x – 5 \).
▶️ Answer/Explanation
Degree
The highest power of \( x \) is 3, so the degree is 3.
Leading term
The leading term is \( 4x^3 \).
Leading coefficient
The leading coefficient is 4.
Example:
Determine whether the function \( f(x) = -3 \) is a polynomial function. If so, state its degree.
▶️ Answer/Explanation
The function \( f(x) = -3 \) can be written as \( -3x^0 \).
Therefore, it is a polynomial function.
Since the highest power of \( x \) is 0, the degree of the polynomial is 0.
Local and Global Extrema of Polynomial Functions
A polynomial function can change behavior over its domain, switching between increasing and decreasing.
At a point where the function changes from increasing to decreasing, or from decreasing to increasing, the function attains a local (or relative) extreme value.
Local Maximum and Local Minimum
A local maximum occurs at an input value where the function output is greater than the outputs at nearby input values.
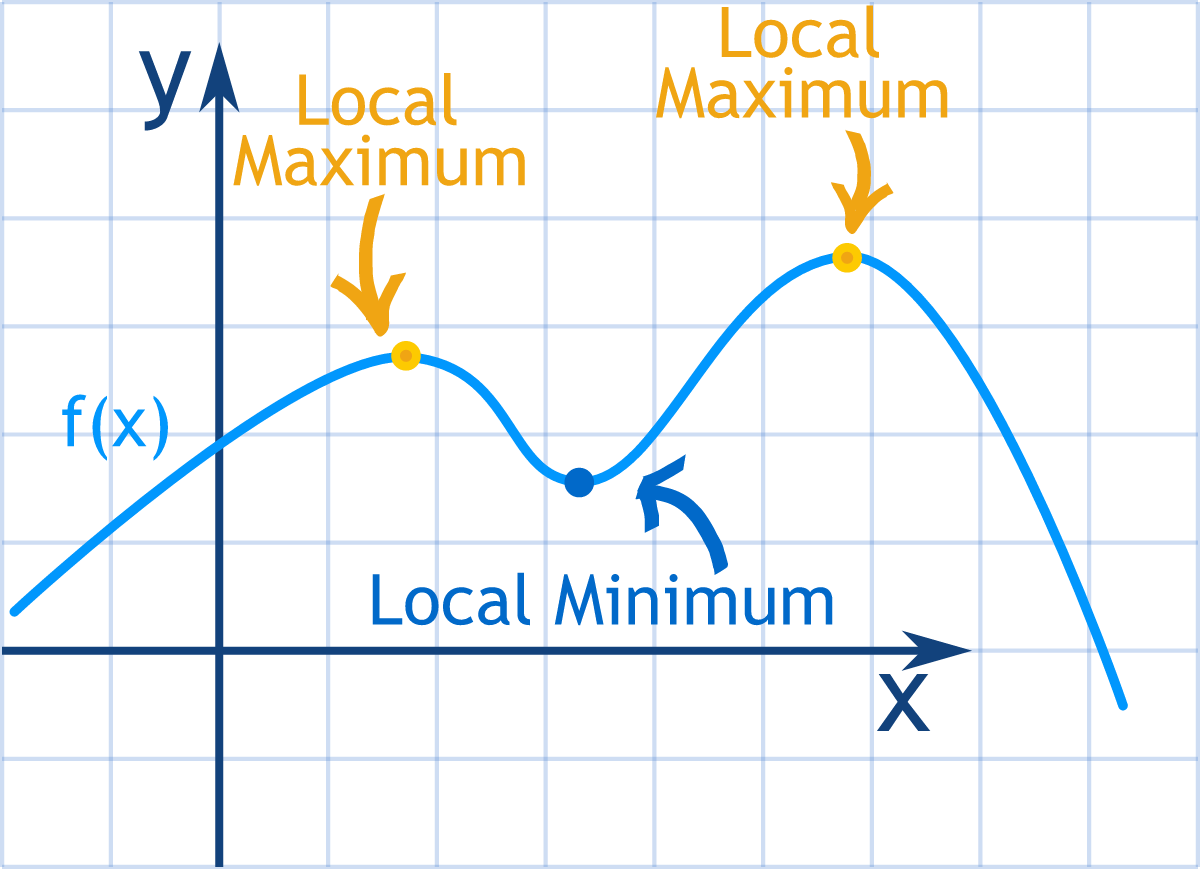
A local minimum occurs at an input value where the function output is less than the outputs at nearby input values.
Local extrema can also occur at included endpoints of a polynomial function when the domain is restricted.
Global (Absolute) Maximum and Minimum
Among all local maximum values, the greatest output value is called the global or absolute maximum.
Among all local minimum values, the smallest output value is called the global or absolute minimum.
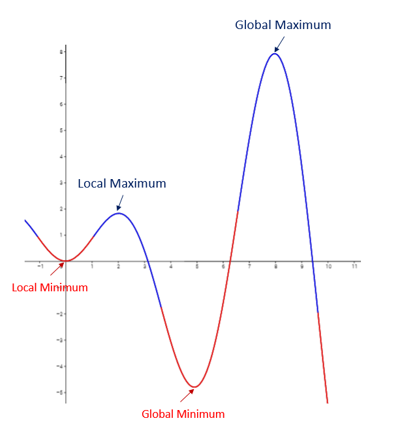
Global extrema represent the highest and lowest output values of the function over its entire domain.
Example:
Consider the function \( f(x) = -x^2 + 4x + 1 \).
Identify any local or global extrema.
▶️ Answer/Explanation
This is a quadratic function that opens downward.
A downward opening parabola has a maximum value at its vertex.
The vertex occurs at \( x = \dfrac{-b}{2a} = \dfrac{-4}{2(-1)} = 2 \).
\( f(2) = -4 + 8 + 1 = 5 \).
Conclusion
The function has a local maximum of 5 at \( x = 2 \), which is also the global maximum.
Example:
Let \( g(x) = x^3 – 3x^2 + 2 \) on the restricted domain \( 0 \le x \le 3 \).
Identify the local and global extrema.
▶️ Answer/Explanation
The function changes from increasing to decreasing at \( x = 2 \).
\( g(2) = 8 – 12 + 2 = -2 \).
This is a local minimum.
Evaluate the endpoints:
\( g(0) = 2 \)
\( g(3) = 27 – 27 + 2 = 2 \)
Conclusion
The local minimum is \( -2 \) at \( x = 2 \).
The global maximum is \( 2 \) at both endpoints \( x = 0 \) and \( x = 3 \).
Local Extrema Between Zeros of Polynomial Functions
A nonconstant polynomial function is continuous for all real input values.
Because of this continuity, whenever a polynomial has two distinct real zeros, the function must change direction between those zeros.
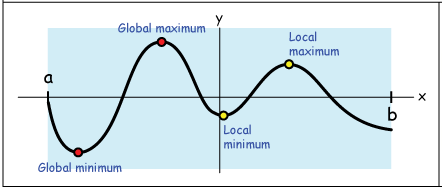
As a result, between every pair of distinct real zeros, there must be at least one input value where the function has a local maximum or a local minimum.
At this point, the function switches between increasing and decreasing behavior.
This property helps explain the shape of polynomial graphs and limits how often a polynomial can cross the x-axis.
Example:
Consider the polynomial \( f(x) = x^2 – 4 \).
Explain why there must be a local extremum between its real zeros.
▶️ Answer/Explanation
Find the zeros of the function.
\( x^2 – 4 = 0 \Rightarrow x = -2 \text{ and } x = 2 \)
Between \( x = -2 \) and \( x = 2 \), the graph changes direction.
The vertex occurs at \( x = 0 \), where the function has a local minimum.
Therefore, there is a local extremum between the two distinct real zeros.
Example:
The polynomial \( g(x) = x^3 – 3x \) has real zeros at \( x = -\sqrt{3} \), \( x = 0 \), and \( x = \sqrt{3} \).
Explain how this guarantees the existence of local extrema.
▶️ Answer/Explanation
There are two intervals between distinct real zeros:
Between \( -\sqrt{3} \) and \( 0 \)
Between \( 0 \) and \( \sqrt{3} \)
In each interval, the polynomial must change direction.
Therefore, the graph has at least one local maximum or local minimum between each pair of distinct real zeros.
Global Extrema of Even-Degree Polynomial Functions
A polynomial function of even degree is a polynomial whose highest power of the variable is an even integer, such as 2, 4, or 6.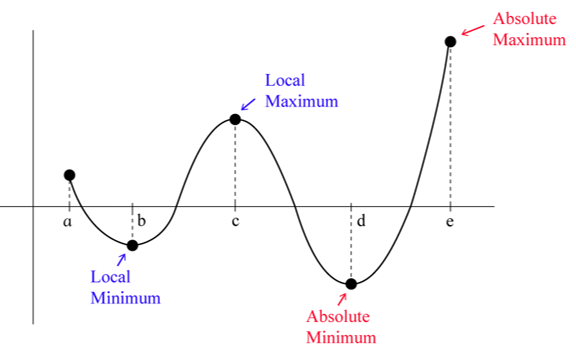
For an even-degree polynomial function, the graph will always have both ends going in the same direction.
As a result, every even-degree polynomial must have either:
a global (absolute) minimum, or
a global (absolute) maximum.
Which one occurs depends on the leading coefficient of the polynomial.
If the leading coefficient is positive, the graph opens upward and has a global minimum.
If the leading coefficient is negative, the graph opens downward and has a global maximum.
Example:
Consider the polynomial \( f(x) = x^2 – 4x + 5 \).
Determine whether the function has a global maximum or a global minimum.
▶️ Answer/Explanation
This is a quadratic function, so it has even degree.
The leading coefficient is positive, so the graph opens upward.
Therefore, the function has a global minimum.
The vertex occurs at \( x = \dfrac{-b}{2a} = \dfrac{4}{2} = 2 \).
\( f(2) = 4 – 8 + 5 = 1 \).
Conclusion
The function has a global minimum value of 1 at \( x = 2 \).
Example:
Consider the polynomial \( g(x) = -2x^4 + 3x^2 – 1 \).
Explain why the function has a global maximum.
▶️ Answer/Explanation
The highest power of \( x \) is 4, which is even.
The leading coefficient is negative.
This means the graph opens downward on both ends.
Therefore, the function must attain a global maximum value.
Points of Inflection of Polynomial Functions
A point of inflection of a polynomial function occurs at an input value where the behavior of the rate of change switches.
Specifically, at a point of inflection, the rate of change of the function changes from increasing to decreasing, or from decreasing to increasing.
This corresponds to a change in the concavity of the graph.
A point of inflection occurs where the graph changes:
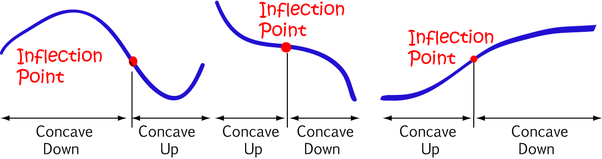
from concave up to concave down, or
from concave down to concave up.
At an inflection point, the function does not necessarily have a maximum or minimum.
Example:
Consider the polynomial \( f(x) = x^3 \).
Identify and explain the point of inflection.
▶️ Answer/Explanation
For \( x < 0 \), the graph of \( f(x) = x^3 \) is concave down.
For \( x > 0 \), the graph is concave up.
The concavity changes at \( x = 0 \).
Therefore, \( (0, 0) \) is a point of inflection.
Example:
Consider the polynomial \( g(x) = x^3 – 3x^2 + 2 \).
Explain where a point of inflection occurs.
▶️ Answer/Explanation
The graph is concave up for larger values of \( x \) and concave down for smaller values of \( x \).
The change in concavity occurs at \( x = 1 \).
Therefore, the function has a point of inflection at \( x = 1 \).
