AP Precalculus -1.6 Polynomial Functions and End Behavior- Study Notes - Effective Fall 2023
AP Precalculus -1.6 Polynomial Functions and End Behavior- Study Notes – Effective Fall 2023
AP Precalculus -1.6 Polynomial Functions and End Behavior- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Describe end behaviors of polynomial functions.
Key Concepts:
- End Behavior of Polynomial Functions as \( x \to \infty \)
- End Behavior of Polynomial Functions as \( x \to -\infty \)
- How the Leading Term Determines End Behavior
End Behavior of Polynomial Functions as \( x \to \infty \)
A nonconstant polynomial function has output values that grow without bound as the input values increase without bound.
As \( x \to \infty \), the values of a polynomial function \( p(x) \) will either: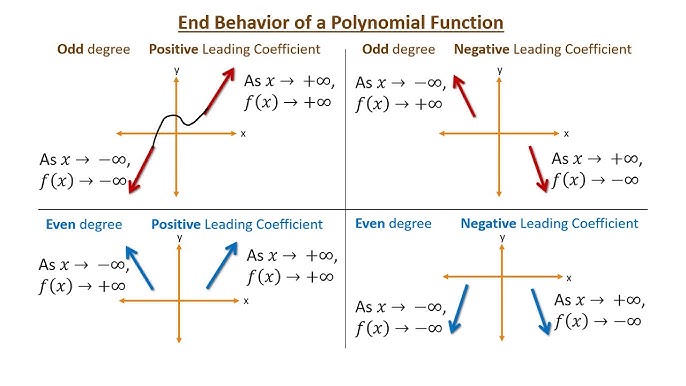
increase without bound, or
decrease without bound.
This behavior is called the end behavior of the polynomial.
Mathematically, this is written using limits as:
\( \lim_{x \to \infty} p(x) = \infty \)
or
\( \lim_{x \to \infty} p(x) = -\infty \)
The end behavior of a polynomial is determined by its leading term, which is the term with the highest power of \( x \).
Specifically, the degree of the polynomial and the sign of the leading coefficient determine whether the function increases or decreases as \( x \to \infty \).
Example:
Describe the end behavior of the polynomial \( p(x) = 2x^3 – 5x + 1 \).
▶️ Answer/Explanation
The leading term of the polynomial is \( 2x^3 \).
As \( x \to \infty \), the term \( 2x^3 \) dominates all other terms.
Since the leading coefficient is positive and the degree is odd, the function increases without bound.
Conclusion
\( \lim_{x \to \infty} p(x) = \infty \).
Example:
Describe the end behavior of the polynomial \( f(x) = -x^4 + 3x^2 – 7 \).
▶️ Answer/Explanation
The leading term is \( -x^4 \).
As \( x \to \infty \), the term \( -x^4 \) dominates the behavior of the function.
Because the leading coefficient is negative and the degree is even, the function decreases without bound.
Conclusion
\( \lim_{x \to \infty} f(x) = -\infty \).
End Behavior of Polynomial Functions as \( x \to -\infty \)
A nonconstant polynomial function has output values that grow without bound as the input values decrease without bound.
As \( x \to -\infty \), the values of a polynomial function \( p(x) \) will either:
increase without bound, or
decrease without bound.
This behavior is also part of the end behavior of the polynomial.
Mathematically, this behavior is written using limits as:
\( \lim_{x \to -\infty} p(x) = \infty \)
or
\( \lim_{x \to -\infty} p(x) = -\infty \)
As with \( x \to \infty \), the end behavior as \( x \to -\infty \) is determined by the leading term of the polynomial.
The parity of the degree (even or odd) and the sign of the leading coefficient together determine whether the function rises or falls as \( x \to -\infty \).
Example:
Describe the end behavior of the polynomial \( p(x) = 3x^5 – 2x^2 + 1 \) as \( x \to -\infty \).
▶️ Answer/Explanation
The leading term is \( 3x^5 \).
As \( x \to -\infty \), \( x^5 \to -\infty \).
Multiplying by the positive coefficient 3 keeps the sign negative.
Conclusion
\( \lim_{x \to -\infty} p(x) = -\infty \).
Example:
Describe the end behavior of the polynomial \( f(x) = -2x^4 + x – 6 \) as \( x \to -\infty \).
▶️ Answer/Explanation
The leading term is \( -2x^4 \).
As \( x \to -\infty \), \( x^4 \to \infty \).
Multiplying by the negative coefficient results in large negative values.
Conclusion
\( \lim_{x \to -\infty} f(x) = -\infty \).
How the Leading Term Determines End Behavior
The end behavior of a polynomial function describes how the output values behave as the input values increase or decrease without bound.
For a polynomial function \( p(x) \), the degree and the sign of the leading coefficient completely determine the end behavior.
This is because as \( x \to \infty \) or \( x \to -\infty \), the leading term dominates all lower-degree terms.
If the polynomial is written as
\( p(x) = a_n x^n + a_{n-1} x^{n-1} + \dots + a_1 x + a_0 \)
then for large values of \( |x| \), the behavior of \( p(x) \) is governed by the leading term \( a_n x^n \).
All other terms become insignificant compared to \( a_n x^n \) as \( x \) increases or decreases without bound.
Summary of End Behavior of Polynomial Functions
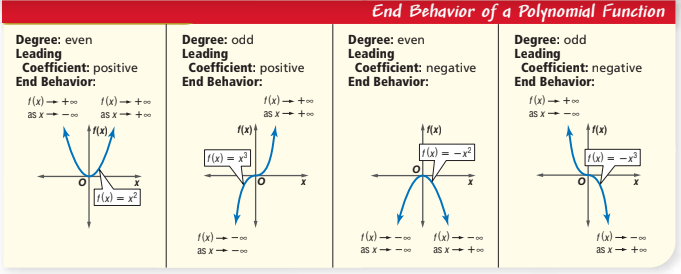
| Degree of Polynomial | Sign of Leading Coefficient | End Behavior as \( x \to -\infty \) | End Behavior as \( x \to \infty \) |
|---|---|---|---|
| Even | Positive | Rises | Rises |
| Even | Negative | Falls | Falls |
| Odd | Positive | Falls | Rises |
| Odd | Negative | Rises | Falls |
This table shows how the degree and the sign of the leading coefficient determine the end behavior of a polynomial function.
Example:
Determine the end behavior of the polynomial \( p(x) = -4x^6 + 3x^2 – 1 \).
▶️ Answer/Explanation
The leading term is \( -4x^6 \).
The degree is even and the leading coefficient is negative.
As \( x \to \infty \), \( p(x) \to -\infty \).
As \( x \to -\infty \), \( p(x) \to -\infty \).
Conclusion
Both ends of the graph fall.
Example:
Describe the end behavior of the polynomial \( f(x) = 5x^3 – x + 2 \).
▶️ Answer/Explanation
The leading term is \( 5x^3 \).
The degree is odd and the leading coefficient is positive.
As \( x \to -\infty \), \( f(x) \to -\infty \).
As \( x \to \infty \), \( f(x) \to \infty \).
Conclusion
The graph falls to the left and rises to the right.
