AP Precalculus -1.7 Rational Functions and End Behavior- MCQ Exam Style Questions - Effective Fall 2023

AP Precalculus -1.7 Rational Functions and End Behavior- MCQ Exam Style Questions – Effective Fall 2023

AP Precalculus -1.7 Rational Functions and End Behavior- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.

AP Precalculus – MCQ Exam Style Questions- All Topics

Question

The rational function $ r $ is given by $ r(x) = \frac{x^3 + 8x^2 + 17x + 10}{x^2 + 2x} = \frac{(x+1)(x+2)(x+5)}{x^2 + 2x} $. Which of the following gives equations for all the horizontal asymptotes, vertical asymptotes, and slant asymptotes of the graph of $ r $?

(A) $ x = 0 $ and $ y = x + 6 $
(B) $ x = 0 $ and $ x = -2 $
(C) $ x = 0 $ and $ y = 5x + 10 $
(D) $ x = 0 $ and $ y = x + 10 $

▶️ Answer/Explanation

Detailed solution

Factor denominator: $ x^2 + 2x = x(x+2) $. Zeros of denominator: $ x = 0 $ and $ x = -2 $.
Numerator zeros: $ x = -1, -2, -5 $.
Cancel $ x+2 $ (common factor) → hole at $ x = -2 $, not a vertical asymptote.
Vertical asymptote only at $ x = 0 $.
Degree numerator (after cancel) = 2, degree denominator = 1 ⇒ slant asymptote.
Perform division: $ \frac{x^2 + 7x + 5}{x} = x + 7 + \frac{5}{x} $ or redo original before cancel: Divide $ x^3 + 8x^2 + 17x + 10 $ by $ x^2 + 2x $ → quotient $ x + 6 $, remainder $ 5x + 10 $.
Thus slant asymptote: $ y = x + 6 $.
✅ Answer: (A)

Question

The function $ f $ is given by $ f(x) = -2x^7 + 5x^4 + 6x^2 – 3 $. Which of the following correctly describes the end behavior of $ f $ as the input values increase without bound?

(A) $ \lim_{x \to \infty} f(x) = \infty $
(B) $ \lim_{x \to \infty} f(x) = -\infty $
(C) $ \lim_{x \to -\infty} f(x) = \infty $
(D) $ \lim_{x \to -\infty} f(x) = -\infty $

▶️ Answer/Explanation

Detailed solution

Leading term: $ -2x^7 $, degree 7 (odd), coefficient negative.
For odd degree with negative leading coefficient:
As $ x \to \infty $, $ f(x) \to -\infty $.
As $ x \to -\infty $, $ f(x) \to \infty $.
The question asks for behavior as $ x \to \infty $.
✅ Answer: (B)

Question

The function $ f $ is given by $ f(x) = 5x^6 – 2x^3 – 3 $. Which of the following describes the end behavior of $ f $?

(A) $ \lim_{x \to -\infty} f(x) = -\infty $ and $ \lim_{x \to \infty} f(x) = -\infty $
(B) $ \lim_{x \to -\infty} f(x) = \infty $ and $ \lim_{x \to \infty} f(x) = \infty $
(C) $ \lim_{x \to -\infty} f(x) = -\infty $ and $ \lim_{x \to \infty} f(x) = \infty $
(D) $ \lim_{x \to -\infty} f(x) = \infty $ and $ \lim_{x \to \infty} f(x) = -\infty $

▶️ Answer/Explanation

Detailed solution

Leading term: $ 5x^6 $, degree 6 (even), coefficient positive.
For even degree with positive leading coefficient:
$ \lim_{x \to \pm\infty} f(x) = \infty $.
✅ Answer: (B)

Question

The rational function $ f $ is given by $ f(x) = \frac{x^k(x-1)(x+3)}{x^5+2x-5} $, where $ k $ is a positive integer. For which of the following values of $ k $ will the graph of $ f $ have a horizontal asymptote at $ y = 0 $?

(A) 2
(B) 3
(C) 4
(D) 5

▶️ Answer/Explanation

Detailed solution

The numerator is $ x^k(x-1)(x+3) $.
The degree of the numerator = $ k + 1 + 1 = k+2 $.
The denominator $ x^5 + 2x – 5 $ has degree $ 5 $.
Horizontal asymptote at $ y = 0 $ occurs when degree of denominator > degree of numerator.
So $ 5 > k+2 $ ⇒ $ k < 3 $.
Given $ k $ positive integer: possible $ k = 1 $ or $ 2 $.
Among choices, only $ k = 2 $ satisfies.
✅ Answer: (A) 2

Question

The rational function $ r $ is given by $ r(x) = \frac{(2x-3)(x-4)(x-2)}{(3x-1)(2x+1)(x-1)} $ and is equivalent to $ r(x) = \frac{p(x)}{q(x)} $, where $ p $ and $ q $ are polynomial functions. Which of the following statements is true?

(A) The degree of $ p $ is less than the degree of $ q $, and $ \lim_{x \to \infty} r(x) = 0 $.
(B) The degree of $ p $ is greater than the degree of $ q $, and $ \lim_{x \to \infty} r(x) = \infty $.
(C) The degree of $ p $ is equal to the degree of $ q $, and $ \lim_{x \to \infty} r(x) = 0 $.
(D) The degree of $ p $ is equal to the degree of $ q $, and $ \lim_{x \to \infty} r(x) = \frac{1}{3} $.

▶️ Answer/Explanation

Detailed solution

Numerator $ p(x) = (2x-3)(x-4)(x-2) $:
Leading term: $ 2x \cdot x \cdot x = 2x^3 $, degree 3.
Denominator $ q(x) = (3x-1)(2x+1)(x-1) $:
Leading term: $ 3x \cdot 2x \cdot x = 6x^3 $, degree 3.
Thus degree of $ p $ = degree of $ q $ = 3.
For large $ x $, $ r(x) \approx \frac{2x^3}{6x^3} = \frac{1}{3} $.
So $ \lim_{x \to \infty} r(x) = \frac{1}{3} $.
✅ Answer: (D)

Question

The rational function $ h $ is expressed as the quotient of two polynomial functions $ f $ and $ g $ by $ h(x) = \frac{f(x)}{g(x)} $. The function $ f $ is given by $ f(x) = 6x^3 – x^2 + 60x – 25 $. If the graph of $ h $ has a slant asymptote of $ y = 2x – 1 $, which of the following describes $ g $?

(A) $ g $ has degree 2 with leading coefficient 3.
(B) $ g $ has degree 2 with leading coefficient 12.
(C) $ g $ has degree 3 with leading coefficient 3.
(D) $ g $ has degree 4 with leading coefficient 12.

▶️ Answer/Explanation

Detailed solution

A rational function has a slant (oblique) asymptote when the degree of the numerator is exactly one more than the degree of the denominator.
Given $ f $ is degree 3, so $ g $ must be degree 2.
Slant asymptote $ y = 2x – 1 $ is the quotient from polynomial long division.
Leading term of $ f $ is $ 6x^3 $, leading term of $ g $ is $ ax^2 $.
$ \frac{6x^3}{ax^2} = \frac{6}{a}x $, which equals $ 2x $ (from $ 2x – 1 $).
So $ \frac{6}{a} = 2 $ ⇒ $ a = 3 $.
Thus $ g $ has degree 2, leading coefficient 3.
✅ Answer: (A)

Question

The rational function $ h $ is given by $ h(x) = \frac{2x^5 + 5x^3 – 2x^2 – 13}{3x^2 – 2x + 7} $. Which of the following describes the end behavior of $ h $?

(A) As $ x $ increases without bound, $ h(x) $ increases without bound, and as $ x $ decreases without bound, $ h(x) $ decreases without bound.
(B) As $ x $ increases without bound, $ h(x) $ increases without bound, and as $ x $ decreases without bound, $ h(x) $ increases without bound.
(C) As $ x $ increases without bound, $ h(x) $ decreases without bound, and as $ x $ decreases without bound, $ h(x) $ increases without bound.
(D) As $ x $ increases without bound, $ h(x) $ decreases without bound, and as $ x $ decreases without bound, $ h(x) $ decreases without bound.

▶️ Answer/Explanation

Detailed solution

Degree of numerator: 5, degree of denominator: 2.
Since numerator degree > denominator degree, no horizontal asymptote; end behavior ≈ $ \frac{2x^5}{3x^2} = \frac{2}{3}x^3 $.
Cubic $ \frac{2}{3}x^3 $ has positive leading coefficient.
For large positive $ x $, $ x^3 $ → +∞ ⇒ $ h(x) $ → +∞.
For large negative $ x $, $ x^3 $ → −∞ ⇒ $ h(x) $ → −∞.
Thus: as $ x \to +\infty $, $ h(x) \to +\infty $; as $ x \to -\infty $, $ h(x) \to -\infty $.
✅ Answer: (A)

Question

A polynomial function $ p $ has three distinct zeros each with multiplicity 1, and its leading coefficient is positive. The polynomial function $ q $ has exactly one zero with multiplicity 3, and its leading coefficient is negative. The rational function $ h $ can be written as the quotient of $ p $ and $ q $ by $ h(x) = \frac{p(x)}{q(x)} $. Which of the following statements about $ h $ must be true?

(A) The graph of $ h $ has a horizontal asymptote at $ y = 0 $.
(B) The graph of $ h $ has a horizontal asymptote at $ y = a $, where $ a > 0 $.
(C) The graph of $ h $ has a horizontal asymptote at $ y = a $, where $ a < 0 $.
(D) The graph of $ h $ has no horizontal asymptote.

▶️ Answer/Explanation

Detailed solution

$ p $ has three distinct zeros, each multiplicity 1 ⇒ degree $ p $ = 3, leading coefficient positive.
$ q $ has exactly one zero with multiplicity 3 ⇒ degree $ q $ = 3, leading coefficient negative.
Thus degree of numerator = degree of denominator = 3.
Horizontal asymptote exists at $ y = \frac{\text{leading coefficient of } p}{\text{leading coefficient of } q} $.
Let leading coefficient of $ p $ be $ A > 0 $, of $ q $ be $ B < 0 $.
Then $ a = \frac{A}{B} < 0 $.
So horizontal asymptote is $ y = a $ where $ a < 0 $.
✅ Answer: (C)

Question

The rational function $f(x) = \frac{-x^8 + 3x + 5}{-x^7 + 2x^8 + 3x – 2}$. Which limit is correct based on the function’s horizontal asymptote?

a. $\lim_{x \to -\infty} f(x) = 1/2$

b. $\lim_{x \to -\infty} f(x) = -1/2$

c. $\lim_{x \to -\infty} f(x) = 0$

d. $\lim_{x \to -\infty} f(x) = \infty$

▶️ Answer/Explanation

Detailed solution

Identify the leading terms in the numerator and denominator.
The numerator’s leading term is $-x^8$ and the denominator’s is $2x^8$.
Since the degrees are equal ($8 = 8$), the horizontal asymptote is the ratio of leading coefficients.
The limit as $x \to -\infty$ is determined by $\frac{-1}{2}$.
Therefore, $\lim_{x \to -\infty} f(x) = -1/2$.
This matches option b.

Question

If $f(x) = \frac{p(x)}{q(x)}$ where $p(x)$ is a quadratic and $q(x)$ is a cubic function with their graphs shown above, then which of the following limits is true for $f(x)$?

a. $\lim_{x \to -\frac{5}{2}^-} f(x) = -\infty$

b. $\lim_{x \to \infty} f(x) = -\frac{1}{4}$

c. $\lim_{x \to 5^+} f(x) = \infty$

d. $\lim_{x \to -\frac{5}{2}^+} f(x) = \infty$

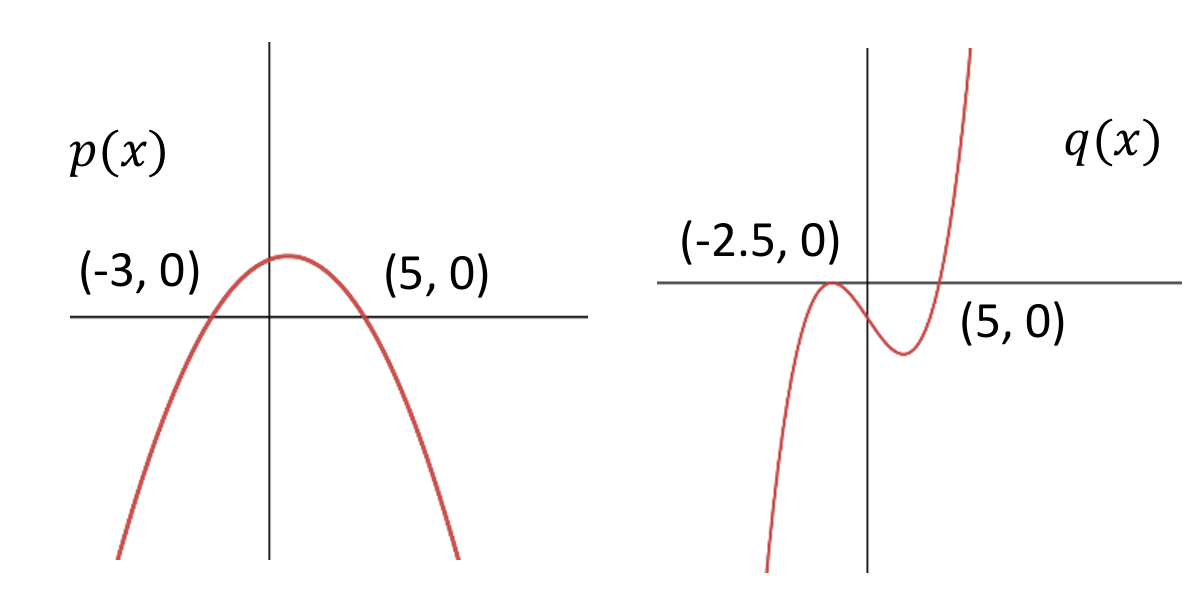
▶️ Answer/Explanation

Detailed solution

From the graphs, $p(x)$ has roots at $x = -3$ and $x = 5$, so $p(x) = a(x + 3)(x – 5)$ with $a < 0$.
The graph of $q(x)$ shows a bounce at $x = -2.5$ and a cross at $x = 5$, so $q(x) = b(x + 2.5)^2(x – 5)$ with $b > 0$.
The function $f(x) = \frac{a(x + 3)(x – 5)}{b(x + 2.5)^2(x – 5)} = \frac{a(x + 3)}{b(x + 2.5)^2}$ for $x \neq 5$.
At $x = -2.5$, the denominator $(x + 2.5)^2$ is always positive as $x \to -2.5$ from either side.
The numerator $a(x + 3)$ is negative because $a < 0$ and $(-2.5 + 3) = 0.5 > 0$.
Thus, $f(x) \to \frac{\text{negative}}{\text{positive } \to 0} = -\infty$ as $x \to -2.5$.
Therefore, $\lim_{x \to -\frac{5}{2}^-} f(x) = -\infty$ is correct.
Correct Option: a

Question

Let $f$ and $g$ be polynomials such that $f(x) = x^2 – 6x + 7$ and $g(x) = x – 2$. If $h$ is a rational function given by $h(x) = \frac{f(x)}{g(x)}$, which of the following is the slant asymptote to the graph $h(x)$?

(A) $y = x – 8$

(B) $y = x – 4$

(D) $y = x + 4$

▶️ Answer/Explanation

Detailed solution

The correct option is (B).

To find the slant asymptote, we divide the numerator by the denominator:
1. We represent the function as $h(x) = \frac{x^2 – 6x + 7}{x – 2}$.
2. Perform polynomial long division: Divide $x^2$ by $x$ to get $x$. Multiply $x(x – 2) = x^2 – 2x$.
3. Subtract $(x^2 – 6x) – (x^2 – 2x)$ to result in $-4x$. Bring down the $+7$.
4. Divide $-4x$ by $x$ to get $-4$. Multiply $-4(x – 2) = -4x + 8$.
5. Subtract $(-4x + 7) – (-4x + 8)$ to get a remainder of $-1$.
6. The function can be written as $h(x) = (x – 4) – \frac{1}{x – 2}$.
7. As $x \rightarrow \infty$, the remainder fraction approaches 0, leaving the slant asymptote $y = x – 4$.

Question

$$f(x) = \frac{x^2 – 4}{x^2 – 2x + 2}$$

The graph of $ y = f(x) $ will cross its horizontal asymptote at $ (a, b) $. What is the value of $ a + b $?

(A) $ 3\sqrt{3} $
(B) $ 7 $
(C) $ 4 $
(D) $ \frac{5}{3} $

▶️ Answer/Explanation

Detailed solution

To find the horizontal asymptote, compare the degrees of the numerator and denominator; since both are 2, the asymptote is $ y = \frac{1}{1} = 1 $, so $ b = 1 $.
Set the function equal to the asymptote to find the intersection: $ \frac{x^2 – 4}{x^2 – 2x + 2} = 1 $.
Multiply across and simplify: $ x^2 – 4 = x^2 – 2x + 2 $.
Subtract $ x^2 $ from both sides to get $ -4 = -2x + 2 $.
Solve for $ x $: $ 2x = 6 \Rightarrow x = 3 $, so $ a = 3 $.
Finally, calculate the sum: $ a + b = 3 + 1 = 4 $.
Therefore, the correct option is (C).

Question

The rational function $f$ is given by $f(x) = \frac{x^3 – x^2 – 4x}{x^2 – 4x}$. In the $xy$-plane, which of the following is the slope of a slant asymptote of the graph of $f$?

(A) $0$

(B) $1$

(D) $8$

▶️ Answer/Explanation

Detailed solution

The correct option is (B).

First, simplify the function by factoring out $x$ from both the numerator and denominator: $f(x) = \frac{x(x^2 – x – 4)}{x(x – 4)}$.
Cancel the common factor $x$ (for $x \neq 0$) to get the simplified form: $f(x) = \frac{x^2 – x – 4}{x – 4}$.
To find the slant asymptote, perform polynomial long division of the numerator $(x^2 – x – 4)$ by the denominator $(x – 4)$.
Divide the leading term $x^2$ by $x$ to get the first term of the quotient, which is $x$.
Multiply $x(x – 4) = x^2 – 4x$ and subtract from the numerator: $(x^2 – x) – (x^2 – 4x) = 3x$.
Divide the remaining $3x$ by $x$ to get the second term of the quotient, which is $+3$.
The quotient represents the slant asymptote: $y = x + 3$.
The equation is in the form $y = mx + c$, so the slope $m$ is $1$.

Question

The function $f$ is given by $f(x) = \frac{x^2 – 9}{(x+3)(x^2 + 2x – 15)}$. Which of the following is true about the graph of $f$ in the $xy$-plane?

A. The graph of $f$ has no vertical asymptotes, and there are exactly two holes in the graph of $f$, one at $x = -3$ and one at $x = 3$.

B. The graph of $f$ has a vertical asymptote at $x = -5$ only, and there are exactly two holes in the graph of $f$, one at $x = -3$ and one at $x = 3$.

C. The graph of $f$ has vertical asymptotes at $x = -3$ and $x = 3$ only, and there is exactly one hole in the graph of $f$ at $x = -5$.

D. The graph of $f$ has vertical asymptotes at $x = -5$, $x = -3$, and $x = 3$, and there are no holes in the graph of $f$.

▶️ Answer/Explanation

Detailed solution

First, factor the numerator completely: $x^2 – 9 = (x-3)(x+3)$.

Next, factor the quadratic expression in the denominator: $(x^2 + 2x – 15) = (x+5)(x-3)$.

Substitute these back into the function: $f(x) = \frac{(x-3)(x+3)}{(x+3)(x+5)(x-3)}$.

Identify holes where factors cancel out: The terms $(x+3)$ and $(x-3)$ appear in both numerator and denominator, causing holes at $x = -3$ and $x = 3$.

Identify vertical asymptotes where factors remain in the denominator: The term $(x+5)$ remains, causing a vertical asymptote at $x = -5$.

Therefore, the graph has a vertical asymptote at $x = -5$ only, and holes at $x = -3$ and $x = 3$.

Correct Option: B

Question

Let $f$ and $g$ be polynomials such that $f(x) = -2x^2 + 3x – 8$ and $g(x) = x + 3$. If $h$ is a rational function given by $h(x) = \frac{f(x)}{g(x)}$, which of the following is the slant asymptote to the graph $h(x)$?

(A) $y = -2x – 3$
(B) $y = -2x + 1$
(C) $y = -2x + 9$
(D) $y = 2x + 9$

▶️ Answer/Explanation

Detailed solution

To find the slant asymptote, divide $f(x) = -2x^2 + 3x – 8$ by $g(x) = x + 3$.
Using synthetic division with the root $x = -3$:
The coefficients are $-2$, $3$, and $-8$.
Bring down $-2$, then multiply $-3 \times -2 = 6$.
Add $3 + 6 = 9$ to get the second coefficient of the quotient.
The resulting quotient is $-2x + 9$.
As $x \to \infty$, the remainder term $\frac{-35}{x+3}$ approaches $0$.
Thus, the equation of the slant asymptote is $y = -2x + 9$.
The correct option is (C).

Question

The rational function is given by $ r(x) = \dfrac{x^3 + 8x^2 + 17x + 10}{x^2 + 2x} = \dfrac{(x+1)(x+2)(x+5)}{x(x+2)} $. Which of the following gives the equations for all the horizontal, vertical, and slant asymptotes?

(A) $ x = 0 $ and $ y = x + 6 $

(B) $ x = 0 $ and $ x = -2 $

(C) $ x = 0 $ and $ y = 5x + 10 $

(D) $ x = 0 $ and $ y = x + 10 $

▶️ Answer/Explanation

Correct Answer: (A)

Detailed Solution

1. Factor the function: $ r(x) = \dfrac{(x+1)(x+2)(x+5)}{x(x+2)} $.

2. Cancel $ (x+2) $ (note $ x \ne -2 $), giving $ r(x) = \dfrac{(x+1)(x+5)}{x} $.

3. Expand numerator: $ r(x) = \dfrac{x^2 + 6x + 5}{x} $.

4. Divide: $ r(x) = x + 6 + \dfrac{5}{x} $.

5. Vertical asymptote occurs where denominator = 0 → $ x = 0 $.

6. Since degree(numerator) = degree(denominator) + 1, slant asymptote is $ y = x + 6 $.

7. No horizontal asymptote exists.

Therefore, the correct answer is (A).

Question

The rational function is given by $ f(x) = \dfrac{x^{k}(x-1)(x+3)}{x^{5}+2x-5} $, where $ k $ is a positive integer.

For which value of $ k $ will the graph of $ f $ have a horizontal asymptote at $ y = 0 $?

(A) $ 2 $

(B) $ 3 $

(D) $ 5 $

▶️ Answer/Explanation

Answer:

(A) $ 2 $

Explanation:

A rational function has a horizontal asymptote at $ y = 0 $ when the degree of the numerator is strictly less than the degree of the denominator.

The numerator has degree $ k + 2 $ and the denominator has degree $ 5 $.

For a horizontal asymptote at $ y = 0 $, we require $ k + 2 < 5 $, which gives $ k < 3 $.

Since $ k $ is a positive integer and the given options are $ 2,3,4,5 $, the only possible value is $ k = 2 $.

Detailed solution

1. Degree of numerator $ = k + 2 $ because $ x^{k}(x-1)(x+3) $ expands to highest power $ x^{k+2} $.
2. Degree of denominator $ = 5 $ since highest power in $ x^{5}+2x-5 $ is $ 5 $.
3. Horizontal asymptote $ y = 0 $ occurs when numerator degree $ < $ denominator degree.
4. Thus $ k + 2 < 5 $.
5. Solving gives $ k < 3 $.
6. Since $ k $ is a positive integer, possible values are $ 1,2 $.
7. From the given options, only $ k = 2 $ satisfies the condition.
8. Therefore, the correct answer is $ \boxed{2} $.

Question

(A) The degree of $ p $ is less than the degree of $ q $, and $ \displaystyle \lim_{x\to\infty} r(x) = 0 $.

(B) The degree of $ p $ is greater than the degree of $ q $, and $ \displaystyle \lim_{x\to\infty} r(x) = \infty $.

(D) The degree of $ p $ is equal to the degree of $ q $, and $ \displaystyle \lim_{x\to\infty} r(x) = \frac{1}{3} $.

▶️ Answer/Explanation

Detailed solution

To find the degree of the numerator $ p(x) $, we multiply the leading terms of its factors: $ (2x)(x)(x) = 2x^3 $, so the degree is 3.
To find the degree of the denominator $ q(x) $, we multiply the leading terms of its factors: $ (3x)(2x)(x) = 6x^3 $, so the degree is 3.
Comparing the two, the degree of $ p $ is equal to the degree of $ q $.
Since the degrees are equal, the horizontal asymptote (limit as $ x \to \infty $) is the ratio of the leading coefficients.
The limit is calculated as $ \displaystyle \lim_{x\to\infty} r(x) = \frac{2}{6} = \frac{1}{3} $.
Therefore, statement (D) corresponds to these findings.

Question

The function $ h $ is given by $ h(x) = \frac{2x^3}{x+3} – \frac{4}{x-1}. $ Which of the following statements is true?

(A) $ h $ is equivalent to $ \frac{2x^4 – 2x^3 – 4x – 12}{x^2 + 2x – 3} $ and has the same end behavior as the graph of $ y = 2x^2 $.

(B) $ h $ is equivalent to $ \frac{2x^3 – 4}{x^2 + 2x – 3} $ and has the same end behavior as the graph of $ y = 2x $.

(C) $ h $ is equivalent to $ \frac{2x^3}{x} + \frac{2x^3}{3} – \frac{4}{x-1} $ and has the same end behavior as the graph of $ y = 2x^2 $.

(D) $ h $ is equivalent to $ \frac{2x^2 – 2x – 12}{3x – 3} $ and has the same end behavior as the graph of $ y = 2x $.

▶️ Answer/Explanation

Answer: (A)

Detailed solution

1. The common denominator of $ \frac{2x^3}{x+3} $ and $ \frac{4}{x-1} $ is $ (x+3)(x-1) = x^2 + 2x – 3 $.
2. Rewrite: $ \frac{2x^3}{x+3} = \frac{2x^3(x-1)}{(x+3)(x-1)} = \frac{2x^4 – 2x^3}{x^2+2x-3} $.
3. Rewrite: $ \frac{4}{x-1} = \frac{4(x+3)}{(x+3)(x-1)} = \frac{4x + 12}{x^2+2x-3} $.
4. Subtract numerators: $ 2x^4 – 2x^3 – (4x+12) $.
5. Thus $ h(x) = \frac{2x^4 – 2x^3 – 4x – 12}{x^2+2x-3} $.
6. For end behavior, compare leading terms: $ \frac{2x^4}{x^2} = 2x^2 $.
7. Therefore, $ h(x) $ has the same end behavior as $ y = 2x^2 $.
8. Hence, option (A) is correct.

Question

The rational function $ h $ is expressed as the quotient of two polynomial functions $ f $ and $ g $ by $ h(x)=\frac{f(x)}{g(x)}. $ The function $ f $ is given by $ f(x)=6x^3 – x^2 + 60x – 25. $ If the graph of $ h $ has a slant asymptote of $ y = 2x – 1, $ which of the following describes $ g $?

(A) $ g $ has degree $2$ with leading coefficient $3$.

(B) $ g $ has degree $2$ with leading coefficient $12$.

(D) $ g $ has degree $4$ with leading coefficient $12$.

▶️ Answer/Explanation

Answer:

(A) $ g $ has degree $2$ with leading coefficient $3$.

Explanation:

A slant (oblique) asymptote occurs when the degree of the numerator is exactly one greater than the degree of the denominator. Since $ \deg f = 3 $, we must have $ \deg g = 2 $. The slant asymptote equals the quotient obtained from polynomial division. Comparing leading terms: \[ \frac{6x^3}{ax^2} = \frac{6}{a}x. \] Given the asymptote is $2x – 1$, we require \[ \frac{6}{a} = 2 \Rightarrow a = 3. \] Thus $ g $ has degree $2$ with leading coefficient $3$.

Detailed solution

1. Since $ \deg f = 3 $ and a slant asymptote exists, $ \deg g = 2 $.
2. Let the leading term of $ g(x) $ be $ ax^2 $.
3. The leading term of the quotient is $ \dfrac{6x^3}{ax^2} = \dfrac{6}{a}x $.
4. The slant asymptote is $ 2x – 1 $, so $ \dfrac{6}{a} = 2 $.
5. Solving gives $ a = 3 $.
6. Therefore, $ g $ is degree $2$ with leading coefficient $3$.

Question

The rational function $ h $ is given by $ h(x)=\frac{2x^{5}+5x^{3}-2x^{2}-13}{3x^{2}-2x+7}. $ Which of the following describes the end behavior of $ h $?

(A) As $x \to +\infty$, $h(x) \to +\infty$, and as $x \to -\infty$, $h(x) \to -\infty$.

(B) As $x \to +\infty$, $h(x) \to +\infty$, and as $x \to -\infty$, $h(x) \to +\infty$.

(D) As $x \to +\infty$, $h(x) \to -\infty$, and as $x \to -\infty$, $h(x) \to -\infty$.

▶️ Answer/Explanation

Answer:

(A)

Explanation:

To determine end behavior, compare the highest-degree terms in the numerator and denominator.

The leading term of the numerator is $2x^{5}$ and the leading term of the denominator is $3x^{2}$.

Thus, for large $|x|$, \[ h(x) \sim \frac{2x^{5}}{3x^{2}} = \frac{2}{3}x^{3}. \]

Since $\frac{2}{3}x^{3}$ is a cubic with positive leading coefficient:

As $x \to +\infty$, $h(x) \to +\infty$.

As $x \to -\infty$, $h(x) \to -\infty$.

Detailed solution

1. Highest power in numerator: $2x^{5}$.
2. Highest power in denominator: $3x^{2}$.
3. Dominant behavior: $\frac{2x^{5}}{3x^{2}}=\frac{2}{3}x^{3}$.
4. Degree difference $=5-2=3$, so behavior is cubic.
5. Leading coefficient $\frac{2}{3} > 0$.
6. Therefore $h(x)\to +\infty$ as $x\to +\infty$.
7. And $h(x)\to -\infty$ as $x\to -\infty$.

Question

A polynomial function $p$ has three distinct zeros each with multiplicity 1, and its leading coefficient is positive. The polynomial function $q$ has exactly one zero with multiplicity 3, and its leading coefficient is negative. The rational function $h$ can be written as the quotient of $p$ and $q$ by $h(x) = \frac{p(x)}{q(x)}$. Which of the following statements about $h$ must be true?

(A) The graph of $h$ has a horizontal asymptote at $y = 0$.

(B) The graph of $h$ has a horizontal asymptote at $y = a$, where $a > 0$.

(D) The graph of $h$ has no horizontal asymptote.

▶️ Answer/Explanation

Detailed solution

The degree of polynomial $p$ is determined by its zeros: 3 zeros $\times$ multiplicity 1 = degree 3.
The degree of polynomial $q$ is determined by its zeros: 1 zero $\times$ multiplicity 3 = degree 3.
For the rational function $h(x) = \frac{p(x)}{q(x)}$, the numerator and denominator have equal degrees.
Therefore, the horizontal asymptote is the ratio of the leading coefficients: $y = \frac{\text{leading coefficient of } p}{\text{leading coefficient of } q}$.
Since the leading coefficient of $p$ is positive and $q$ is negative, their ratio $a$ must be negative ($a < 0$).
Thus, the graph has a horizontal asymptote at $y = a$, where $a < 0$.
Correct Option: (C)

Question

The rational function $f$ is given by $ f(x) = \frac{x^3 – x^2 – 4x}{x^2 – 4x}. $ In the $xy$-plane, which of the following is the slope of a slant asymptote of the graph of $f$?

(A) 0

(B) 1

(D) 8

▶️ Answer/Explanation

Answer

Answer: (C) 3

Detailed solution

Step 1: Factor numerator and denominator: \[ f(x) = \frac{x(x^2 – x – 4)}{x(x-4)} = \frac{x^2 – x – 4}{x-4}, \quad x \neq 0. \]

Step 2: Perform polynomial long division of $x^2 – x – 4$ by $x – 4$: \[ x^2 – x – 4 \div (x-4) = x + 3 + \frac{8}{x-4}. \]

Step 3: As $x \to \infty$, the term $\frac{8}{x-4} \to 0$, so the slant asymptote is \[ y = x + 3. \]

Step 4: The slope of the slant asymptote is the coefficient of $x$: \[ m = 1. \]

Step 5: Double-check: Division confirms the slope is correct, and the asymptote is linear.

Note: The slope of the slant asymptote is determined only by the highest degree terms in the numerator and denominator, and matches the coefficient from the long division.

AP Precalculus -1.7 Rational Functions and End Behavior- MCQ Exam Style Questions - Effective Fall 2023