AP Precalculus -1.7 Rational Functions and End Behavior- Study Notes - Effective Fall 2023
AP Precalculus -1.7 Rational Functions and End Behavior- Study Notes – Effective Fall 2023
AP Precalculus -1.7 Rational Functions and End Behavior- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Describe end behaviors of rational functions.
Key Concepts:
- Rational Functions
- End Behavior of Rational Functions
- Slant Asymptotes and End Behavior of Rational Functions
- Horizontal Asymptotes of Rational Functions
- Horizontal Asymptote at y=0 for Rational Functions
- Meaning of a Horizontal Asymptote
Rational Functions
A rational function is a function that can be written as a quotient of two polynomial functions.![]()
Analytically, a rational function has the form
\( r(x) = \dfrac{p(x)}{q(x)} \)
where \( p(x) \) and \( q(x) \) are polynomial functions and \( q(x) \ne 0 \).
A rational function compares the relative size of the numerator polynomial to the denominator polynomial for each value of \( x \) in the function’s domain.
The domain of a rational function includes all real numbers except those that make the denominator equal to zero.
As the input values change, the output depends on how fast the numerator grows or shrinks compared to the denominator.
Example:
Consider the rational function \( r(x) = \dfrac{2x}{x + 1} \).
Identify the domain and explain how the function compares the numerator and denominator.
▶️ Answer/Explanation
Domain
The denominator cannot be zero.
\( x + 1 \ne 0 \Rightarrow x \ne -1 \)
Interpretation
For each value of \( x \), the function measures how the value of \( 2x \) compares to the value of \( x + 1 \).
As \( x \) becomes large, both numerator and denominator grow at similar rates.
Example:
The function \( f(x) = \dfrac{x^2 – 1}{x^2 + 3} \) is a rational function.
Describe what the function represents.
▶️ Answer/Explanation
Both the numerator and denominator are quadratic polynomials.
For each input value \( x \), the function compares the size of \( x^2 – 1 \) to the size of \( x^2 + 3 \).
Since both grow at similar rates for large \( |x| \), the output values approach a constant.
Conclusion
This rational function measures how one quadratic expression compares to another across its domain.
End Behavior of Rational Functions
The end behavior of a rational function describes how the output values behave as the input values have large magnitude, meaning as \( x \to \infty \) or \( x \to -\infty \).
For a rational function written as
\( r(x) = \dfrac{p(x)}{q(x)} \)
the end behavior is affected most by the polynomial with the greater degree.
As \( |x| \) becomes large, each polynomial is dominated by its leading term. All lower-degree terms become insignificant in comparison.
Therefore, the end behavior of a rational function can be understood by examining the quotient of the leading terms of the numerator and denominator.
Key Cases
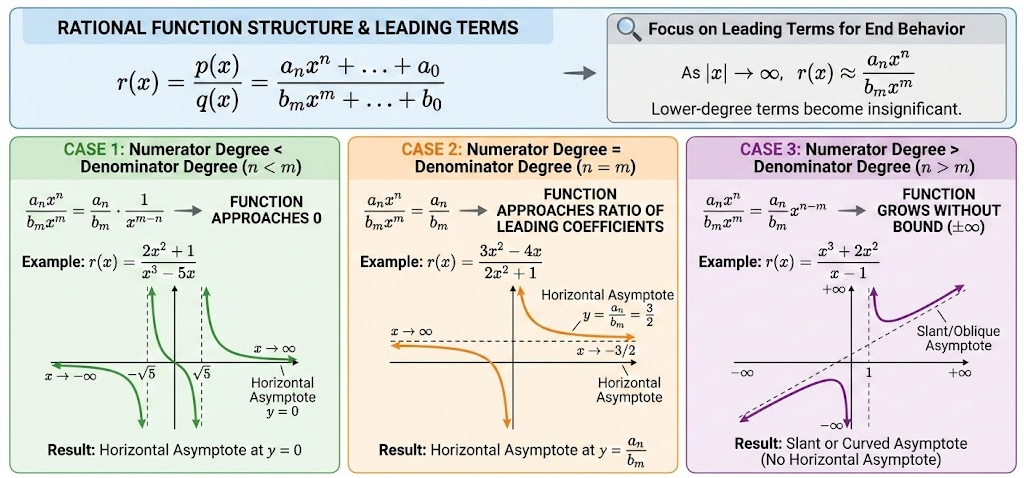
Let the leading terms be \( a_n x^n \) in the numerator and \( b_m x^m \) in the denominator.
If \( n < m \): the function approaches 0.
If \( n = m \): the function approaches \( \dfrac{a_n}{b_m} \).
If \( n > m \): the function grows without bound or decreases without bound.
Example:
Determine the end behavior of the rational function
\( r(x) = \dfrac{3x^2 + 5}{x^3 – 2} \)
▶️ Answer/Explanation
The leading term of the numerator is \( 3x^2 \).
The leading term of the denominator is \( x^3 \).
Since the degree of the numerator is less than the degree of the denominator, the denominator dominates.
Conclusion
As \( x \to \pm\infty \), \( r(x) \to 0 \).
Example:
Describe the end behavior of
\( f(x) = \dfrac{4x^3 – x}{2x^3 + 7} \)
▶️ Answer/Explanation
The leading terms are \( 4x^3 \) and \( 2x^3 \).
The quotient of the leading terms is
\( \dfrac{4x^3}{2x^3} = 2 \)
Conclusion
As \( x \to \pm\infty \), \( f(x) \to 2 \).
Slant Asymptotes and End Behavior of Rational Functions
Consider a rational function written as
\( r(x) = \dfrac{p(x)}{q(x)} \)
If the degree of the polynomial in the numerator is greater than the degree of the polynomial in the denominator, then the numerator dominates for input values of large magnitude.
In this case, the quotient of the leading terms is a nonconstant polynomial, and the rational function has the same end behavior as that polynomial.
This quotient can be found using polynomial division.
Slant (Oblique) Asymptotes
If the quotient of the leading terms is a linear polynomial, then the graph of the rational function has a slant asymptote.
A slant asymptote is a line that the graph approaches as \( x \to \pm\infty \).
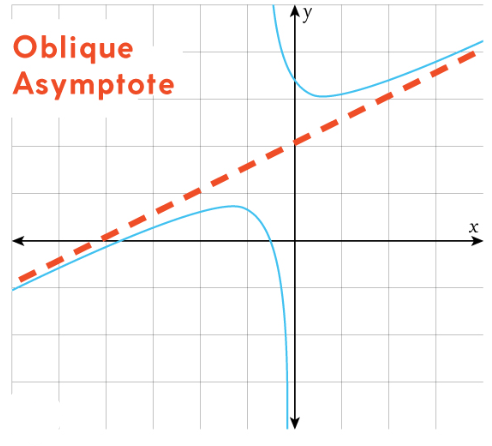
The slant asymptote is parallel to the graph of the linear polynomial obtained from the quotient.
Example:
Find the end behavior and slant asymptote of
\( r(x) = \dfrac{x^2 + 3x + 1}{x + 1} \)
▶️ Answer/Explanation
The degree of the numerator is greater than the degree of the denominator.
Divide the polynomials:
\( \dfrac{x^2 + 3x + 1}{x + 1} = x + 2 – \dfrac{1}{x + 1} \)
The quotient is the linear polynomial \( y = x + 2 \).
Conclusion
The rational function has the same end behavior as \( y = x + 2 \).
The graph has a slant asymptote \( y = x + 2 \).
Example:
Determine whether the rational function has a slant asymptote:
\( f(x) = \dfrac{2x^3 – x}{x^2 + 1} \)
▶️ Answer/Explanation
The degree of the numerator is one more than the degree of the denominator.
Perform polynomial division:
\( \dfrac{2x^3 – x}{x^2 + 1} = 2x – \dfrac{3x}{x^2 + 1} \)
The quotient is the linear polynomial \( y = 2x \).
Conclusion
The rational function has a slant asymptote \( y = 2x \).
Horizontal Asymptotes of Rational Functions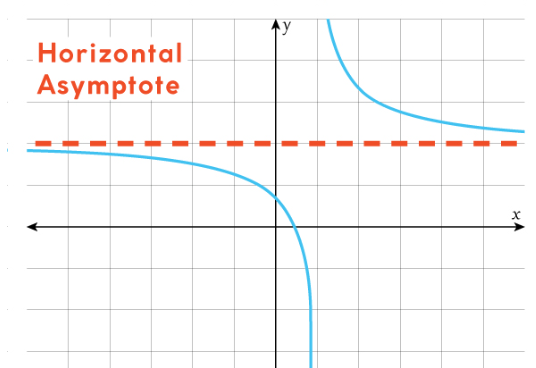
Consider a rational function written as
\( r(x) = \dfrac{p(x)}{q(x)} \)
If neither polynomial dominates the other for input values of large magnitude, then the degrees of the numerator and denominator are equal.
In this case, the end behavior of the rational function is determined by the quotient of the leading terms.
Since the degrees are the same, the quotient of the leading terms is a constant.
This constant gives the equation of a horizontal asymptote of the graph.
If the leading terms are \( a_n x^n \) and \( b_n x^n \), then
\( \text{Horizontal asymptote: } y = \dfrac{a_n}{b_n} \)
The graph of the rational function approaches this horizontal line as \( x \to \pm\infty \).
Example:
Find the horizontal asymptote of the rational function
\( f(x) = \dfrac{3x^2 + 5x – 1}{2x^2 – 7} \)
▶️ Answer/Explanation
The degree of the numerator and denominator is 2.
The leading terms are \( 3x^2 \) and \( 2x^2 \).
Compute the quotient of the leading coefficients:
\( \dfrac{3}{2} \)
Conclusion
The horizontal asymptote is \( y = \dfrac{3}{2} \).
Example:
Describe the end behavior and horizontal asymptote of
\( r(x) = \dfrac{-5x^3 + 2}{10x^3 – x} \)
▶️ Answer/Explanation
Both the numerator and denominator have degree 3.
The leading terms are \( -5x^3 \) and \( 10x^3 \).
Compute the quotient of the leading coefficients:
\( \dfrac{-5}{10} = -\dfrac{1}{2} \)
Conclusion
The rational function has a horizontal asymptote at \( y = -\dfrac{1}{2} \).
As \( x \to \pm\infty \), the graph approaches this horizontal line.
Horizontal Asymptote at \( y = 0 \) for Rational Functions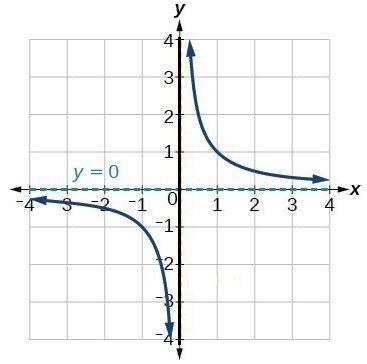
Consider a rational function written as
\( r(x) = \dfrac{p(x)}{q(x)} \)
If the degree of the polynomial in the denominator is greater than the degree of the polynomial in the numerator, then the denominator dominates for input values of large magnitude.
As \( |x| \) becomes large, both polynomials are dominated by their leading terms.
In this case, the quotient of the leading terms becomes a rational expression with a constant numerator and a nonconstant polynomial denominator.
As a result, the value of the rational function approaches 0.
Therefore, the graph of the rational function has a horizontal asymptote at
\( y = 0 \)
This means the graph gets closer and closer to the x-axis as \( x \to \pm\infty \), but does not necessarily touch it.
Example:
Find the horizontal asymptote of the rational function
\( f(x) = \dfrac{5x + 1}{x^2 + 3} \)
▶️ Answer/Explanation
The degree of the numerator is 1.
The degree of the denominator is 2.
Since the denominator has greater degree, it dominates for large \( |x| \).
Conclusion
The horizontal asymptote is \( y = 0 \).
Example:
Describe the end behavior of
\( r(x) = \dfrac{2x^2 – 7}{x^5 + 4} \)
▶️ Answer/Explanation
The numerator has degree 2 and the denominator has degree 5.
For large \( |x| \), the denominator grows much faster than the numerator.
Therefore, the value of the rational function approaches 0.
Conclusion
The graph has a horizontal asymptote at \( y = 0 \).
Meaning of a Horizontal Asymptote
Let \( r(x) \) be a rational function.
If the graph of \( r(x) \) has a horizontal asymptote at \( y = b \), where \( b \) is a constant, then the output values of the function approach \( b \) as the input values increase or decrease without bound.

This means that for very large positive or negative values of \( x \), the values of \( r(x) \) get arbitrarily close to \( b \) and remain close.
Mathematically, this behavior is described using limits:
\( \lim_{x \to \infty} r(x) = b \)
or
\( \lim_{x \to -\infty} r(x) = b \)
A horizontal asymptote describes the end behavior of a rational function. The graph may cross the asymptote, but it will approach the asymptote as \( x \to \pm\infty \).
Example:
Consider the rational function
\( r(x) = \dfrac{2x + 1}{x + 3} \)
Describe the meaning of its horizontal asymptote.
▶️ Answer/Explanation
The degrees of the numerator and denominator are equal.
The leading coefficients are 2 and 1.
So the horizontal asymptote is
\( y = 2 \)
Interpretation
As \( x \to \infty \) or \( x \to -\infty \), the values of \( r(x) \) get closer and closer to 2 and remain close to 2.
Example:
A rational function satisfies
\( \lim_{x \to \infty} r(x) = -3 \)
Explain what this statement means in terms of the graph.
▶️ Answer/Explanation
The graph has a horizontal asymptote at
\( y = -3 \)
As the input values become very large, the output values of the function approach −3.
The graph gets arbitrarily close to the line \( y = -3 \) and stays close for large values of \( x \).
