AP Precalculus -1.8 Rational Functions and Zeros- MCQ Exam Style Questions - Effective Fall 2023
AP Precalculus -1.8 Rational Functions and Zeros- MCQ Exam Style Questions – Effective Fall 2023
AP Precalculus -1.8 Rational Functions and Zeros- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.
▶️ Answer/Explanation
Degree of \( g \) is 2, degree of \( f \) is 4. After division, quotient degree = 2, remainder degree < 2.
Given answer says remainder is \( 7x – 5 \). Then \( g(x) \) is not a factor. Slant asymptote occurs when degree of numerator is exactly one more than degree of denominator. Here degree of \( f \) is 4, degree of \( g \) is 2 ⇒ degree difference = 2 ⇒ quotient is quadratic, not linear ⇒ no slant asymptote.
✅ Answer: (D)
▶️ Answer/Explanation
Factor \( g(x) \) and \( h(x) \):
\( g(x) = x^3 – 3x^2 – 18x = x(x^2 – 3x – 18) = x(x – 6)(x + 3) \)
Zeros of \( g \): \( x = 0, 6, -3 \)
\( h(x) = x^2 – 2x – 35 = (x – 7)(x + 5) \)
Thus \( k(x) = \frac{(x-7)(x+5)}{x(x-6)(x+3)} \)
Domain excludes zeros of denominator unless canceled by numerator. None of the numerator factors cancel with denominator factors.
So domain: all real \( x \) except \( x = 0, 6, -3 \).
✅ Answer: (C)
▶️ Answer/Explanation
Zeros of \( g \) occur where numerator = 0 and denominator ≠ 0.
Numerator: \( (x^2+3x)(x^2-4x-5) = x(x+3)(x-5)(x+1) \).
Zeros: \( x = 0, -3, 5, -1 \).
Denominator zeros: \( x = -3, 1, 2 \) (excluded from domain).
Thus zero \( x = -3 \) is not in domain (makes denominator zero).
So valid zeros: \( -1, 0, 5 \).
✅ Answer: (B)
▶️ Answer/Explanation
Factor: \( r(x) = \frac{x(x^2+4x+4)}{x^2-9} = \frac{x(x+2)^2}{(x-3)(x+3)} \).
Zeros of numerator: \( x = 0 \) (odd multiplicity 1), \( x = -2 \) (even multiplicity 2).
Vertical asymptotes at \( x = 3, -3 \).
Sign chart with test points in intervals:
\( (-\infty, -3) \): test \( x=-4 \) ⇒ \( r(-4) = (-)(+)/(-)(-) = (+)/(-) = (-) \) ⇒ negative.
\( (-3, -2) \): test \( x=-2.5 \) ⇒ \( (-)(+)/(-)(+) = (-)/(-) = (+) \) ⇒ positive, include \( x=-2 \) because zero but multiplicity even doesn’t change sign, check \( r(-2)=0 \) ⇒ include.
\( (-2, 0) \): test \( x=-1 \) ⇒ \( (-)(+)/(-)(+) = (-)/(-) = (+) \) ⇒ positive.
\( (0, 3) \): test \( x=1 \) ⇒ \( (+)(+)/(-)(+) = (+)/(-) = (-) \) ⇒ negative.
\( (3, \infty) \): test \( x=4 \) ⇒ \( (+)(+)/(+)(+) = (+) \) ⇒ positive.
We need \( r(x) \geq 0 \), so include zeros \( x=0, x=-2 \) and positive intervals.
Thus solution: \( -3 < x \leq 0 \) (since zero at 0, zero at -2 included, and -3 not included due to VA) and \( x > 3 \).
✅ Answer: (D)
▶️ Answer/Explanation
Zeros: \( x = -2, 0, 4 \).
Leading term: \( -x \cdot x \cdot x = -x^3 \), so as \( x \to -\infty \), \( p(x) \to +\infty \) (since \(-(\text{negative}) = \text{positive}\)).
Sign analysis:
Intervals: \( (-\infty, -2), (-2, 0), (0, 4), (4, \infty) \).
Test values:
\( x = -3 \): \( p(-3) = -(-3)(-7)(-1) = -(\text{negative})(\text{negative})(\text{negative}) = -(\text{negative}) = \text{positive} \) ⇒ \( + \).
\( x = -1 \): \( -(-1)(-5)(1) = -(\text{negative})(\text{negative})(\text{positive}) = -(\text{positive}) = \text{negative} \) ⇒ \( – \).
\( x = 1 \): \( -(1)(-3)(3) = -(\text{positive})(\text{negative})(\text{positive}) = -(\text{negative}) = \text{positive} \) ⇒ \( + \).
\( x = 5 \): \( -(5)(1)(7) = \text{negative} \) ⇒ \( – \).
We want \( p(x) \geq 0 \): intervals where sign is positive or zero.
Include zeros: \( x=-2,0,4 \).
So solution: \( (-\infty, -2] \cup [0, 4] \).
✅ Answer: (D)
▶️ Answer/Explanation
Step 1: Find the zeros of the polynomial
The polynomial is \( p(x) = -x(x-4)(x+2) \).
Setting each factor equal to zero gives the zeros
\( x = -2 \), \( x = 0 \), and \( x = 4 \).
Step 2: Determine the sign of \(p(x)\) on each interval
These zeros divide the number line into intervals.
For \( x < -2 \) (e.g. \(x=-3\)):
\( -x > 0 \), \( x-4 < 0 \), \( x+2 < 0 \), so \( p(x) > 0 \).
For \( -2 < x < 0 \) (e.g. \(x=-1\)):
\( -x > 0 \), \( x-4 < 0 \), \( x+2 > 0 \), so \( p(x) < 0 \).
For \( 0 < x < 4 \) (e.g. \(x=1\)):
\( -x < 0 \), \( x-4 < 0 \), \( x+2 > 0 \), so \( p(x) > 0 \).
For \( x > 4 \) (e.g. \(x=5\)):
\( -x < 0 \), \( x-4 > 0 \), \( x+2 > 0 \), so \( p(x) < 0 \).
Step 3: Include endpoints
Since the question asks for \( p(x) \ge 0 \), include the zeros
\( x = -2, 0, 4 \).
\textbf{Step 4: Write the solution}
\( p(x) \ge 0 \) on
\( (-\infty, -2] \cup [0, 4] \).
\(\boxed{\text{Correct answer: (D)}}\)
▶️ Answer/Explanation
Factor the numerator: $x^2 + 4x – 32 = (x+8)(x-4)$.
Identify critical points where the expression is zero or undefined: $x = -8, x = 4,$ and $x = -4$.
Note that $x \neq -4$ because the denominator cannot be zero.
Test the intervals on a number line: $(-\infty, -8]$, $[-8, -4)$, $(-4, 4]$, and $[4, \infty)$.
For $x \in [-8, -4)$, the expression is positive or zero.
For $x \in [4, \infty)$, the expression is positive or zero.
The final solution set is $[-8, -4) \cup [4, \infty)$, which matches option a.
▶️ Answer/Explanation
Rearrange the inequality to $x^4 + x^3 – 12x^2 + 4x + 16 > 0$.
Testing integer roots, we find that $(x + 4)$ and $(x + 1)$ are factors.
The expression factors into $(x + 4)(x + 1)(x – 2)^2 > 0$.
The critical points where the expression equals zero are $x = -4$, $x = -1$, and $x = 2$.
The term $(x – 2)^2$ is always positive except at $x = 2$, where it is zero.
The sign of the expression depends on $(x + 4)(x + 1)$ being greater than zero.
This occurs when $x < -4$ or $x > -1$, but we must exclude $x = 2$ because the inequality is strict.
Therefore, the solution is a.$(-\infty, -4) \cup (-1, 2) \cup (2, \infty)$.
▶️ Answer/Explanation
To determine the intervals where \( k(x) \geq 0 \), we analyze the sign of the rational function.
1. Find the critical points where the numerator is zero or the denominator is zero. The numerator is zero at \( x = 3 \) and \( x = -2 \). The denominator is zero at \( x = 5 \).
2. Observe that the term \( -2(x-3)^2 \) is always less than or equal to zero because \( (x-3)^2 \geq 0 \) and multiplying by -2 makes it non-positive.
3. For the entire function \( k(x) \) to be greater than or equal to zero (positive), the remaining part of the expression, \( \frac{x+2}{x-5} \), must be less than or equal to zero (negative), so that negative \(\times\) negative = positive.
4. Solve the inequality \( \frac{x+2}{x-5} \leq 0 \). This fraction is negative when the numerator and denominator have opposite signs, which occurs in the interval between the roots: \( -2 \leq x < 5 \).
5. Check the boundary points: At \( x = -2 \), \( k(x) = 0 \), which is valid. At \( x = 5 \), the function is undefined, so we exclude it (use a parenthesis).
6. We must also ensure \( x = 3 \) is included since \( k(3) = 0 \), satisfying \( k(x) \geq 0 \). Since 3 is already inside the interval \( [-2, 5) \), our interval is complete.
Therefore, the correct interval is \( [-2, 5) \).
Correct Option: (A)
▶️ Answer/Explanation
1. Factor (D): \(x^2-4=(x-2)(x+2)\), and \(x^2-x-6=(x-3)(x+2)\).
2. The common factor \((x+2)\) cancels, producing a hole at \(x=-2\).
3. The simplified function is \( \dfrac{x-2}{x-3} \), so \(x=3\) is a vertical asymptote.
4. The numerator gives an \(x\)-intercept at \(x=2\).
5. Since numerator and denominator have equal degree, the horizontal asymptote is \(y=1\).
6. Other choices have no common factor, so they have no hole.
7. Therefore, only choice (D) satisfies all four conditions.
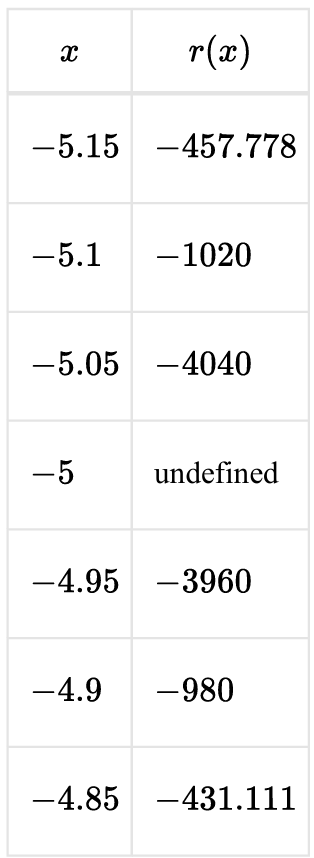
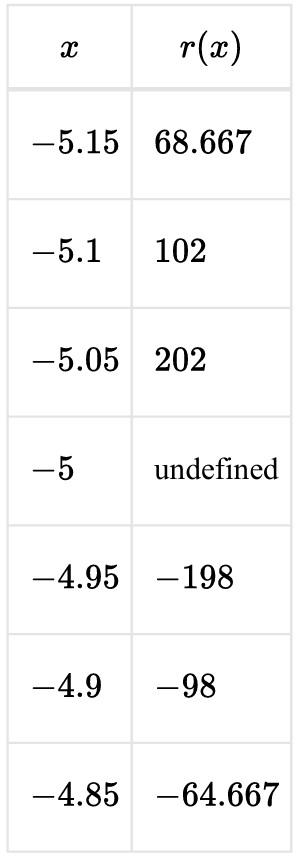
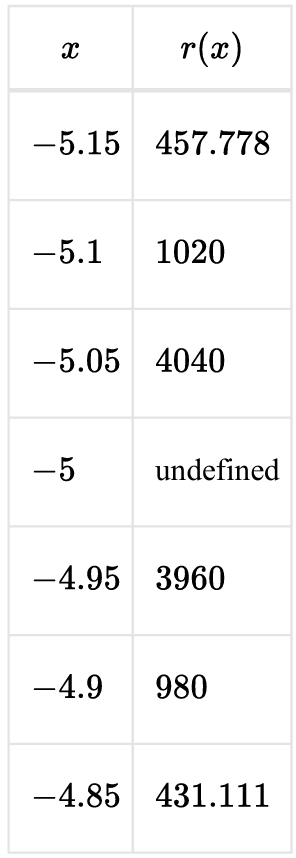
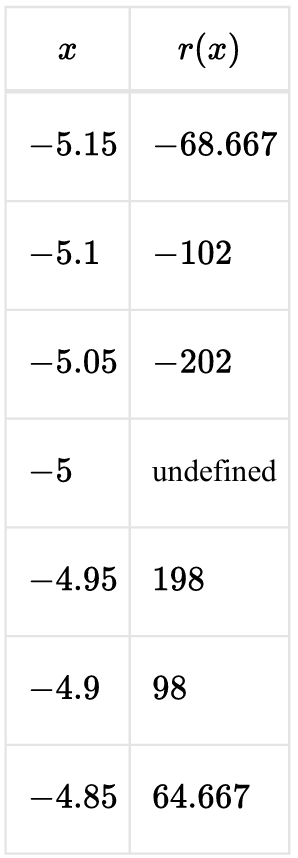
▶️ Answer/Explanation
Explanation:
The function is \( r(x) = \dfrac{2x}{(x+5)^2} \). The denominator is zero when \( x = -5 \), so the function is undefined at \( x = -5 \). Since \( (x+5)^2 \) is always positive (except at \( x = -5 \)), the sign of \( r(x) \) depends only on \( 2x \). For \( x < 0 \), \( 2x < 0 \), so \( r(x) \) must be negative on both sides of \( -5 \). Therefore, values near \( -5 \) must be large negative numbers, which matches Option (B).
1. Given \( r(x) = \dfrac{2x}{(x+5)^2} \).
2. At \( x = -5 \), denominator \( (x+5)^2 = 0 \), so undefined.
3. Since \( (x+5)^2 > 0 \) for \( x \ne -5 \), sign depends on \( 2x \).
4. For \( x < 0 \), \( 2x < 0 \), so \( r(x) < 0 \).
5. Near \( x = -5 \), denominator is very small, so magnitude becomes very large.
6. Thus outputs near \( -5 \) must be large negative values.
7. Only Option (B) satisfies these conditions.
▶️ Answer/Explanation
Explanation:
The domain of a rational function excludes values that make the denominator equal to zero. Factor \( g(x) \): \[ g(x) = x^3 – 3x^2 – 18x = x(x^2 – 3x – 18) \] \[ = x(x – 6)(x + 3) \] Thus, \( g(x) = 0 \) when \( x = 0, 6, -3 \). These values must be excluded from the domain. Therefore, the domain is all real numbers except \[ x \ne -3, \; 0, \; 6. \]
1. \( k(x) = \dfrac{h(x)}{g(x)} \), so denominator cannot be zero.
2. Factor \( g(x) = x^3 – 3x^2 – 18x \).
3. \( g(x) = x(x^2 – 3x – 18) \).
4. \( x^2 – 3x – 18 = (x – 6)(x + 3) \).
5. Thus, \( g(x) = x(x – 6)(x + 3) \).
6. Denominator equals zero at \( x = 0, 6, -3 \).
7. These values are excluded from the domain.
8. Domain: all real numbers where \( x \ne -3, 0, 6 \).
▶️ Answer/Explanation
A rational function equals zero when its numerator equals zero and its denominator is non-zero.
1. \( r(x) = 0 \Rightarrow x^3 – 4x + 3 = 0 \).
2. Test rational roots: \( x = 1 \) gives \( 1 – 4 + 3 = 0 \).
3. Factor: \( x^3 – 4x + 3 = (x – 1)(x^2 + x – 3) \).
4. Solve \( x^2 + x – 3 = 0 \).
5. \( x = \frac{-1 \pm \sqrt{1 + 12}}{2} = \frac{-1 \pm \sqrt{13}}{2} \).
6. Approximate roots: \( x \approx 1.303 \), \( x \approx -2.303 \).
7. Denominator \( x^4 + 2x – 4 \neq 0 \) at these values.
8. Therefore zeros are \( x = -2.303,\; 1.000,\; 1.303 \).
Hence, the correct option is (C).
▶️ Answer/Explanation
1. Factor the numerator:
\[ x^2+3x = x(x+3), \quad x^2-4x-5 = (x-5)(x+1). \] 2. So, \[ g(x)=\frac{x(x+3)(x-5)(x+1)}{(x+3)(x-1)(x-2)}. \] 3. Cancel the common factor \( (x+3) \) (but \( x \neq -3 \)).
4. Zeros occur when the numerator equals \(0\) and denominator is nonzero.
5. Set remaining numerator equal to zero: \[ x(x-5)(x+1)=0. \] 6. Thus \( x=0,\; 5,\; -1 \). These are not excluded values.
7. Therefore, the zeros are \( -1, 0, 5 \) only.
A rational function equals \(0\) when its numerator equals \(0\) while the denominator is not \(0\). After factoring and canceling common factors, the valid solutions are \(x=-1, 0, 5\). The value \(x=-3\) is excluded because it makes the denominator \(0\), so it is not a zero of the function.
▶️ Answer/Explanation
2. Critical points: \( x = -3, -2, 0, 3 \).
3. Sign of numerator depends on \( x \) (since \( (x+2)^2 \ge 0 \)).
4. Denominator is positive for \( x < -3 \) and \( x > 3 \), negative for \( -3 < x < 3 \).
5. Sign analysis shows \( r(x) > 0 \) on \( (-3,0) \) and \( (3,\infty) \).
6. Since \( r(x)=0 \) at \( x=-2 \) and \( x=0 \), include these values.
7. Exclude \( x=-3 \) and \( x=3 \) (undefined).
8. Therefore, solution is \( -3 < x \le 0 \) and \( x > 3 \).
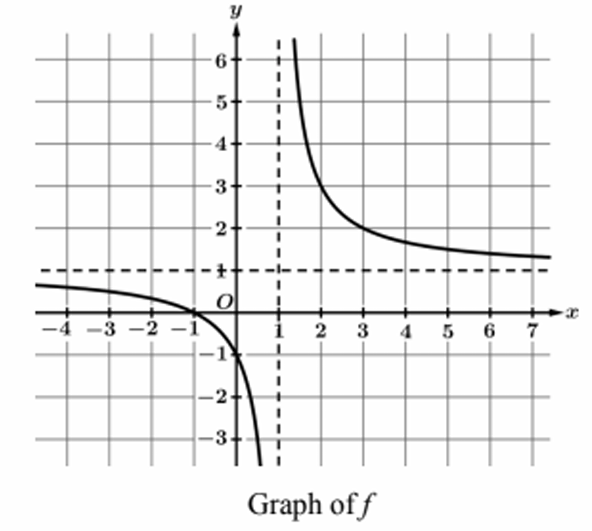
▶️ Answer/Explanation
(A)(i) Find \( h(3) \)
The function is defined as \( h(x) = g(f(x)) \).
First, we find the value of the inner function, \( f(3) \).
According to the problem text and graph, the point \( (3, 2) \) lies on the graph of \( f \). Therefore, \( f(3) = 2 \).
Now, substitute this value into the outer function \( g(x) \):
\( h(3) = g(2) \)
Using the definition \( g(x) = 2 + 3\ln x \):
\( g(2) = 2 + 3\ln(2) \)
Using a calculator to approximate \( \ln(2) \approx 0.693 \):
\( g(2) = 2 + 3(0.6931…) \approx 2 + 2.079 = 4.079 \)
Answer: \( h(3) \approx 4.079 \)
(A)(ii) Find real zeros of \( f \)
A real zero of a function occurs where the graph intersects the x-axis (where \( f(x) = 0 \)).
Looking at the provided graph, the curve intersects the x-axis at \( x = -1 \).
The problem text confirms the point \( (-1, 0) \) is on the graph.
There are no other intersections with the x-axis shown.
Answer: \( x = -1 \)
(B)(i) Find \( x \) for \( g(x) = e \)
Set up the equation:
\( 2 + 3\ln x = e \)
Subtract 2 from both sides:
\( 3\ln x = e – 2 \)
Divide by 3:
\( \ln x = \frac{e – 2}{3} \)
Convert from logarithmic to exponential form to solve for \( x \):
\( x = e^{\left(\frac{e – 2}{3}\right)} \)
Approximating the value (using \( e \approx 2.718 \)):
\( x \approx e^{0.2394} \)
Answer: \( x \approx 1.271 \)
(B)(ii) End behavior of \( g \)
We need to evaluate the limit as \( x \to \infty \) for \( g(x) = 2 + 3\ln x \).
As \( x \) increases without bound (\( x \to \infty \)), the natural logarithm function \( \ln x \) also increases without bound (\( \ln x \to \infty \)).
Multiplying by 3 and adding 2 does not change the unbounded nature.
Answer: \( \lim_{x \to \infty} g(x) = \infty \)
(C)(i) Is \( f \) invertible?
Answer: Yes, \( f \) is invertible.
(C)(ii) Reason
A function is invertible if and only if it is one-to-one. This can be verified visually using the Horizontal Line Test.
Looking at the graph of \( f(x) \):
1. The function is strictly decreasing on both branches of its domain (\( x < 1 \) and \( x > 1 \)).
2. The range of the left branch appears to be \( (-\infty, 1) \) and the range of the right branch appears to be \( (1, \infty) \).
Because the y-values do not repeat (no horizontal line intersects the graph more than once), the function is one-to-one.
Therefore, \( f \) has an inverse.