AP Precalculus -1.9 Rational Functions and Vertical Asymptotes- Study Notes - Effective Fall 2023
AP Precalculus -1.9 Rational Functions and Vertical Asymptotes- Study Notes – Effective Fall 2023
AP Precalculus -1.9 Rational Functions and Vertical Asymptotes- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Determine vertical asymptotes of graphs of rational functions.
Key Concepts:
- Vertical Asymptotes of Rational Functions
- Behavior of Rational Functions Near a Vertical Asymptote
Vertical Asymptotes of Rational Functions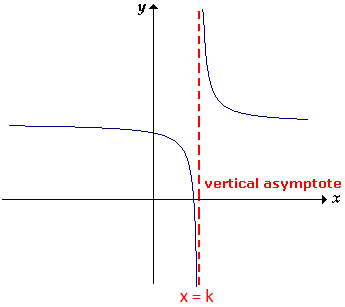
Let a rational function be written as
\( r(x) = \dfrac{p(x)}{q(x)} \)
where \( p(x) \) and \( q(x) \) are polynomial functions and \( q(x) \ne 0 \).
If a real number \( a \) is a real zero of the denominator but is not a real zero of the numerator, then the graph of the rational function has a vertical asymptote at
\( x = a \)
At a vertical asymptote, the output values of the rational function increase or decrease without bound as \( x \) approaches \( a \).
Multiplicity and Vertical Asymptotes
A vertical asymptote also occurs at \( x = a \) if the multiplicity of \( a \) as a real zero in the denominator is greater than its multiplicity as a real zero in the numerator.
This means that after simplifying the rational function, a factor of \( (x – a) \) remains in the denominator.
If the multiplicities are equal, the factor cancels completely and the graph has a hole instead of a vertical asymptote.
Example:
Identify the vertical asymptotes of the rational function
\( r(x) = \dfrac{x + 2}{(x – 1)(x + 3)} \)
▶️ Answer/Explanation
The denominator is zero at \( x = 1 \) and \( x = -3 \).
Neither factor appears in the numerator, so neither cancels.
Conclusion
The graph has vertical asymptotes at \( x = 1 \) and \( x = -3 \).
Example:
Determine whether the rational function has a vertical asymptote or a hole at \( x = 2 \):
\( f(x) = \dfrac{(x – 2)^2}{(x – 2)^3} \)
▶️ Answer/Explanation
The multiplicity of \( x = 2 \) in the numerator is 2.
The multiplicity of \( x = 2 \) in the denominator is 3.
After simplifying, one factor of \( (x – 2) \) remains in the denominator.
Conclusion
The graph has a vertical asymptote at \( x = 2 \).
Behavior of Rational Functions Near a Vertical Asymptote
Let \( r(x) = \dfrac{p(x)}{q(x)} \) be a rational function, and suppose the graph has a vertical asymptote at \( x = a \).
Near a vertical asymptote, the values of the polynomial in the denominator, \( q(x) \), become arbitrarily close to zero.
As a result, the values of the rational function \( r(x) \) increase or decrease without bound.
The behavior of the function depends on whether \( x \) approaches \( a \) from the right or from the left.
Right-Hand Behavior

\( \lim_{x \to a^{+}} r(x) = \infty \)
or
\( \lim_{x \to a^{+}} r(x) = -\infty \)
This describes the behavior of the function for input values greater than \( a \) and close to \( a \).
Left-Hand Behavior
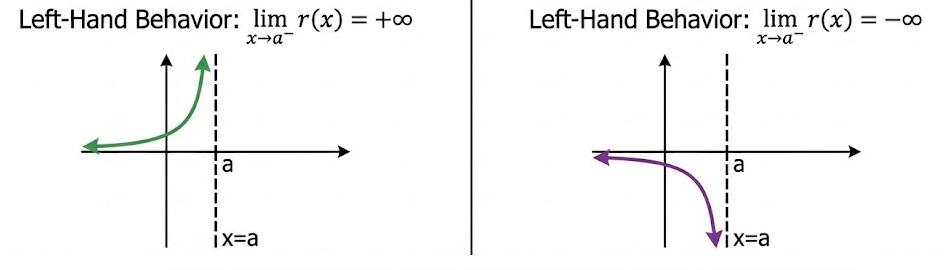
\( \lim_{x \to a^{-}} r(x) = \infty \)
or
\( \lim_{x \to a^{-}} r(x) = -\infty \)
This describes the behavior of the function for input values less than \( a \) and close to \( a \).
The signs depend on whether the denominator approaches zero through positive or negative values.
Example:
Consider the rational function
\( r(x) = \dfrac{1}{x – 2} \)
Describe the behavior near the vertical asymptote.
▶️ Answer/Explanation
The denominator is zero at \( x = 2 \), so there is a vertical asymptote at \( x = 2 \).
For \( x \to 2^{+} \), the denominator is positive and very small.
\( \lim_{x \to 2^{+}} r(x) = \infty \)
For \( x \to 2^{-} \), the denominator is negative and very small.
\( \lim_{x \to 2^{-}} r(x) = -\infty \)
Example:
Analyze the behavior near the vertical asymptote of
\( f(x) = \dfrac{-2}{x + 3} \)
▶️ Answer/Explanation
The vertical asymptote occurs at \( x = -3 \).
For \( x \to -3^{+} \), the denominator is positive and close to zero.
\( \lim_{x \to -3^{+}} f(x) = -\infty \)
For \( x \to -3^{-} \), the denominator is negative and close to zero.
\( \lim_{x \to -3^{-}} f(x) = \infty \)
