AP Precalculus -2.1 Arithmetic and Geometric Sequences- MCQ Exam Style Questions - Effective Fall 2023
AP Precalculus -2.1 Arithmetic and Geometric Sequences- MCQ Exam Style Questions – Effective Fall 2023
AP Precalculus -2.1 Arithmetic and Geometric Sequences- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.
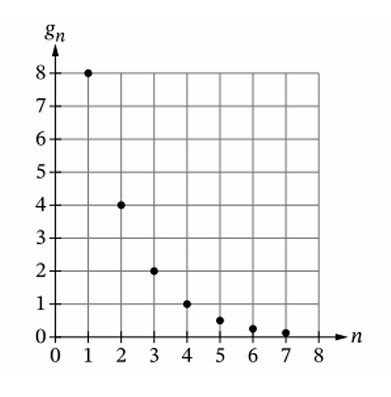
Question
(B) \( g_n = 8(2)^{(n-1)} \)
(C) \( g_n = 8 \left( \frac{1}{2} \right)^n \)
(D) \( g_n = 16 \left( \frac{1}{2} \right)^{(n-1)} \)
▶️ Answer/Explanation
From the graph, likely \( g_1 = 8 \), \( g_2 = 4 \), so common ratio \( r = \frac{4}{8} = \frac{1}{2} \).
General form: \( g_n = g_1 \cdot r^{\,n-1} = 8 \cdot \left( \frac{1}{2} \right)^{n-1} \).
But none match exactly — check options:
(A) \( 4 \left( \frac{1}{2} \right)^{n-2} = 4 \cdot \left( \frac{1}{2} \right)^{n-2} = 8 \cdot \left( \frac{1}{2} \right)^{n-1} \), yes, because \( 4 \cdot \left( \frac{1}{2} \right)^{-1} = 4 \cdot 2 = 8 \).
So (A) is equivalent to the standard form.
✅ Answer: (A)
Question
(B) The exponential function \( C(x) = s \cdot p^x \) for \( 1 \leq x \leq 8 \)
(C) The arithmetic sequence \( C_n = s + pn \) for \( 1 \leq n \leq 8 \)
(D) The geometric sequence \( C_n = s \cdot p^n \) for \( 1 \leq n \leq 8 \)
▶️ Answer/Explanation
Possible costs depend on the number of plants \( n \), where \( n \) is an integer from 1 to 8.
Total cost = shovel cost + \( n \) × plant cost = \( s + pn \).
This describes a set of discrete values (not a continuous function) because \( n \) is an integer.
An arithmetic sequence with first term \( s+p \) and common difference \( p \) models this exactly: \( C_n = s + pn \), \( n = 1,2,\dots,8 \).
✅ Answer: (C)
Question
(B) The linear function \( f(n) = 2 + 4(n – 1) \)
(C) The geometric sequence \( g_n = 2^{(n-1)} \)
(D) The exponential function \( h(n) = 2 \cdot 2^{(n-1)} \)
▶️ Answer/Explanation
Test each option with inputs \( n = 2 \) and \( n = 3 \):
(A) \( a_2 = 4 \cdot 2 = 8 \) ❌ (needs 4)
(B) \( f(2) = 2 + 4(2-1) = 6 \) ❌ (needs 4)
(C) \( g_2 = 2^{1} = 2 \) ❌ (needs 4)
(D) \( h(2) = 2 \cdot 2^{1} = 4 \), \( h(3) = 2 \cdot 2^{2} = 8 \) ✅
So \( h(n) = 2 \cdot 2^{(n-1)} \) matches both points.
✅ Answer: (D)
Question
(B) If the sequence is arithmetic, the third term could be \( 12 \).
(C) If the sequence is geometric, the fifth term could be \( 48 \).
(D) If the sequence is arithmetic, the sixth term could be \( 48 \).
▶️ Answer/Explanation
Let’s analyze both possibilities:
Geometric: Let \( a_2 = ar = 6 \), \( a_4 = ar^3 = 24 \). Dividing: \( r^2 = 4 \) so \( r = 2 \) or \( r = -2 \).
If \( r = 2 \), \( a = 3 \), terms: 3, 6, 12, 24, 48 → (C) says 5th term could be 48, which is true.
If \( r = -2 \), \( a = -3 \), terms: -3, 6, -12, 24, -48 → 5th term is -48, but “could be” allows for the positive case.
Arithmetic: Let \( a_2 = a + d = 6 \), \( a_4 = a + 3d = 24 \). Subtract: \( 2d = 18 \) so \( d = 9 \), \( a = -3 \). Terms: -3, 6, 15, 24, 33, 42 → (D) says 6th term could be 48, which is false.
Check (A): If geometric and first term 1, then \( r = 6 \) so 4th term \( 1 \cdot r^3 = 216 \), not 24 ❌
Check (B): Arithmetic third term: \( a_3 = a_2 + d = 6 + 9 = 15 \), not 12 ❌
✅ Answer: (C)
Question
(B) \( 17 + 3n \)
(C) \( 21 + 3n \)
(D) \( 51 \cdot 3^{(n-10)} \)
▶️ Answer/Explanation
Simplify \( a_n = 51 + 3(n – 10) \):
\( a_n = 51 + 3n – 30 = 21 + 3n \).
This matches option (C).
Check initial term \( a_0 = 21 \) (since \( a_0 \) is given as the initial value in the problem statement).
✅ Answer: (C)
Question
(B) 26,192
(C) 14,000
(D) 611
▶️ Answer/Explanation
Geometric sequence: \( a_n = a_1 r^{n-1} \).
Given \( a_4 = 4000 \), \( a_8 = 49000 \).
\[ a_8 = a_4 r^{4} \quad \Rightarrow \quad 49000 = 4000 r^4 \]
\[ r^4 = \frac{49000}{4000} = 12.25 \]
\[ r = (12.25)^{1/4} = \sqrt{\sqrt{12.25}} = \sqrt{3.5} \approx 1.870828693 \]
Then \( a_6 = a_4 r^{2} = 4000 \times (12.25)^{1/2} = 4000 \times 3.5 = 14000 \).
✅ Answer: (C)
Question
▶️ Answer/Explanation
The common ratio is $r = \frac{a_5}{a_4} = \frac{64}{32} = 2$.
Using the formula $a_n = a_1 \cdot r^{n-1}$, we find $a_4 = a_1 \cdot 2^{4-1}$.
Substitute the known values: $32 = a_1 \cdot 2^3$, which means $32 = a_1 \cdot 8$.
Solving for the first term gives $a_1 = \frac{32}{8} = 4$.
The explicit formula is $a_n = 4 \cdot 2^{n-1}$.
Comparing this to the given options, the correct choice is c.
Question
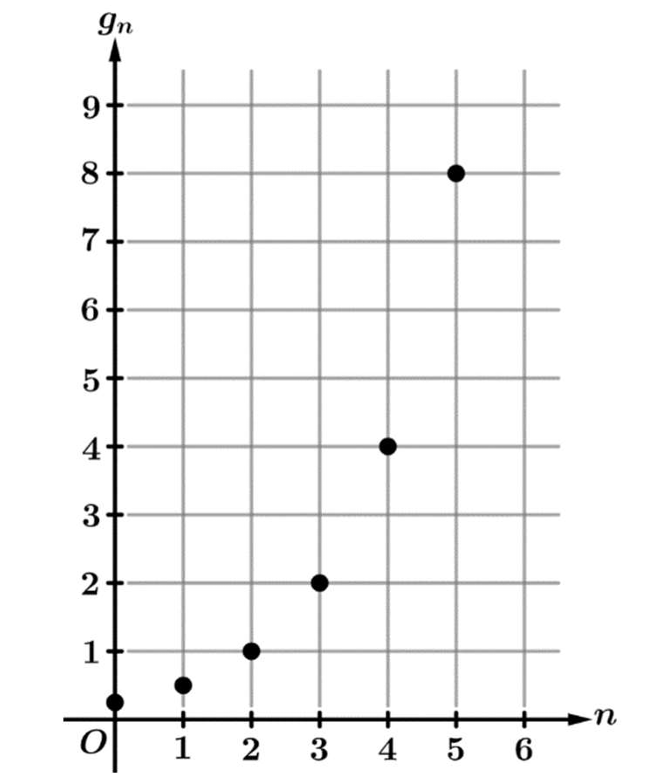
▶️ Answer/Explanation
From the graph, we observe the points: \( (2, 1) \), \( (3, 2) \), \( (4, 4) \), and \( (5, 8) \).
This shows a geometric sequence with a common ratio of \( 2 \) (e.g., \( \frac{4}{2} = 2 \)).
We test the options by substituting \( n = 2 \), knowing that \( g_2 \) must equal \( 1 \):
(A) \( \frac{1}{4}\left(\frac{1}{2}\right)^2 = \frac{1}{4} \cdot \frac{1}{4} = \frac{1}{16} \) (Incorrect)
(B) \( \frac{1}{2} \cdot 2^2 = \frac{1}{2} \cdot 4 = 2 \) (Incorrect)
(C) \( (2)^{2-1} = 2^1 = 2 \) (Incorrect)
(D) \( 4(2)^{2-4} = 4(2)^{-2} = 4\left(\frac{1}{4}\right) = 1 \) (Correct)
Therefore, the correct expression is \( 4(2)^{n-4} \).
Question
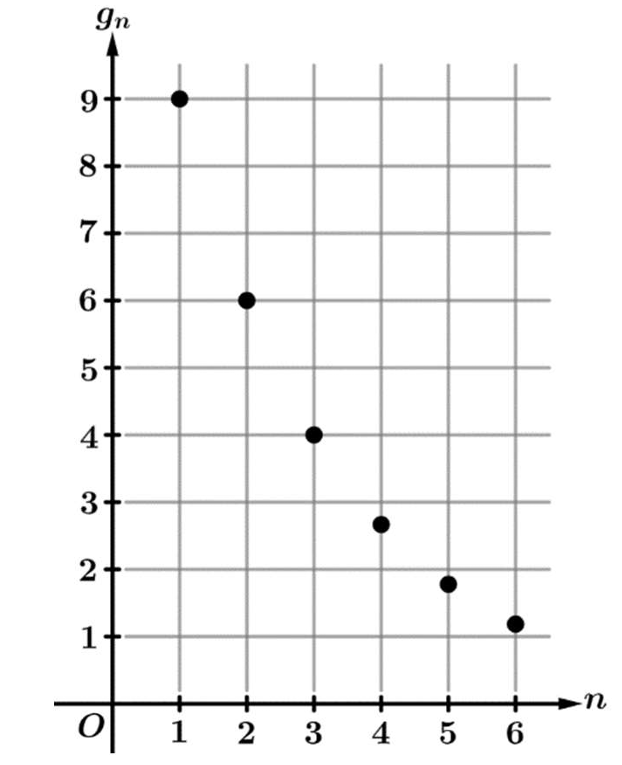
▶️ Answer/Explanation
From the graph, we can identify the coordinates of the first few terms: \((1, 9)\), \((2, 6)\), and \((3, 4)\).
This gives us the first term \(a_1 = 9\) and the second term \(a_2 = 6\).
Calculate the common ratio \(r\) of the geometric sequence: \(r = \frac{a_2}{a_1} = \frac{6}{9} = \frac{2}{3}\).
The standard formula for the \(n\)th term is \(g_n = a_1 \cdot r^{n-1}\), which gives \(g_n = 9\left(\frac{2}{3}\right)^{n-1}\).
To find the matching option, we can substitute a known point like \(n=3\) (where \(g_3 = 4\)) into the choices.
Checking Option (D): \(4\left(\frac{2}{3}\right)^{3-3} = 4\left(\frac{2}{3}\right)^0 = 4(1) = 4\). This matches the graph perfectly.
Algebraically, we can also rewrite the standard formula to match Option (D): \(9\left(\frac{2}{3}\right)^{n-1} = 9\left(\frac{2}{3}\right)^2 \left(\frac{2}{3}\right)^{n-3} = 9 \cdot \frac{4}{9} \cdot \left(\frac{2}{3}\right)^{n-3} = 4\left(\frac{2}{3}\right)^{n-3}\).
Thus, the correct expression is (D).
Question
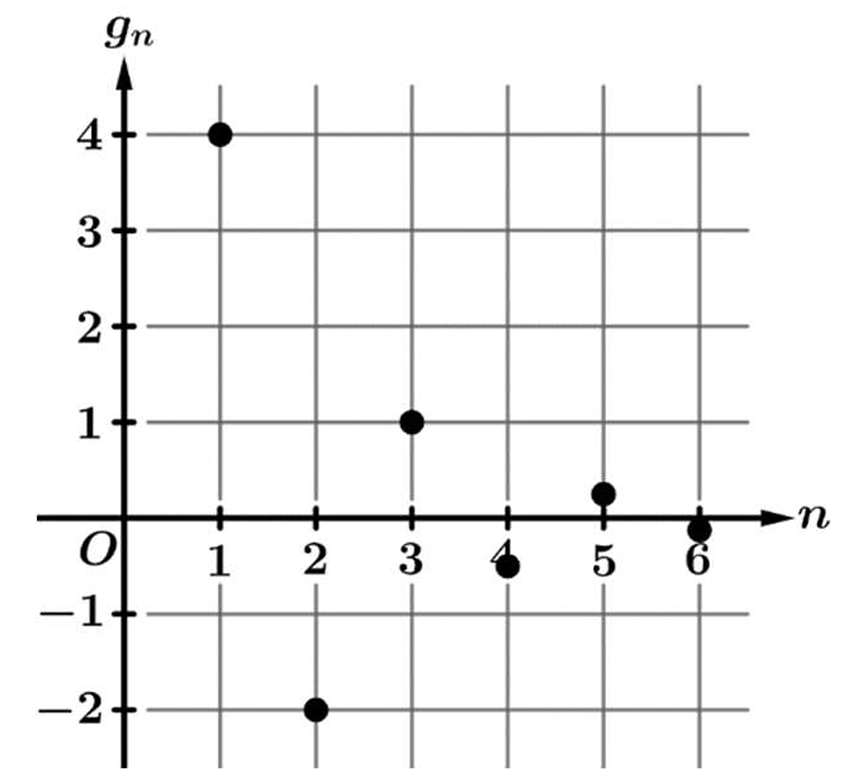
▶️ Answer/Explanation
From the graph, we identify the coordinates of the first few terms as \((1, 4)\), \((2, -2)\), and \((3, 1)\).
The first term of the sequence is \(g_1 = 4\).
We find the common ratio \(r\) by dividing the second term by the first: \(r = \frac{g_2}{g_1} = \frac{-2}{4} = -\frac{1}{2}\).
Verifying with the third term: \(g_3 = -2 \times (-\frac{1}{2}) = 1\), which matches the graph.
The general formula for a geometric sequence is \(g_n = a_1 \cdot r^{n-1}\).
Substituting our values, we get \(g_n = 4 \cdot {\left(-\frac{1}{2}\right)}^{n-1}\).
Comparing this result with the options, it matches option (B).
Correct Answer: (B)
Question
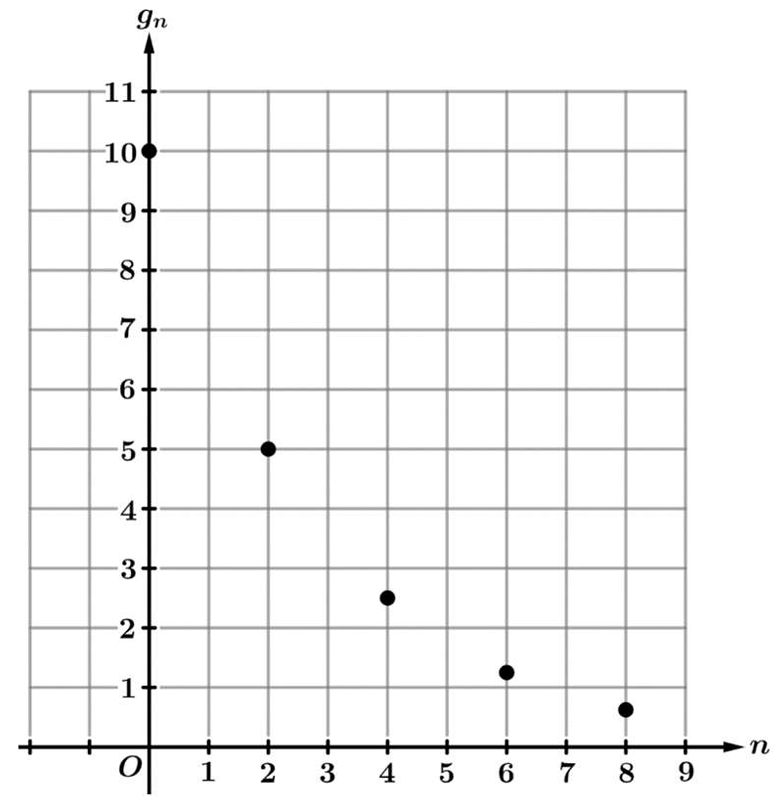
▶️ Answer/Explanation
From the graph, we identify two key points: \( (0, 10) \) and \( (2, 5) \). This means \( g_0 = 10 \) and \( g_2 = 5 \).
We test each option by substituting \( n = 0 \) first to check the initial value:
(A) \( n=0 \to 5(1/2)^0 = 5 \). Incorrect, as \( g_0 \neq 10 \).
(B) \( n=0 \to 5(1/2)^{-2} = 5(4) = 20 \). Incorrect, as \( g_0 \neq 10 \).
(C) \( n=0 \to 10(1/2)^0 = 10 \). Correct. Now check \( n=2 \to 10(1/2)^1 = 5 \). Correct.
(D) \( n=0 \to 10(1/2)^0 = 10 \). Correct. Now check \( n=2 \to 10(1/2)^4 = 10/16 \neq 5 \). Incorrect.
Thus, the correct expression matches the graph values in option (C).
Question
▶️ Answer/Explanation
Let the number of seats in row \(n\) be denoted by \(a_n\) and the common difference by \(d\).
We are given \(a_4 = 30\) and \(a_8 = 54\).
Using the arithmetic sequence formula differences \(a_8 – a_4 = (8-4)d\):
\(54 – 30 = 4d \Rightarrow 24 = 4d \Rightarrow d = 6\).
To find the number of seats in the tenth row (\(a_{10}\)), we calculate:
\(a_{10} = a_4 + (10-4)d\)
\(a_{10} = 30 + 6(6) = 30 + 36 = 66\).
Therefore, the correct answer is (B).
Question
▶️ Answer/Explanation
The relationship between any two terms in an arithmetic sequence is \( a_m = a_n + (m-n)d \).
First, substitute the given values \( a_6 = 10 \) and \( a_3 = 22 \) to find the common difference \( d \):
\( 10 = 22 + (6 – 3)d \implies 10 = 22 + 3d \).
Solving for \( d \): \( 3d = 10 – 22 = -12 \implies d = -4 \).
Now, solve for \( a_{12} \) using the term \( a_3 \) and the difference \( d = -4 \):
\( a_{12} = a_3 + (12 – 3)d = 22 + 9(-4) \).
\( a_{12} = 22 – 36 = -14 \).
Therefore, the correct option is (B).
Question
| \(n\) | 0 | 1 | 2 | 3 | 4 |
| \(s_n\) | 12 | 6 | 0 | \(-6\) | \(-12\) |
▶️ Answer/Explanation
To identify the type of sequence, we analyze the relationship between consecutive terms in the table.
First, calculate the difference between the first two terms: \(6 – 12 = -6\).
Next, calculate the difference between the second and third terms: \(0 – 6 = -6\).
Checking the remaining terms confirms the pattern: \(-6 – 0 = -6\) and \(-12 – (-6) = -6\).
Since the difference between successive terms is a constant value (\(d = -6\)), the sequence is arithmetic.
By definition, an arithmetic sequence is characterized by a constant difference, not proportional change.
Therefore, the correct statement is that \(s_n\) could be an arithmetic sequence due to the constant difference.
Question
| \(n\) | 2 | 3 | 4 | 5 | 6 |
| \(s_n\) | 1 | 2 | 4 | 8 | 16 |
▶️ Answer/Explanation
To determine the type of sequence, we analyze the relationship between consecutive terms of \(s_n\): \(1, 2, 4, 8, 16\).
First, check for an arithmetic sequence by looking for a constant difference: \(2-1=1\), \(4-2=2\). Since \(1 \neq 2\), it is not arithmetic.
Next, check for a geometric sequence by looking for a constant ratio (proportional change): \(\frac{2}{1} = 2\), \(\frac{4}{2} = 2\), \(\frac{8}{4} = 2\).
The sequence has a constant common ratio \(r = 2\).
A sequence with a constant proportional change between terms is defined as a geometric sequence.
Therefore, \(s_n\) is a geometric sequence because successive terms have a constant proportional change.
Correct Option: (D)
Question
| \(n\) | \(1\) | \(5\) | \(7\) | \(8\) | \(15\) |
| \(a_n\) | \(b\) | \(32\) | \(26\) | \(c\) | \(2\) |
▶️ Answer/Explanation
First, find the common difference \(d\) using the known terms \(a_5 = 32\) and \(a_7 = 26\):
\(a_7 = a_5 + 2d \implies 26 = 32 + 2d \implies -6 = 2d \implies d = -3\).
Next, calculate \(b\) (which corresponds to \(a_1\)) by working backwards from \(a_5\):
\(b = a_1 = a_5 – 4d = 32 – 4(-3) = 32 + 12 = 44\).
Then, calculate \(c\) (which corresponds to \(a_8\)) using \(a_7\) and \(d\):
\(c = a_8 = a_7 + d = 26 + (-3) = 23\).
Finally, calculate the value of \(b + c\):
\(b + c = 44 + 23 = 67\).
Question
▶️ Answer/Explanation
The general formula for the \( n \)-th term of a geometric sequence is \( g_n = g_1 \cdot r^{n-1} \).
We are given \( g_1 = 3 \) and \( g_4 = 24 \). Substituting these into the formula:
\( 24 = 3 \cdot r^{4-1} \implies 24 = 3r^3 \).
Dividing both sides by 3 gives \( r^3 = 8 \).
Solving for the common ratio, we get \( r = 2 \).
Now, we calculate \( g_3 \) using \( r = 2 \) and \( n = 3 \):
\( g_3 = 3 \cdot 2^{3-1} = 3 \cdot 2^2 \).
\( g_3 = 3 \cdot 4 = 12 \).
Question
▶️ Answer/Explanation
We need to find the equation \( g_k \) such that the second term (where \( k=2 \)) equals \( ae^2 \). We verify this by substituting \( k=2 \) into each option.
(A) \( g_2 = a(e^2) = ae^2 \). This matches the given term exactly. (Also, \( k=5 \) yields \( ae^5 \)).
(B) \( g_2 = a(e)^{2-1} = ae^1 = ae \). This is incorrect.
(C) \( g_2 = a(e^2) – 2 \). This is incorrect.
(D) \( g_2 = a(e+2)^{2-1} = a(e+2) \). This is incorrect.
Since only option (A) yields the correct value \( ae^2 \) for the second term, it is the correct equation.
Question
(B) \(25\)
(C) \(972\)
(D) \(2,916\)
▶️ Answer/Explanation
The formula for the \(n\)-th term of an arithmetic sequence is given by \(a_n = a_1 + (n – 1)d\).
Here, the first term is \(a_1 = 4\), the common difference is \(d = 3\), and we need to find the seventh term (\(n = 7\)).
Substituting these values into the formula gives:
\(a_7 = 4 + (7 – 1)3\)
Simplify the expression inside the parentheses:
\(a_7 = 4 + (6)3\)
Multiply the terms:
\(a_7 = 4 + 18\)
Add to find the final result:
\(a_7 = 22\)
Question
▶️ Answer/Explanation
The discount follows a geometric sequence where the first term $a_1 = 1.5\%$ and the common ratio $r = 2$.
Exceeding the purchase price means the discount percentage must be greater than $100\%$.
Week $1$: $1.5\%$
Week $2$: $3\%$
Week $3$: $6\%$
Week $4$: $12\%$
Week $5$: $24\%$
Week $6$: $48\%$
Week $7$: $96\%$
Week $8$: $192\%$, which is the first week to exceed $100\%$.
Thus, the correct option is (C).
Question
▶️ Answer/Explanation
Question
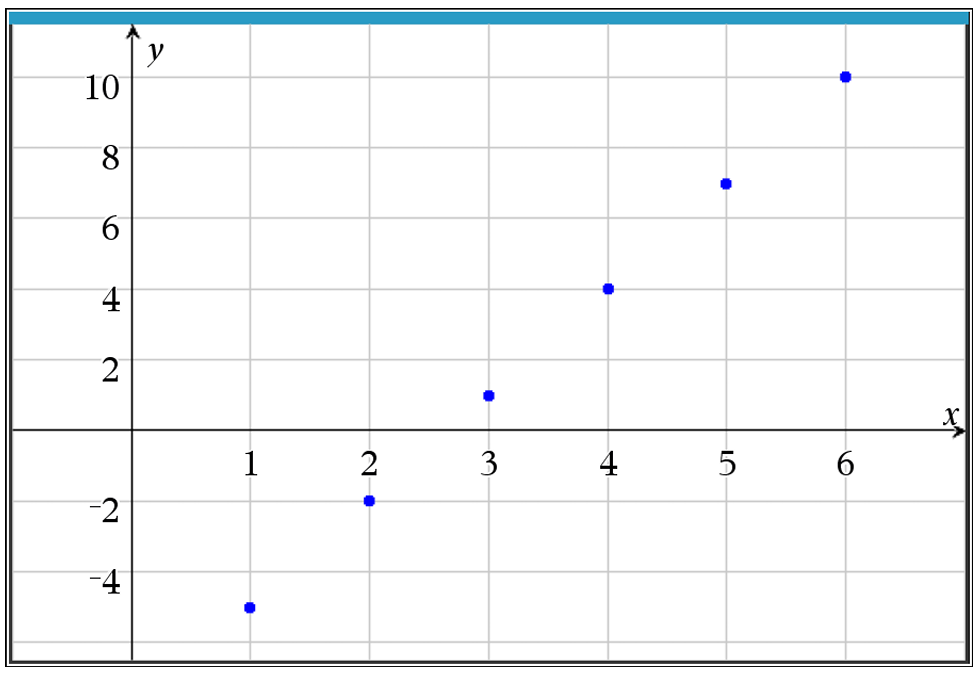
(B) $a_n = -5 + 3(n – 1)$
(C) $a_n = -5 – 3(n – 1)$
(D) $a_n = -8 – 3(n – 1)$
▶️ Answer/Explanation
Identify the first term $a_1$ from the graph at $n = 1$, which is $-5$.
Find the common difference $d$ by calculating the change between terms, such as $a_2 – a_1 = -2 – (-5) = 3$.
Recall the general formula for an arithmetic sequence: $a_n = a_1 + d(n – 1)$.
Substitute the identified values $a_1 = -5$ and $d = 3$ into the formula.
The resulting expression is $a_n = -5 + 3(n – 1)$.
Compare this result to the given options to find the match.
The correct option is (B).
Question (Calc Allowed)
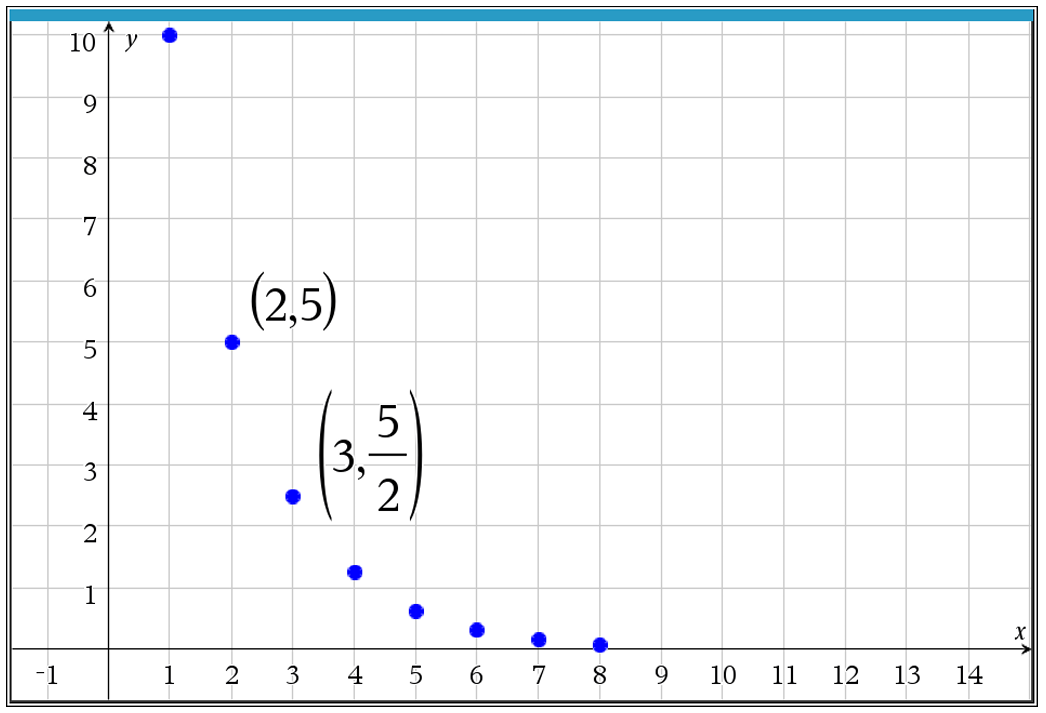
(B) $0.3125$
(C) $0.15625$
(D) $0.078125$
▶️ Answer/Explanation
Identify two consecutive terms from the graph: $g_2 = 5$ and $g_3 = \frac{5}{2}$.
Calculate the common ratio $r$ using $r = \frac{g_3}{g_2} = \frac{5/2}{5} = \frac{1}{2}$ or $0.5$.
The general formula for the $n^{th}$ term is $g_n = g_2 \cdot r^{n-2}$.
Substitute the values to find $g_6$: $g_6 = 5 \cdot (0.5)^{6-2}$.
Calculate the power: $g_6 = 5 \cdot (0.5)^4 = 5 \cdot 0.0625$.
Final calculation: $g_6 = 0.3125$.
The correct option is (B).
Question (Calc Allowed)
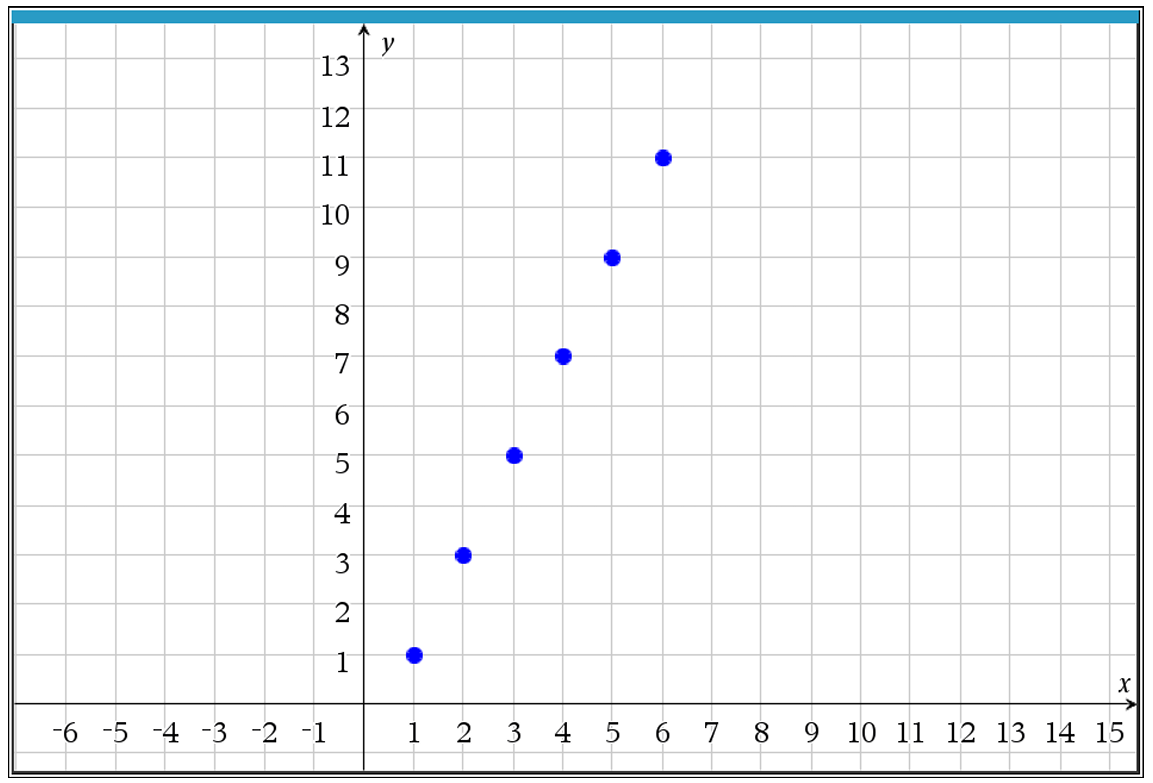
(B) $f(x) = 2 + 5(x – 3)$
(C) $f(x) = 5 – 2(x – 3)$
(D) $f(x) = 2 – 5(x – 3)$
▶️ Answer/Explanation
Identify two points from the graph: $(1, 1)$ and $(2, 3)$.
Calculate the common difference (slope) using $d = \frac{a_2 – a_1}{2 – 1} = \frac{3 – 1}{1} = 2$.
Locate the value of the sequence at $k = 3$, which is the point $(3, 5)$, so $a_3 = 5$.
Substitute $a_k = 5$, $d = 2$, and $k = 3$ into the formula $f(x) = a_k + d(x – k)$.
The resulting linear function is $f(x) = 5 + 2(x – 3)$.
Comparing this to the given choices, the correct option is (A).