AP Precalculus -2.10 Inverses of Exponential Functions- MCQ Exam Style Questions - Effective Fall 2023

AP Precalculus -2.10 Inverses of Exponential Functions- MCQ Exam Style Questions – Effective Fall 2023

AP Precalculus -2.10 Inverses of Exponential Functions- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.

AP Precalculus – MCQ Exam Style Questions- All Topics

Question

In a certain town, the population in the year 2000 was about $ 30{,}000 $. The population grows at a rate of $ 2.3\% $ per year, and time is measured in years since 2000. Which of the following functions gives output values, in years since 2000, for input values of the town’s population $ p $?

(A) $ f(p) = 30{,}000 \cdot (1.023)^p $
(B) $ g(p) = \log_{1.023} \left( \frac{p}{30{,}000} \right) $
(C) $ h(p) = \frac{p-30{,}000}{2.3} $
(D) $ k(p) = 30{,}000 \cdot \log_{1.023} p $

▶️ Answer/Explanation

Detailed solution

Population model: $ P(t) = 30{,}000 \cdot (1.023)^t $ where $ t $ = years since 2000.
We want $ t $ as a function of $ p $: solve $ p = 30{,}000 \cdot (1.023)^t $ for $ t $.
Divide: $ \frac{p}{30{,}000} = (1.023)^t $
Take $\log_{1.023}$: $ t = \log_{1.023} \left( \frac{p}{30{,}000} \right) $
This matches $ g(p) $.
✅ Answer: (B)

Question

The function $ g $ is given by $ g(x) = \frac{4x+6}{5} $. Which of the following defines $ g^{-1}(x) $?

(A) $ \frac{5}{4x+6} $
(B) $ \frac{5x+6}{4} $
(C) $ \frac{5x}{4} – 6 $
(D) $ \frac{5x-6}{4} $

▶️ Answer/Explanation

Detailed solution

Solve $ y = \frac{4x+6}{5} $ for $ x $:
Multiply by 5: $ 5y = 4x + 6 $
Subtract 6: $ 5y – 6 = 4x $
Divide by 4: $ x = \frac{5y-6}{4} $
Thus $ g^{-1}(x) = \frac{5x-6}{4} $.
✅ Answer: (D)

Question

The exponential function $ g $ is given by $ g(x) = 5^x $. Which of the following expressions defines $ g^{-1}(x) $?

(A) $ \log_5 x $
(B) $ \log_x 5 $
(C) $ \sqrt[5]{x} $
(D) $ \sqrt[5]{5} $

▶️ Answer/Explanation

Detailed solution

The inverse of $ y = 5^x $ is $ x = 5^y $ ⇒ $ y = \log_5 x $.
✅ Answer: (A)

Question

The graph of the exponential function $ f $ is given. Which of the following could be a table of values for the inverse function of $ f $?

(A) \[\begin{array}{c|c} x & f^{-1}(x) \\ \hline 5 & 25 \\ 2 & 4 \\ \end{array}\]
(B) \[\begin{array}{c|c} x & f^{-1}(x) \\ \hline 25 & 5 \\ 4 & 2 \\ \end{array}\]
(C) \[\begin{array}{c|c} x & f^{-1}(x) \\ \hline 32 & 5 \\ 4 & 2 \\ \end{array}\]
(D) \[\begin{array}{c|c} x & f^{-1}(x) \\ \hline 5 & 32 \\ 2 & 4 \\ \end{array}\]

▶️ Answer/Explanation

Detailed solution

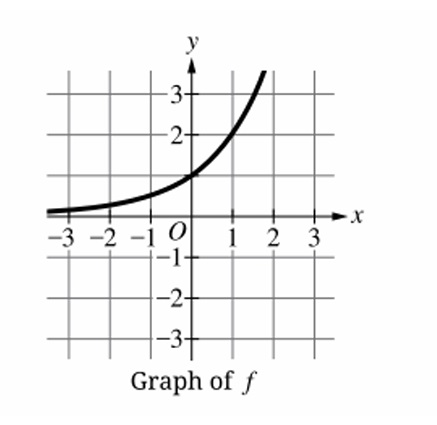
From the graph, $ f $ appears to be $ f(x) = 2^x $.
Then $ f^{-1}(x) = \log_2 x $.
Check values: $ f^{-1}(32) = \log_2 32 = 5 $, $ f^{-1}(4) = \log_2 4 = 2 $.
So table should be $ (32, 5) $ and $ (4, 2) $, which matches option (C).
✅ Answer: (C)

Question

Which of the following is the inverse of the function $ f $ given by $ f(x) = 4 \log_2(x + 3) – 1 $?

(A) $ g(x) = \frac{1}{4}(2^x + 1) – 3 $
(B) $ g(x) = \frac{1}{4} \cdot 2^{(x+1)} – 3 $
(C) $ g(x) = 2^{(\frac{x}{4}+1)} – 3 $
(D) $ g(x) = 2^{(\frac{x+1}{4})} – 3 $

▶️ Answer/Explanation

Detailed solution

Let $ y = 4 \log_2(x+3) – 1 $.
$ y+1 = 4 \log_2(x+3) $
$ \frac{y+1}{4} = \log_2(x+3) $
$ x+3 = 2^{(y+1)/4} $
$ x = 2^{(y+1)/4} – 3 $
Thus $ f^{-1}(x) = 2^{(x+1)/4} – 3 $.
✅ Answer: (D)

Question

The initial population size of an animal species is measured to be $ 2000 $. The population doubles every $ 8 $ years. Which of the following functions gives the time, in years, as an output value, and a certain number $ x $ for the population size as an input value?

(A) $ f(x) = \frac{1}{8} \log_2\left(\frac{x}{2000}\right) $
(B) $ g(x) = \log_2\left(\frac{8x}{2000}\right) $
(C) $ h(x) = 8 \log_2\left(\frac{x}{2000}\right) $
(D) $ k(x) = 2000 \log_8 x $

▶️ Answer/Explanation

Detailed solution

The exponential growth model is: $ P(t) = 2000 \cdot 2^{(t/8)} $, where $ t $ is time in years.
We want the inverse function $ t $ in terms of population $ x $.
Set $ x = 2000 \cdot 2^{(t/8)} $.
Divide both sides by $ 2000 $: $ \frac{x}{2000} = 2^{(t/8)} $.
Take log base 2: $ \log_2\left(\frac{x}{2000}\right) = \frac{t}{8} $.
Multiply by 8: $ t = 8 \log_2\left(\frac{x}{2000}\right) $.
This matches option (C).
✅ Answer: (C)

Question

The figure shows the graph of an exponential function $k$, where $k(x) = b^x$ for $b > 0$ and $b \neq 1$. Consider the logarithmic function $h$ (not shown) given by $h(x) = \log_b x$. Of which of the following pairs of points are on the graph of $h$?

(A) $(-3, -1)$ and $(-9, -2)$

(B) $(1, \frac{1}{3})$ and $(2, \frac{1}{9})$

(D) $(3, 1)$ and $(9, 2)$

▶️ Answer/Explanation

Detailed solution

The correct option is (D).

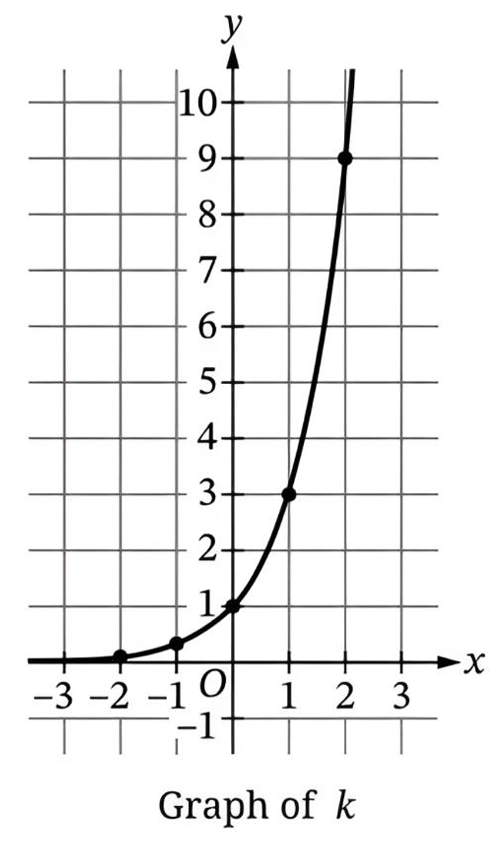
1. First, identify the base $b$ of the exponential function $k(x) = b^x$ using points from the graph.
2. The graph passes through the point $(1, 3)$. Substituting this into the equation gives $3 = b^1$, so $b = 3$.
3. The function $h$ is defined as $h(x) = \log_b x$, which becomes $h(x) = \log_3 x$.
4. Since logarithmic and exponential functions are inverses, if $(x, y)$ is on the graph of $k$, then $(y, x)$ is on the graph of $h$.
5. The graph of $k$ contains the points $(1, 3)$ and $(2, 9)$.
6. Swapping the coordinates to find points on $h$, we get $(3, 1)$ and $(9, 2)$.
7. We can verify this algebraically: $h(3) = \log_3(3) = 1$ and $h(9) = \log_3(9) = 2$.

Question

The figure shows the graph of an exponential function $k$, where $k(x) = b^x$ for $b > 0$ and $b \neq 1$. Consider the logarithmic function $h$ (not shown) given by $h(x) = \log_b x$. Of the following pairs of points, which are on the graph of $h$?

(A) $(-3, -1)$ and $(-9, -2)$

(B) $(1, \frac{1}{3})$ and $(2, \frac{1}{9})$

(D) $(3, 1)$ and $(9, 2)$

▶️ Answer/Explanation

Detailed solution

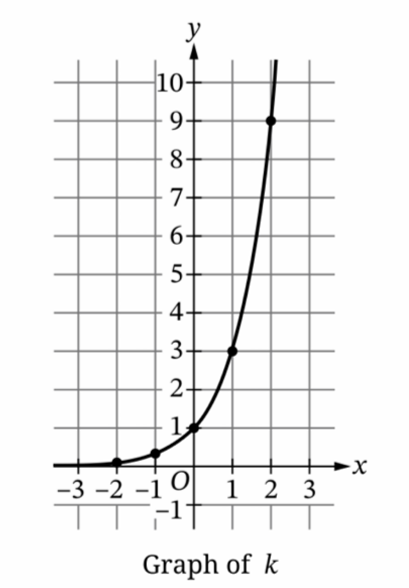
First, identify the base $b$ using a clear point on the graph of $k(x) = b^x$.
The graph passes through the point $(1, 3)$. Substituting this into the equation gives $3 = b^1$, so $b = 3$.
Therefore, the exponential function is $k(x) = 3^x$, and the logarithmic function is its inverse, $h(x) = \log_3 x$.
Since $k$ and $h$ are inverses, if a point $(x, y)$ is on $k$, then $(y, x)$ is on $h$.
The graph of $k$ clearly passes through $(1, 3)$ and $(2, 9)$.
Thus, the graph of $h$ must contain the points $(3, 1)$ and $(9, 2)$.
Checking the options, $(3, 1)$ and $(9, 2)$ correspond to option (D).

Question

The figure shows a portion of the graph of a function $f$ that has the $x$-axis as a horizontal asymptote. The points $(1, 3)$, $(2, 9)$, and $(3, 27)$ are on the graph of $f$. Which of the following could be the inverse function of $f$, for $x > 0$?

(A) $f^{-1}(x) = \frac{1}{3^x}$

(B) $f^{-1}(x) = 3^x$

(D) $f^{-1}(x) = \log_3 x$

▶️ Answer/Explanation

Detailed solution

The correct option is (D).

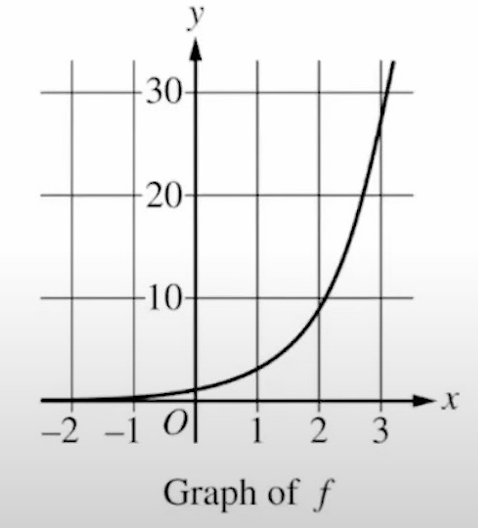
Step 1: Analyze the given points on the graph to identify the function $f(x)$. The points are $(1, 3)$, $(2, 9)$, and $(3, 27)$.

Step 2: Observe the exponential pattern: $3^1 = 3$, $3^2 = 9$, and $3^3 = 27$. This indicates that the function is $f(x) = 3^x$. This function has the $x$-axis as a horizontal asymptote.

Step 3: To find the inverse function, let $y = f(x)$, so we have $y = 3^x$.

Step 4: Interchange the variables $x$ and $y$ to solve for the inverse: $x = 3^y$.

Step 5: Convert the exponential equation into logarithmic form. By definition, $x = 3^y$ is equivalent to $y = \log_3 x$.

Step 6: Therefore, the inverse function is $f^{-1}(x) = \log_3 x$.

Question

The figure shows the graph of an exponential function $k$, where $k(x) = b^x$ for $b > 0$ and $b \neq 1$. Consider the logarithmic function $h$ (not shown) given by $h(x) = \log_b x$. Of the following pairs of points, which are on the graph of $h$?

(A) $(-3, -1)$ and $(-9, -2)$

(B) $(1, \frac{1}{3})$ and $(2, \frac{1}{9})$

(D) $(3, 1)$ and $(9, 2)$

▶️ Answer/Explanation

Detailed solution

The correct option is (D).

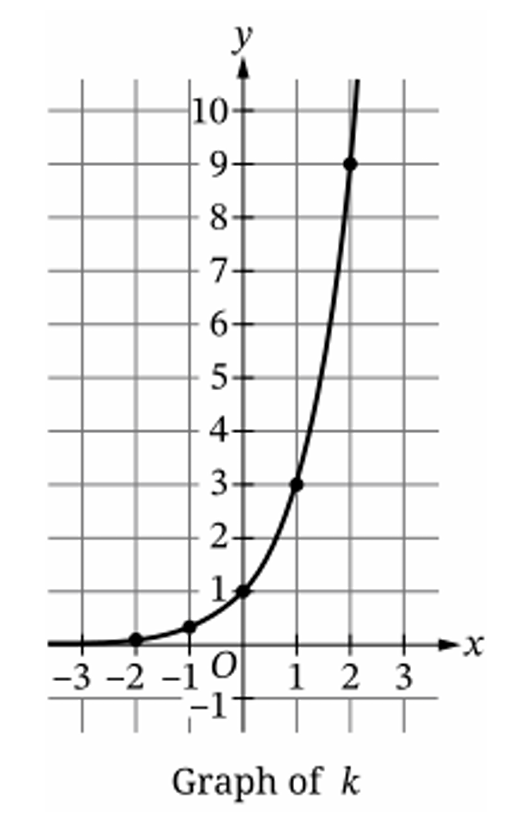
1. First, identify the base $b$ using a clear point on the graph of $k(x)$. The graph passes through the point $(1, 3)$.
2. Substitute these coordinates into the exponential equation $y = b^x$: $3 = b^1$, which implies $b = 3$.
3. The logarithmic function $h(x) = \log_b x$ is the inverse of the exponential function $k(x) = b^x$.
4. Since they are inverse functions, if a point $(x, y)$ lies on the graph of $k$, then the point $(y, x)$ must lie on the graph of $h$.
5. From the graph of $k$, we can identify the points $(1, 3)$ and $(2, 9)$ because $3^1 = 3$ and $3^2 = 9$.
6. Swapping the coordinates for the inverse function $h$, the corresponding points are $(3, 1)$ and $(9, 2)$.
7. Checking option (D): $h(3) = \log_3(3) = 1$ and $h(9) = \log_3(9) = 2$. These matches the points derived.

Question

The function $f$ is given by $f(x) = 4 \cdot 2^{(x-3)}$. If the function $g$ is the inverse of $f$, which of the following could define $g(x)$?

(A) $\log_{8} x + 3$
(B) $\log_{2}(4x) + 3$
(C) $\log_{2}\left(\frac{x}{4}\right) + 3$
(D) $\log_{2}\left(\frac{x-3}{4}\right)$

▶️ Answer/Explanation

Detailed solution

Set $y = 4 \cdot 2^{(x-3)}$ to represent the original function.
To find the inverse, swap $x$ and $y$: $x = 4 \cdot 2^{(y-3)}$.
Divide both sides by $4$: $\frac{x}{4} = 2^{(y-3)}$.
Convert the exponential equation to logarithmic form: $\log_{2}\left(\frac{x}{4}\right) = y – 3$.
Solve for $y$ by adding $3$ to both sides: $y = \log_{2}\left(\frac{x}{4}\right) + 3$.
Therefore, $g(x) = \log_{2}\left(\frac{x}{4}\right) + 3$.
The correct option is (C).

Question

The function $f$ is given by $f(x) = \log_2(\log_3 x)$. Which of the following is an expression for $f^{-1}(x)$ ?

(A) $2^{(3^x)}$

(B) $3^{(2^x)}$

(D) $3 \cdot 2^x$

▶️ Answer/Explanation

Detailed solution

Set $y = \log_2(\log_3 x)$ to begin the inversion process.
Apply the base-2 exponential to both sides: $2^y = \log_3 x$.
Apply the base-3 exponential to isolate $x$: $3^{(2^y)} = x$.
Interchange $x$ and $y$ to find the inverse function.
The resulting expression is $f^{-1}(x) = 3^{(2^x)}$.
Therefore, the correct choice is (B).

Question

The exponential function $g$ is given by $g(x) = 5^{x}$. Which of the following expressions defines $g^{-1}(x)$?

(A) $\log_{5} x$

(B) $\log_{x} 5$

(D) $\sqrt[x]{5}$

▶️ Answer/Explanation

Detailed solution

To find the inverse $g^{-1}(x)$, start by setting $y = 5^{x}$.
Switch the variables $x$ and $y$ to get $x = 5^{y}$.
Solve for $y$ by converting the exponential equation to logarithmic form.
The definition of a logarithm states that if $x = b^{y}$, then $y = \log_{b} x$.
Applying this here, we get $y = \log_{5} x$.
Therefore, $g^{-1}(x) = \log_{5} x$.
The correct option is (A).

Question

The function $f$ is given by $f(x) = \log_{3} x$. Which of the following could be the graph of $y = f^{-1}(x)$?

(A)

(B)

(C)

(D)

▶️ Answer/Explanation

Detailed solution

The inverse of the logarithmic function $f(x) = \log_{3} x$ is found by switching $x$ and $y$, resulting in $y = 3^x$.
The graph of $y = 3^x$ must be an exponential growth curve that stays strictly above the $x$-axis.
The $y$-intercept occurs at $(0, 1)$ since $3^0 = 1$.
The graph must pass through the point $(1, 3)$ since $3^1 = 3$.
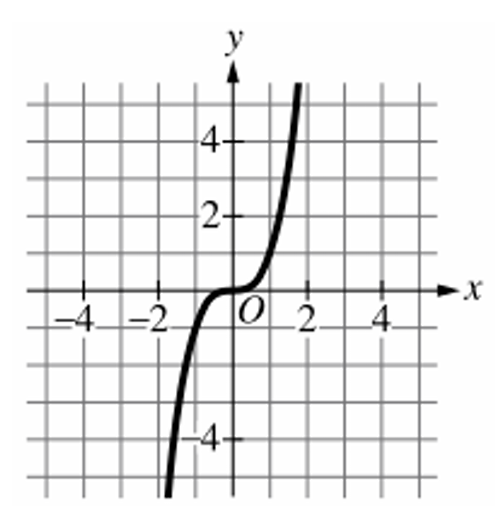
Graph B passes through $(0, 1)$ but appears to pass through $(1, 2)$, suggesting the function $y = 2^x$.
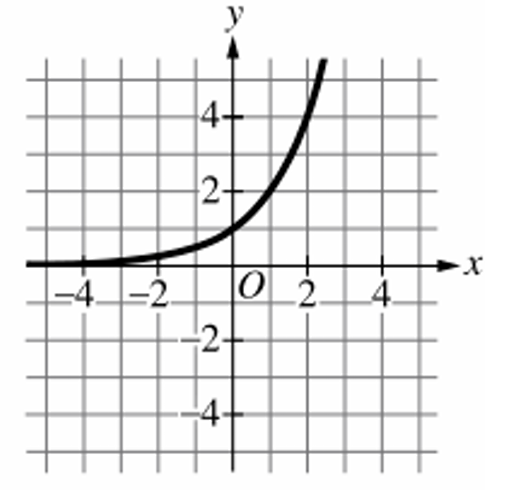
Graph C passes through $(0, 1)$ and reaches $y = 3$ when $x = 1$, matching the function $y = 3^x$.
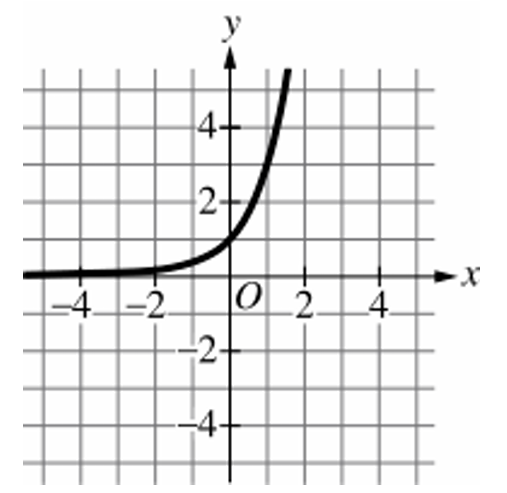
Graph A represents a cubic-style function, and Graph D shows a reciprocal-style function.
Therefore, the correct choice is (C).

Question

Which of the following is the inverse of the function $f$ given by $f(x) = 4 \log_{2}(x + 3) – 1$?

(A) $g(x) = \frac{1}{4}(2^{x} + 1) – 3$

(B) $g(x) = \frac{1}{4} \cdot 2^{(x+1)} – 3$

(D) $g(x) = 2^{(\frac{x+1}{4})} – 3$

▶️ Answer/Explanation

Detailed solution

Set $y = 4 \log_{2}(x + 3) – 1$ and swap $x$ and $y$ to find the inverse.
$x = 4 \log_{2}(y + 3) – 1$
Add $1$ to both sides: $x + 1 = 4 \log_{2}(y + 3)$
Divide by $4$: $\frac{x + 1}{4} = \log_{2}(y + 3)$
Rewrite in exponential form: $2^{(\frac{x + 1}{4})} = y + 3$
Subtract $3$ to isolate $y$: $y = 2^{(\frac{x + 1}{4})} – 3$
The inverse function is $g(x) = 2^{(\frac{x + 1}{4})} – 3$, which matches option (D).

Question

The function $f$ is given by $f(x) = \log_{2} x$. What input value in the domain of $f$ yields an output value of $4$ ?

(A) $32$

(B) $16$

(D) $\frac{1}{2}$

▶️ Answer/Explanation

Detailed solution

The given function is $f(x) = \log_{2} x$.
The problem asks for the input $x$ such that the output $f(x) = 4$.
Substitute the output value into the function: $\log_{2} x = 4$.
Convert the logarithmic form to exponential form using the rule: $\log_{b} a = c \Rightarrow b^{c} = a$.
This yields the equation $x = 2^{4}$.
Calculate the value of the exponent: $2 \times 2 \times 2 \times 2 = 16$.
Therefore, the input value is $16$, which corresponds to option (B).

Question

Directions:

Unless otherwise specified, the domain of a function $ f $ is assumed to be the set of all real numbers $ x $ for which $ f(x) $ is a real number. Angle measures for trigonometric functions are assumed to be in radians.
Solutions to equations must be real numbers. Determine the exact value of any expression that can be obtained without a calculator. For example, $ \log_2 8 $, $ \cos(\frac{\pi}{2}) $, and $ \sin^{-1}(1) $ can be evaluated without a calculator.
Unless otherwise specified, combine terms using algebraic methods and rules for exponents and logarithms, where applicable. For example, $ 2x + 3x $, $ 5^2 \cdot 5^3 $, $ \frac{x^5}{x^2} $, and $ \ln 3 + \ln 5 $ should be rewritten in equivalent forms.
For each part of the question, show the work that leads to your answers.

Part A
The functions $ g $ and $ h $ are given by

$ g(x) = \log_5(4x – 2) $
$ h(x) = \sin^{-1}(8x) $

(i) Solve $ g(x) = 3 $ for values of $ x $ in the domain of $ g $.

(ii) Solve $ h(x) = \frac{\pi}{4} $ for values of $ x $ in the domain of $ h $.

Part B
The functions $ j $ and $ k $ are given by

$ j(x) = (\sec x)(\cot x) $
$ k(x) = \frac{(16^{3x}) \cdot 4^x}{2} $

(i) Rewrite $ j(x) $ as an expression involving $ \sin x $ and no other trigonometric functions.

(ii) Rewrite $ k(x) $ as an expression of the form $ 4^{(ax+b)} $, where $ a $ and $ b $ are constants.

Part C
The function $ m $ is given by

$ m(x) = \sqrt{3}\tan(x + \frac{\pi}{2}) $.

Find all values in the domain of $ m $ that yield an output value of 1.

▶️ Answer/Explanation

Detailed solution

Part A
(i) Solve $ g(x) = 3 $
Start with the given equation:
$ \log_5(4x – 2) = 3 $
Convert the logarithmic equation to exponential form ($ y = \log_b x \iff x = b^y $):
$ 4x – 2 = 5^3 $
Evaluate the exponent:
$ 4x – 2 = 125 $
Add 2 to both sides:
$ 4x = 127 $
Divide by 4:
$ x = \frac{127}{4} $

(ii) Solve $ h(x) = \frac{\pi}{4} $
Start with the given equation:
$ \sin^{-1}(8x) = \frac{\pi}{4} $
Take the sine of both sides to isolate the argument:
$ 8x = \sin\left(\frac{\pi}{4}\right) $
Substitute the exact value of $ \sin\left(\frac{\pi}{4}\right) $:
$ 8x = \frac{\sqrt{2}}{2} $
Divide by 8:
$ x = \frac{\sqrt{2}}{16} $

Part B
(i) Rewrite $ j(x) $
Start with the function definition:
$ j(x) = (\sec x)(\cot x) $
Substitute the reciprocal and quotient identities ($ \sec x = \frac{1}{\cos x} $ and $ \cot x = \frac{\cos x}{\sin x} $):
$ j(x) = \left(\frac{1}{\cos x}\right) \left(\frac{\cos x}{\sin x}\right) $
Cancel the $ \cos x $ terms:
$ j(x) = \frac{1}{\sin x} $

(ii) Rewrite $ k(x) $
Start with the function definition:
$ k(x) = \frac{(16^{3x}) \cdot 4^x}{2} $
To write in the form $ 4^{(ax+b)} $, convert bases 16 and 2 to base 4.
Since $ 16 = 4^2 $ and $ 2 = \sqrt{4} = 4^{1/2} = 4^{0.5} $:
$ k(x) = \frac{(4^2)^{3x} \cdot 4^x}{4^{0.5}} $
Apply the power of a power rule ($ (a^m)^n = a^{mn} $):
$ k(x) = \frac{4^{6x} \cdot 4^x}{4^{0.5}} $
Apply the product rule for exponents ($ a^m \cdot a^n = a^{m+n} $) in the numerator:
$ k(x) = \frac{4^{6x + x}}{4^{0.5}} = \frac{4^{7x}}{4^{0.5}} $
Apply the quotient rule for exponents ($ \frac{a^m}{a^n} = a^{m-n} $):
$ k(x) = 4^{7x – 0.5} $ (or $ 4^{7x – \frac{1}{2}} $)
Thus, $ a = 7 $ and $ b = -0.5 $.

Part C
Find values where $ m(x) = 1 $
Set the function equal to 1:
$ \sqrt{3}\tan\left(x + \frac{\pi}{2}\right) = 1 $
Isolate the tangent function by dividing by $ \sqrt{3} $:
$ \tan\left(x + \frac{\pi}{2}\right) = \frac{1}{\sqrt{3}} $
Determine the reference angle. We know that $ \tan\left(\frac{\pi}{6}\right) = \frac{1}{\sqrt{3}} $.
Set up the general solution for tangent ($ \theta = \text{ref} + n\pi $):
$ x + \frac{\pi}{2} = \frac{\pi}{6} + n\pi $, where $ n $ is any integer.
Solve for $ x $ by subtracting $ \frac{\pi}{2} $ from both sides:
$ x = \frac{\pi}{6} – \frac{\pi}{2} + n\pi $
Find a common denominator (6) to combine fractions:
$ x = \frac{\pi}{6} – \frac{3\pi}{6} + n\pi $
$ x = -\frac{2\pi}{6} + n\pi $
Simplify the fraction:
$ x = -\frac{\pi}{3} + n\pi $

AP Precalculus -2.10 Inverses of Exponential Functions- MCQ Exam Style Questions - Effective Fall 2023