AP Precalculus -2.10 Inverses of Exponential Functions- Study Notes - Effective Fall 2023
AP Precalculus -2.10 Inverses of Exponential Functions- Study Notes – Effective Fall 2023
AP Precalculus -2.10 Inverses of Exponential Functions- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Construct representations of the inverse of an exponential function with an initial value of 1.
Key Concepts:
General Form of a Logarithmic Function
Inverse Relationship Between Exponential and Logarithmic Functions
Exponential and Logarithmic Functions as Inverses
Graphical Relationship Between Exponential and Logarithmic Functions
Ordered Pairs of Exponential and Logarithmic Functions
General Form of a Logarithmic Function
The general form of a logarithmic function is
\( \mathrm{ \displaystyle f(x) = a \log_b x } \)
where:
• \( \mathrm{b>0} \)
• \( \mathrm{b \ne 1} \)
• \( \mathrm{a \ne 0} \)
Logarithmic functions are the inverse functions of exponential functions. The logarithm answers the question: to what power must the base \( \mathrm{b} \) be raised to obtain \( \mathrm{x} \).
The constant \( \mathrm{a} \) controls a vertical dilation of the graph and may also cause a reflection across the x-axis if \( \mathrm{a<0} \).
Key Properties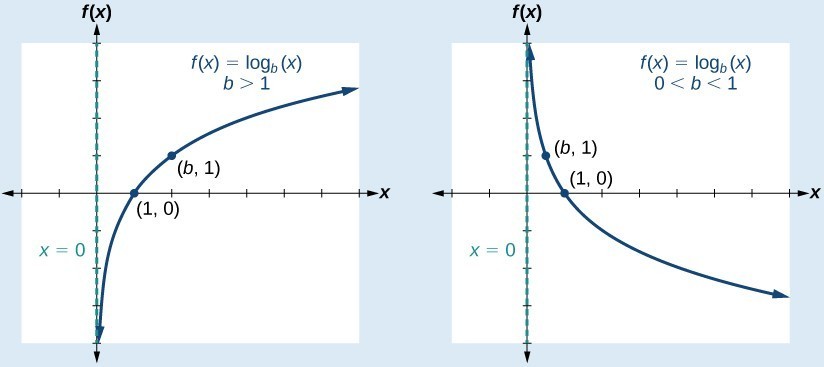
• Domain: \( \mathrm{x>0} \)
• Range: all real numbers
• Vertical asymptote: \( \mathrm{x=0} \)
If \( \mathrm{b>1} \), the function is increasing. If \( \mathrm{0<b<1} \), the function is decreasing.
Example
Consider the function
\( \mathrm{ \displaystyle f(x) = 2\log_{10} x } \)
State the base, describe the effect of the coefficient, and give the domain.
▶️ Answer/Explanation
The base is \( \mathrm{10} \).
The coefficient \( \mathrm{2} \) causes a vertical stretch by a factor of 2.
Since logarithms are only defined for positive inputs, the domain is
\( \mathrm{ \displaystyle x>0 } \)
Example
Consider the function
\( \mathrm{ \displaystyle f(x) = -\log_2 x } \)
Describe how this function compares to \( \mathrm{y=\log_2 x} \).
▶️ Answer/Explanation
The coefficient \( \mathrm{-1} \) reflects the graph across the x-axis.
The base is \( \mathrm{2} \), so the function would normally be increasing, but the reflection makes it decreasing.
The domain remains
\( \mathrm{ \displaystyle x>0 } \)
Inverse Relationship Between Exponential and Logarithmic Functions
Exponential and logarithmic functions have an inverse relationship in the way their input and output values vary together.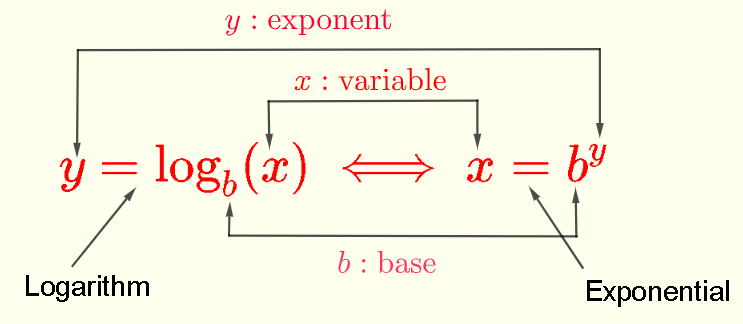
For a general-form exponential function, equal increases in the input variable result in proportional (multiplicative) changes in the output values.
\( \mathrm{ \displaystyle f(x) = ab^x } \)
In contrast, for a general-form logarithmic function, equal increases in the output values correspond to proportional (multiplicative) changes in the input values.
\( \mathrm{ \displaystyle g(x) = a\log_b x } \)
This inverse behavior can also be described as follows:
• Exponential growth: output values change multiplicatively as input values change additively
• Logarithmic growth: output values change additively as input values change multiplicatively
Because logarithmic functions are the inverses of exponential functions, they reverse this pattern of change.
Example
Consider the exponential function
\( \mathrm{ \displaystyle f(x) = 2^x } \)
Describe how the output values change as the input increases by 1.
▶️ Answer/Explanation
Each increase of 1 in the input multiplies the output by 2:
\( \mathrm{ \displaystyle \dfrac{f(x+1)}{f(x)} = \dfrac{2^{x+1}}{2^x} = 2 } \)
Conclusion
The output values change multiplicatively while the input changes additively, which is characteristic of exponential growth.
Example
Consider the logarithmic function
\( \mathrm{ \displaystyle g(x) = \log_{2} x } \)
Describe how the input values change when the output increases by 1.
▶️ Answer/Explanation
An increase of 1 in the output corresponds to doubling the input:
\( \mathrm{ \displaystyle g(2x) = \log_2(2x) = \log_2 x + 1 } \)
Conclusion
The output changes additively while the input changes multiplicatively, which is characteristic of logarithmic growth.
Exponential and Logarithmic Functions as Inverses
Exponential and logarithmic functions with the same base are inverse functions of each other.
If
\( \mathrm{ \displaystyle f(x) = \log_b x } \)
and
\( \mathrm{ \displaystyle g(x) = b^x } \)
where \( \mathrm{b>0} \) and \( \mathrm{b \ne 1} \), then \( \mathrm{f} \) and \( \mathrm{g} \) are inverses.
This means that composing one with the other returns the input value:
\( \mathrm{ \displaystyle g(f(x)) = b^{\log_b x} = x } \)
and
\( \mathrm{ \displaystyle f(g(x)) = \log_b(b^x) = x } \)
This inverse relationship explains why logarithms are used to undo exponentiation and vice versa.
Key Consequences
• The domain of \( \mathrm{f(x)=\log_b x} \) is \( \mathrm{x>0} \)
• The range of \( \mathrm{f} \) is all real numbers
• The domain and range of \( \mathrm{g(x)=b^x} \) are reversed
Example
Let
\( \mathrm{ \displaystyle f(x) = \log_3 x \quad \text{and} \quad g(x) = 3^x } \)
Verify that \( \mathrm{f} \) and \( \mathrm{g} \) are inverse functions.
▶️ Answer/Explanation
Compute the compositions:
\( \mathrm{ \displaystyle g(f(x)) = 3^{\log_3 x} = x } \)
\( \mathrm{ \displaystyle f(g(x)) = \log_3(3^x) = x } \)
Conclusion
Since both compositions equal \( \mathrm{x} \), the functions are inverses.
Example
Evaluate the expression
\( \mathrm{ \displaystyle \log_5(5^7) } \)
▶️ Answer/Explanation
Since logarithmic and exponential functions with the same base are inverses:
\( \mathrm{ \displaystyle \log_5(5^7) = 7 } \)
Conclusion
The logarithm cancels the exponentiation, leaving the exponent.
Graphical Relationship Between Exponential and Logarithmic Functions
The graph of the logarithmic function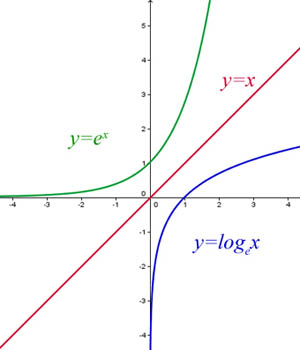
\( \mathrm{ \displaystyle f(x)=\log_b x } \)
where \( \mathrm{b>0} \) and \( \mathrm{b\ne1} \), is a reflection of the graph of the exponential function
\( \mathrm{ \displaystyle g(x)=b^x } \)
over the graph of the identity function
\( \mathrm{ \displaystyle h(x)=x } \)
This reflection occurs because logarithmic and exponential functions with the same base are inverse functions.
As a result:
• Points \( \mathrm{(a,b)} \) on \( \mathrm{y=b^x} \) correspond to points \( \mathrm{(b,a)} \) on \( \mathrm{y=\log_b x} \)
• The domain and range of the two functions are interchanged
• The vertical asymptote \( \mathrm{x=0} \) of the logarithmic function corresponds to the horizontal asymptote \( \mathrm{y=0} \) of the exponential function
This symmetry visually represents the inverse relationship between exponentiation and logarithms.
Example
Consider the exponential function
\( \mathrm{ \displaystyle g(x)=2^x } \)
A point on this graph is \( \mathrm{(3,8)} \).
Find the corresponding point on the graph of the logarithmic function.
▶️ Answer/Explanation
Swap the coordinates to reflect across \( \mathrm{y=x} \):
\( \mathrm{ \displaystyle (8,3) } \)
This point lies on the graph of
\( \mathrm{ \displaystyle f(x)=\log_2 x } \)
Example
Explain how the asymptotes of \( \mathrm{y=10^x} \) and \( \mathrm{y=\log_{10}x} \) are related.
▶️ Answer/Explanation
The exponential function has a horizontal asymptote at
\( \mathrm{ \displaystyle y=0 } \)
The logarithmic function has a vertical asymptote at
\( \mathrm{ \displaystyle x=0 } \)
Conclusion
These asymptotes are reflections of each other across the line \( \mathrm{y=x} \).
Ordered Pairs of Exponential and Logarithmic Functions
Exponential and logarithmic functions with the same base are inverse functions. Because of this inverse relationship, their ordered pairs are reversed.
If an ordered pair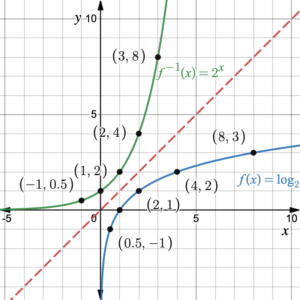
\( \mathrm{ \displaystyle (s,t) } \)
lies on the graph of the exponential function
\( \mathrm{ \displaystyle g(x)=b^x } \)
where \( \mathrm{b>0} \) and \( \mathrm{b\ne1} \), then the ordered pair
\( \mathrm{ \displaystyle (t,s) } \)
lies on the graph of the logarithmic function
\( \mathrm{ \displaystyle f(x)=\log_b x } \)
This reversal of coordinates occurs because the graphs of inverse functions are reflections of each other across the line
\( \mathrm{ \displaystyle y=x } \)
Key Idea
• Exponential point \( \mathrm{(x,b^x)} \) corresponds to logarithmic point \( \mathrm{(b^x,x)} \)
• Input and output values are interchanged
Example
A point on the graph of the exponential function
\( \mathrm{ \displaystyle g(x)=3^x } \)
is \( \mathrm{(2,9)} \). Find the corresponding point on the logarithmic function.
▶️ Answer/Explanation
Reverse the coordinates:
\( \mathrm{ \displaystyle (9,2) } \)
This point lies on the graph of
\( \mathrm{ \displaystyle f(x)=\log_3 x } \)
Example
Verify the relationship using a logarithmic value.
Suppose \( \mathrm{\log_5 25 = 2} \).
▶️ Answer/Explanation
This means the point
\( \mathrm{ \displaystyle (25,2) } \)
lies on \( \mathrm{y=\log_5 x} \).
Reversing the coordinates gives
\( \mathrm{ \displaystyle (2,25) } \)
which lies on the graph of the exponential function
\( \mathrm{ \displaystyle y=5^x } \)
