AP Precalculus -2.11 Logarithmic Functions- MCQ Exam Style Questions - Effective Fall 2023

AP Precalculus -2.11 Logarithmic Functions- MCQ Exam Style Questions – Effective Fall 2023

AP Precalculus -2.11 Logarithmic Functions- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.

AP Precalculus – MCQ Exam Style Questions- All Topics

Question

The function $ f $ is given by $ f(x) = \log_3 x $. Which of the following could be the graph of $ y = f^{-1}(x) $?

▶️ Answer/Explanation

Detailed solution

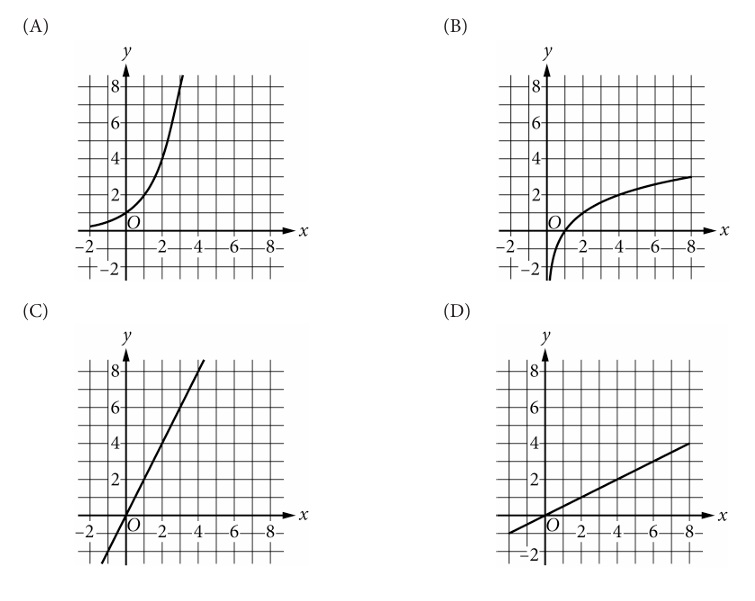
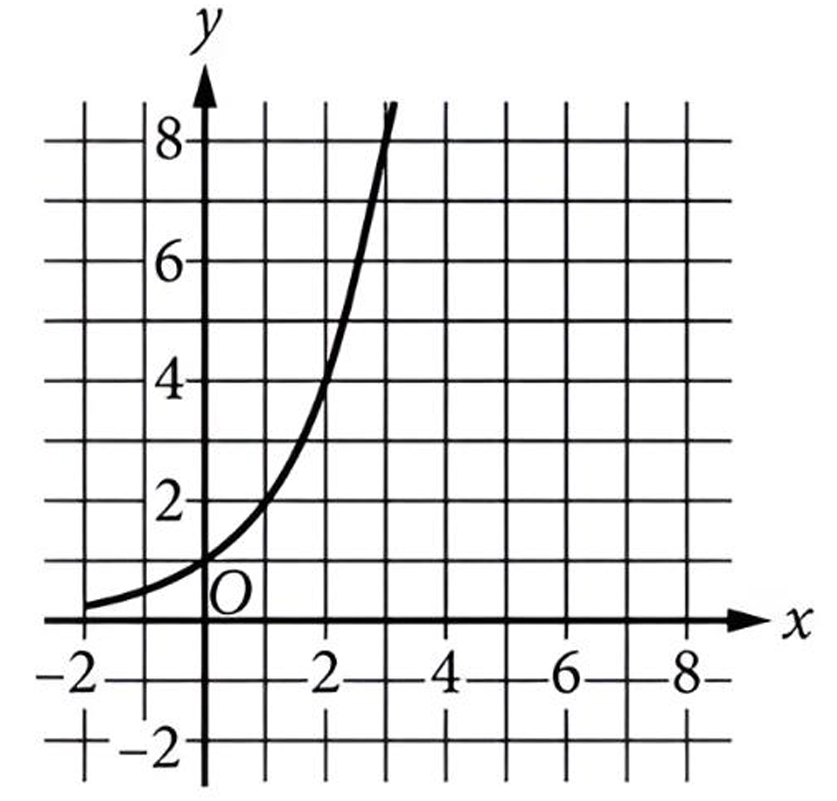
$ f^{-1}(x) = 3^x $, which is an exponential function with base >1.
It passes through (0,1), increases, and has a horizontal asymptote at $ y=0 $ as $ x \to -\infty $.
Only one of the graphs matches this exponential shape.
✅ Answer: (C)

Question

The function $ f $ is an increasing function such that every time the output values of the function $ f $ increase by 1, the corresponding input values multiply by 4. Which of the following could define $ f(x) $?

(A) $ x^4 $
(B) $ 4^x $
(C) $ \sqrt[4]{x} $
(D) $ \log_4 x $

▶️ Answer/Explanation

Detailed solution

If output increases by 1 when input multiplies by 4, then $ f(4x) = f(x) + 1 $.
This is a property of logarithmic functions: $ \log_b(kx) = \log_b k + \log_b x $.
With $ b=4 $, $ \log_4(4x) = \log_4 4 + \log_4 x = 1 + \log_4 x $.
✅ Answer: (D)

Question

The function $ f $ is given by $ f(x) = 2 \log_5 x $. Which of the following describes $ f $?

(A) $ f $ is an increasing function that increases at an increasing rate.
(B) $ f $ is an increasing function that increases at a decreasing rate.
(C) $ f $ is a decreasing function that decreases at an increasing rate.
(D) $ f $ is a decreasing function that decreases at a decreasing rate.

▶️ Answer/Explanation

Detailed solution

$ f(x) = 2 \log_5 x $ is a logarithmic function with base >1, so it is increasing.
Derivative $ f'(x) = \frac{2}{x \ln 5} $ which is positive but decreasing as $ x $ increases, so rate of increase slows down.
Graph is concave down ⇒ increases at a decreasing rate.
✅ Answer: (B)

Question

Which of the following could describe a single logarithmic function $ f $?

(A) $ \lim_{x \to 0^+} f(x) = -\infty $ and $ \lim_{x \to \infty} f(x) = -\infty $
(B) $ \lim_{x \to 0^+} f(x) = -\infty $ and $ \lim_{x \to \infty} f(x) = k $, where $ k $ is a positive constant
(C) $ \lim_{x \to 0^+} f(x) = \infty $ and $ \lim_{x \to \infty} f(x) = 0 $
(D) $ \lim_{x \to 0^+} f(x) = \infty $ and $ \lim_{x \to \infty} f(x) = -\infty $

▶️ Answer/Explanation

Detailed solution

Typical log function $ \log_b x $ with $ b>1 $ satisfies $ \lim_{x \to 0^+} = -\infty $, $ \lim_{x \to \infty} = \infty $.
But if we take $ f(x) = -\log_b x $ (still logarithmic), then $ \lim_{x \to 0^+} = \infty $, $ \lim_{x \to \infty} = -\infty $.
This matches (D).
✅ Answer: (D)

Question

The logarithmic function $ f $ is defined by $ f(x) = \log_3 x $ on a domain of $ 0 < x \leq 9 $. Which of the following is true of $ f $?

(A) $ f $ has both a maximum and a minimum value.
(B) $ f $ has a maximum value, but no minimum value.
(C) $ f $ has a minimum value, but no maximum value.
(D) $ f $ has neither a minimum value nor a maximum value.

▶️ Answer/Explanation

Detailed solution

$ f $ is increasing on $ (0, 9] $.
As $ x \to 0^+ $, $ f(x) \to -\infty $, so no minimum.
At $ x = 9 $, $ f(9) = \log_3 9 = 2 $, which is the maximum on the closed interval at the right endpoint.
✅ Answer: (B)

Question

The function $ f $ is given by $ f(x) = \ln x $. Which of the following describes input values for which the output values of $ f $ are integers?

(A) Integer powers of $ e $
(B) Integer powers of 10
(C) Integers raised to the power $ e $
(D) Integers raised to the power 10

▶️ Answer/Explanation

Detailed solution

The natural logarithm $ \ln x $ is the logarithm with base $ e $, so $ \ln(e^k) = k $ for any real number $ k $.
If $ k $ is an integer, then $ \ln(e^k) $ is an integer.
Therefore, input values that are integer powers of $ e $ produce integer outputs.
✅ Answer: (A)

Question

The function $ f $ is logarithmic, and the points $ (2,1) $ and $ (4,2) $ are on the graph of $ f $ in the $ xy $-plane. Which of the following could define $ f(x) $?

(A) $ \log_4 x $
(B) $ 2\log_2 x $
(C) $ 2\log_4 x $
(D) $ \log_4(x + 2) $

▶️ Answer/Explanation

Detailed solution

Check each option against the two given points $ (2,1) $ and $ (4,2) $.
(C) $ f(x) = 2 \log_4 x $:
For $ x = 2 $: $ f(2) = 2 \log_4 2 = 2 \cdot \frac{1}{2} = 1 $ ✅
For $ x = 4 $: $ f(4) = 2 \log_4 4 = 2 \cdot 1 = 2 $ ✅
Both points satisfy the equation.
✅ Answer: (C)

Question

The function $ g $ has the property that for each time the input values double, the output values increase by 1. Which of the following could be the graph of $ y = g(x) $ in the $ xy $-plane?

▶️ Answer/Explanation

Detailed solution

The property describes logarithmic behavior:
If input doubles ($ x \to 2x $), output increases by 1 ($ g(2x) = g(x) + 1 $).
This matches $ g(x) = \log_2 x $ because:
\[ \log_2(2x) = \log_2 2 + \log_2 x = 1 + \log_2 x = 1 + g(x) \]
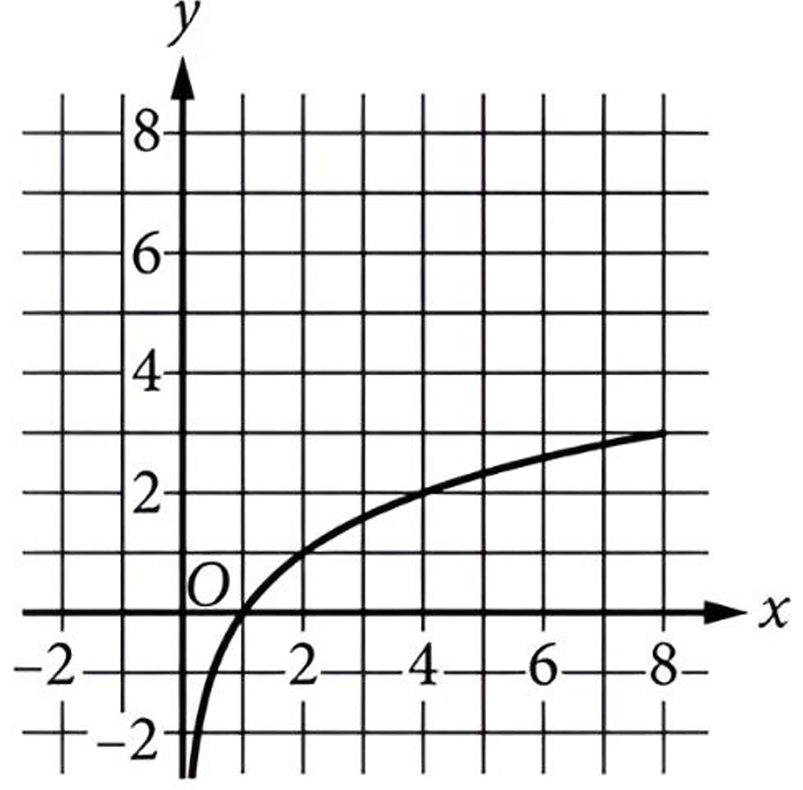
So $ g $ is logarithmic, with a slowly increasing curve, domain $ x > 0 $, and passes through $(1,0)$, $(2,1)$, $(4,2)$, etc.

✅ Answer: (B)

Question

Which one of the following logarithmic equations has a vertical asymptote of $\lim_{x \to 2^-} f(x) = \infty$?

a. $y = -\log(-x – 2) + 3$

b. $y = -2 \log(-2x + 4) – 2$

c. $y = -\log(x – 2)$

d. $y = \log(-(x – 2)) + 1$

▶️ Answer/Explanation

Detailed solution

The correct option is d.
The limit $\lim_{x \to 2^-} f(x) = \infty$ requires the function to be defined for $x < 2$.
In option (d), the argument is $-(x – 2)$, which is positive when $x < 2$.
As $x$ approaches $2$ from the left ($2^-$), the argument $-(x – 2)$ approaches $0^+$.
The basic property of logarithms is that $\lim_{u \to 0^+} \log(u) = -\infty$.
However, we need the limit to be $+\infty$, which usually requires a reflection.

Question

Consider the functions $ f $ and $ g $ given by $ f(x) = \ln(-x + 8) $ and $ g(x) = \ln(x + 2) + \ln(x – 8) $. In the $ xy $-plane, what are all the $ x $-coordinates of the points of intersection of the graphs $ f $ and $ g $?

(A) $ x = 8 $

(B) $ x = -3 $

(D) No Solution

▶️ Answer/Explanation

Detailed solution

To find the intersection, we must ensure $ x $ exists in the domains of both functions.
First, for $ f(x) = \ln(-x + 8) $, the argument must be positive: $ -x + 8 > 0 \Rightarrow x < 8 $.
Second, for $ g(x) = \ln(x + 2) + \ln(x – 8) $, both arguments must be positive.
This requires $ x > -2 $ and $ x > 8 $. The combined condition for $ g(x) $ is $ x > 8 $.
Comparing the domains, $ f(x) $ requires $ x < 8 $ while $ g(x) $ requires $ x > 8 $.
Since no real number is simultaneously less than 8 and greater than 8, the domains do not overlap.
Therefore, there are no points of intersection. (Note: $ x=-3 $ is an extraneous algebraic solution).

Question

The function $ g $ has the property that for each time the input values double, the output values increase by 1. Which of the following could be the graph of $ g(x) $ in the $ xy $-plane?

(A)

(B)

(C)

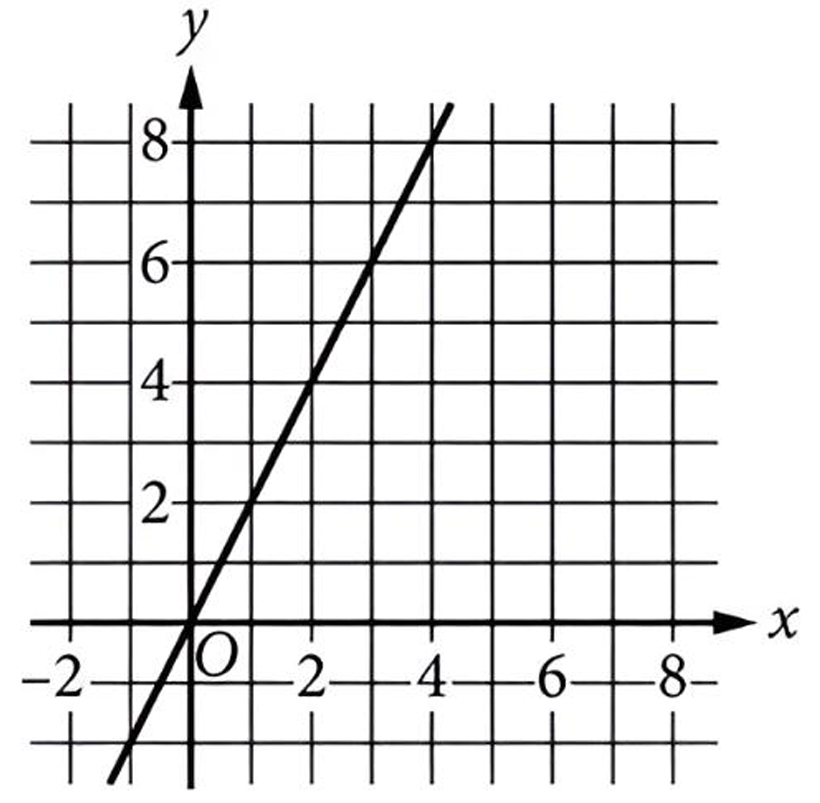
(D)

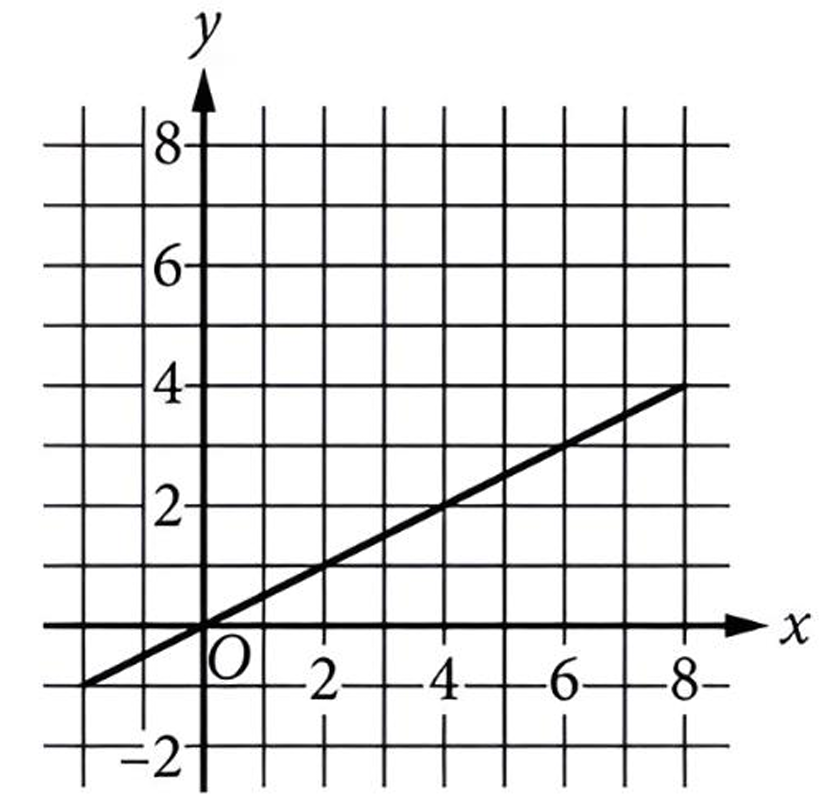
▶️ Answer/Explanation

Detailed solution

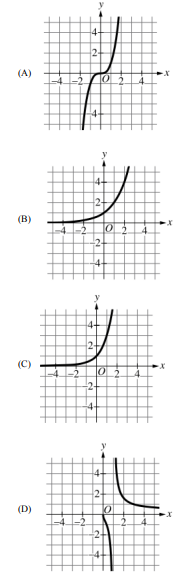
The problem describes a function property: when input $ x $ doubles ($ x \rightarrow 2x $), the output increases by 1 ($ g(x) \rightarrow g(x) + 1 $).
This relationship is written as $ g(2x) = g(x) + 1 $, which is characteristic of a logarithmic function $ g(x) = \log_2(x) $.
Let’s test the points on Graph (B) to verify this:
• At $ x = 1 $, $ y = 0 $.
• At $ x = 2 $ (doubled), $ y = 1 $. The increase is $ 1 – 0 = 1 $.
• At $ x = 4 $ (doubled), $ y = 2 $. The increase is $ 2 – 1 = 1 $.
• At $ x = 8 $ (doubled), $ y = 3 $. The increase is $ 3 – 2 = 1 $.
Graphs (C) and (D) represent linear functions passing through the origin, where doubling input doubles the output.
Graph (A) represents an exponential function, which grows much faster than the required condition.
Therefore, Graph (B) is the correct answer.

Question

A logarithmic function $ g $ is created by transforming the function $ f(x) = \log_5(x) $ such that $ g(x) = \frac{1}{2}f(x+3) + 2 $. What is the value of $ g^{-1}(3) $?

(A) $ 55 $

(B) $ \sqrt{7} $

(D) $ 22 $

▶️ Answer/Explanation

Detailed solution

To find the value of $ g^{-1}(3) $, we need to find the value of $ x $ such that $ g(x) = 3 $.
First, substitute $ f(x) $ into the given equation for $ g(x) $:
$ g(x) = \frac{1}{2}\log_5(x+3) + 2 $
Set the equation equal to 3 and solve for $ x $:
$ \frac{1}{2}\log_5(x+3) + 2 = 3 $
Subtract 2 from both sides: $ \frac{1}{2}\log_5(x+3) = 1 $
Multiply both sides by 2: $ \log_5(x+3) = 2 $
Convert the logarithmic equation to exponential form: $ x + 3 = 5^2 $
Solve for $ x $: $ x = 25 – 3 = 22 $.
Therefore, the correct option is (D).

Question

A logarithmic function $ f(x) = 2 \log(x + h) + k $ has an end behavior of $ \lim_{x\to-3^+} f(x) = -\infty $ and passes through the point $ (-2, 4) $. Which of the following are the values for $ h $ and $ k $?

(A) $ h = 3 $ and $ k = 4 $

(B) $ h = 4 $ and $ k = 7 $

(D) $ h = 7 $ and $ k = 8 $

▶️ Answer/Explanation

Detailed solution

The correct option is (A).

The limit $ \lim_{x\to-3^+} f(x) = -\infty $ implies a vertical asymptote at $ x = -3 $.
For the logarithm to be undefined at this asymptote, the argument must be zero: $ x + h = 0 $.
Substituting $ x = -3 $, we get $ -3 + h = 0 $, so $ h = 3 $.
The function passes through $ (-2, 4) $, so substitute $ x = -2 $, $ f(x) = 4 $, and $ h = 3 $.
$ 4 = 2 \log(-2 + 3) + k \Rightarrow 4 = 2 \log(1) + k $.
Since $ \log(1) = 0 $, the equation becomes $ 4 = 0 + k $, which gives $ k = 4 $.

Question

Consider the constant function $ f $ given by $ f(x) = -1 $ and the function $ g $ given by $ g(x) = \log_3 x $. Let $ h $ be the function given by $ h(x) = g(x) – f(x) $. In the $ xy $-plane, what is the $ x $-intercept of the graph of $ h $?

(A) $ (-3, 0) $

(B) $ (\frac{1}{3}, 0) $

(D) The graph of $ h $ does not have an $ x $-intercept.

▶️ Answer/Explanation

Detailed solution

The correct option is (B).

First, determine the expression for $ h(x) $ by substituting $ f(x) $ and $ g(x) $.
Given $ h(x) = g(x) – f(x) $, we have $ h(x) = \log_3 x – (-1) $, which simplifies to $ h(x) = \log_3 x + 1 $.
To find the $ x $-intercept, we set the function equal to zero: $ h(x) = 0 $.
This gives the equation: $ \log_3 x + 1 = 0 $.
Isolate the logarithmic term by subtracting 1 from both sides: $ \log_3 x = -1 $.
Convert the logarithmic equation to exponential form ($ x = b^y $): $ x = 3^{-1} $.
Simplifying this yields $ x = \frac{1}{3} $.
Therefore, the $ x $-intercept is the coordinate $ (\frac{1}{3}, 0) $.

Question (Calc allowed)

The function $S$ is given by $S(t) = \frac{500,000}{1 + 0.4e^{kt}}$, where $k$ is a constant. If $S(4) = 300,000$, what is the value of $S(12)$?

(A) $175,325$
(B) $214,772$
(C) $343,764$
(D) $357,143$

▶️ Answer/Explanation

Detailed solution

Set up the equation $S(4) = 300,000$: $\frac{500,000}{1 + 0.4e^{4k}} = 300,000$.
Simplify to find $e^{4k}$: $1 + 0.4e^{4k} = \frac{500,000}{300,000} = \frac{5}{3}$.
Solve for the exponential term: $0.4e^{4k} = \frac{5}{3} – 1 = \frac{2}{3}$, so $e^{4k} = \frac{2/3}{0.4} = \frac{5}{3}$.
Express the target value $S(12)$ using $e^{4k}$: $S(12) = \frac{500,000}{1 + 0.4(e^{4k})^3}$.
Substitute $e^{4k} = \frac{5}{3}$ into the expression: $S(12) = \frac{500,000}{1 + 0.4(\frac{5}{3})^3}$.
Calculate the denominator: $1 + 0.4(\frac{125}{27}) = 1 + \frac{50}{27} = \frac{77}{27}$.
Final calculation: $S(12) = \frac{500,000 \times 27}{77} \approx 175,324.67$.
The correct option is (A).

Question

The function $g$ has the property that for each time the input values double, the output values increase by $1$. Which of the following could be the graph of $y = g(x)$ in the $xy$-plane?

(A)

(B)

(C)

(D)

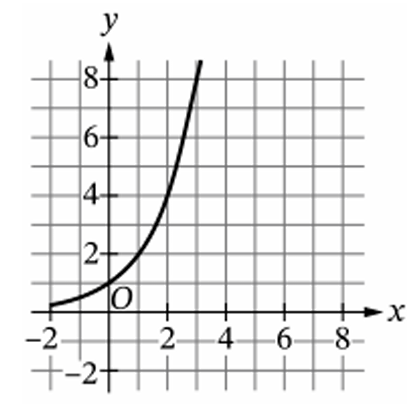
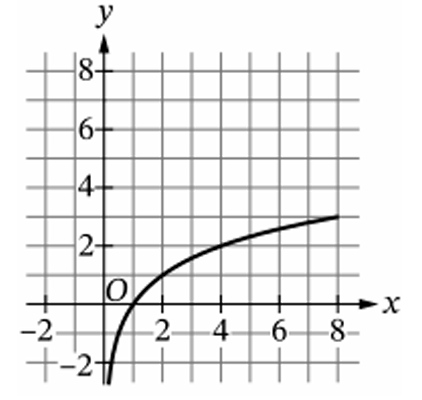
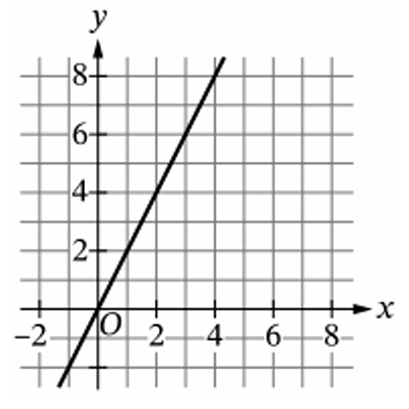
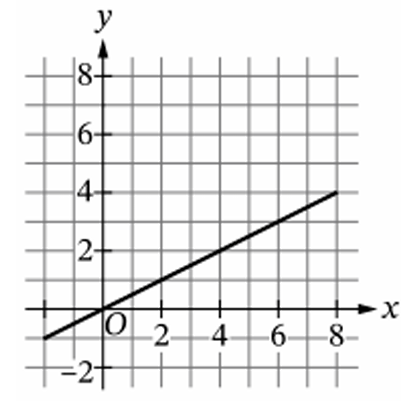
▶️ Answer/Explanation

Detailed solution

The given property $g(2x) = g(x) + 1$ defines a logarithmic function base $2$.
In graph (B), when the input $x$ is $1$, the output $y$ is $0$.
Doubling the input to $x = 2$ results in an output of $y = 1$ (an increase of $1$).
Doubling the input again to $x = 4$ results in an output of $y = 2$ (an increase of $1$).
Doubling the input once more to $x = 8$ results in an output of $y = 3$ (an increase of $1$).
This constant arithmetic increase for a geometric change in input is unique to logarithmic curves.
Graphs (C) and (D) are linear, where output increases by a constant amount for a constant addition to the input.
Graph (A) is exponential, which is the inverse relationship where input increases by $1$ as output doubles.
The correct choice is (B).

Question

The function $f$ is an increasing function such that every time the output values of the function $f$ increase by $1$, the corresponding input values multiply by $4$. Which of the following could define $f(x)$?

(A) $x^4$

(B) $4^x$

(D) $\log_{4} x$

▶️ Answer/Explanation

Detailed solution

The problem states that if $f(x) = y$, then $f(4x) = y + 1$.
This relationship is a characteristic property of logarithmic functions.
For $f(x) = \log_{4} x$, if the input is multiplied by $4$, we get $f(4x) = \log_{4}(4x)$.
Using log properties: $\log_{4}(4x) = \log_{4} 4 + \log_{4} x$.
Since $\log_{4} 4 = 1$, the expression becomes $1 + f(x)$.
This matches the condition that the output increases by $1$ when the input is multiplied by $4$.
Therefore, the correct option is (D).

Question

The function $f$ is given by $f(x) = 2 \log_{5} x$. Which of the following describes $f$?

(A) $f$ is an increasing function that increases at an increasing rate.

(B) $f$ is an increasing function that increases at a decreasing rate.

(D) $f$ is a decreasing function that decreases at a decreasing rate.

▶️ Answer/Explanation

Detailed solution

The function is $f(x) = 2 \log_{5} x$, where the base $5 > 1$, making $f$ an increasing function.
To find the rate of change, we calculate the first derivative: $f'(x) = \frac{2}{x \ln 5}$.
Since $f'(x) > 0$ for all $x > 0$, the function is strictly increasing.
To find the rate of that increase, we look at the second derivative: $f”(x) = -\frac{2}{x^2 \ln 5}$.
Since $f”(x) < 0$ for all $x > 0$, the graph is concave down, meaning the rate is decreasing.
Therefore, $f$ increases at a decreasing rate.
The correct option is (B).

Question

Which of the following could describe a single logarithmic function $f$?

(A) $\lim_{x \to 0^+} f(x) = -\infty$ and $\lim_{x \to \infty} f(x) = -\infty$

(B) $\lim_{x \to 0^+} f(x) = -\infty$ and $\lim_{x \to \infty} f(x) = k$, where $k$ is a positive constant

(D) $\lim_{x \to 0^+} f(x) = \infty$ and $\lim_{x \to \infty} f(x) = -\infty$

▶️ Answer/Explanation

Detailed solution

A standard logarithmic function is $f(x) = \log_b(x)$.
If $0 < b < 1$, the function represents a logarithmic decay.
As $x$ approaches $0$ from the right, $\lim_{x \to 0^+} \log_b(x) = \infty$.
As $x$ increases toward infinity, $\lim_{x \to \infty} \log_b(x) = -\infty$.
This end behavior matches the conditions provided in option (D).
Other options fail because logs do not have horizontal asymptotes or return to $-\infty$.
Therefore, the correct description is given by choice (D).

Question

The logarithmic function $f$ is defined by $f(x) = \log_{3} x$ on a domain of $f$ is $0 < x \le 9$. Which of the following is true of $f$ ?

(A) $f$ has both a maximum and a minimum value.

(B) $f$ has a maximum value, but no minimum value.

(D) $f$ has neither a minimum value nor a maximum value.

▶️ Answer/Explanation

Detailed solution

The function $f(x) = \log_{3} x$ is strictly increasing over its entire domain.
At the right endpoint $x = 9$, the function reaches a maximum value of $f(9) = \log_{3} 9 = 2$.
As $x$ approaches the left boundary $0$ from the right, the function $f(x) \to -\infty$.
Because the interval is open at $x = 0$, the function decreases without bound.
Therefore, there is no minimum value because the function never reaches a lowest point.
The correct option is (B).

Question

The function $f$ is given by $f(x) = \ln x$. Which of the following describes input values for which the output values of $f$ are integers?

(A) Integer powers of $e$

(B) Integer powers of $10$

(D) Integers raised to the power $10$

▶️ Answer/Explanation

Detailed solution

The function is defined as $f(x) = \ln x$, where the base is $e$.
To find when the output is an integer, set $f(x) = n$, where $n$ is any integer.
This gives the equation $\ln x = n$.
By converting the logarithmic form to exponential form, we get $x = e^n$.
Therefore, the input values $x$ must be integer powers of $e$.
For example, if $x = e^2$, then $f(e^2) = \ln(e^2) = 2$, which is an integer.
This confirms that option (A) is the correct description.

Question

The function $f$ is logarithmic, and the points $(2, 1)$ and $(4, 2)$ are on the graph of $f$ in the $xy$-plane. Which of the following could define $f(x)$?

(A) $\log_{4} x$
(B) $2 \log_{2} x$
(C) $2 \log_{4} x$
(D) $\log_{4} (x + 2)$

▶️ Answer/Explanation

Detailed solution

To find the correct function, we test the given points $(2, 1)$ and $(4, 2)$ in each option.
For (A): $f(2) = \log_{4} 2 = 0.5$, which does not equal $1$.
For (B): $f(2) = 2 \log_{2} 2 = 2(1) = 2$, which does not equal $1$.
For (C): $f(2) = 2 \log_{4} 2 = 2(0.5) = 1$, which matches the first point.
Checking (C) with the second point: $f(4) = 2 \log_{4} 4 = 2(1) = 2$, which matches $(4, 2)$.
For (D): $f(2) = \log_{4} (2 + 2) = \log_{4} 4 = 1$, but $f(4) = \log_{4} 6 \neq 2$.
Therefore, the correct function is (C) $f(x) = 2 \log_{4} x$.

Question

The function $g$ is given by $g(x) = \log_{3} x$. What is the value of $g\left(\frac{1}{9}\right)$?

(A) $-2$

(B) $-\frac{1}{2}$

(D) $2$

▶️ Answer/Explanation

Detailed solution

To find the value of $g\left(\frac{1}{9}\right)$, substitute $x = \frac{1}{9}$ into the function $g(x) = \log_{3} x$.
This gives the expression $g\left(\frac{1}{9}\right) = \log_{3} \left(\frac{1}{9}\right)$.
Rewrite the fraction as a power of $3$ using the rule $\frac{1}{a^n} = a^{-n}$.
Since $9 = 3^2$, it follows that $\frac{1}{9} = 3^{-2}$.
Substitute this back to get $\log_{3} (3^{-2})$.
Using the property $\log_{b} (b^y) = y$, the expression simplifies to $-2$.
Therefore, the correct value is $-2$, which corresponds to option (A).

Question

Let $h$ be a function such that the output values of $h$ increase without bound as the input values increase without bound, and the output values of $h$ decrease without bound as the input values decrease arbitrarily close to $0$. Which of the following could be the graph of $h$?

(A)

(B)

(C)

(D)

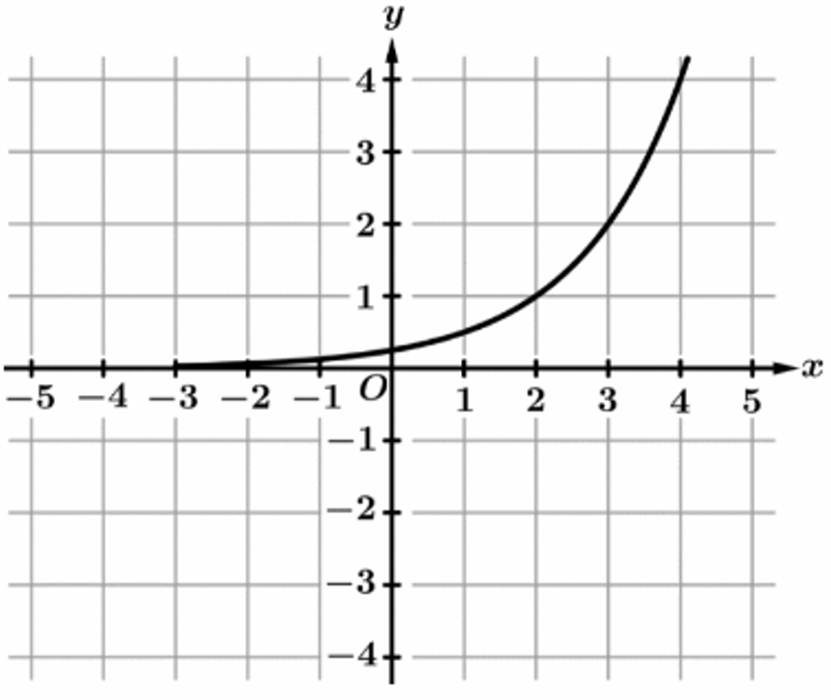
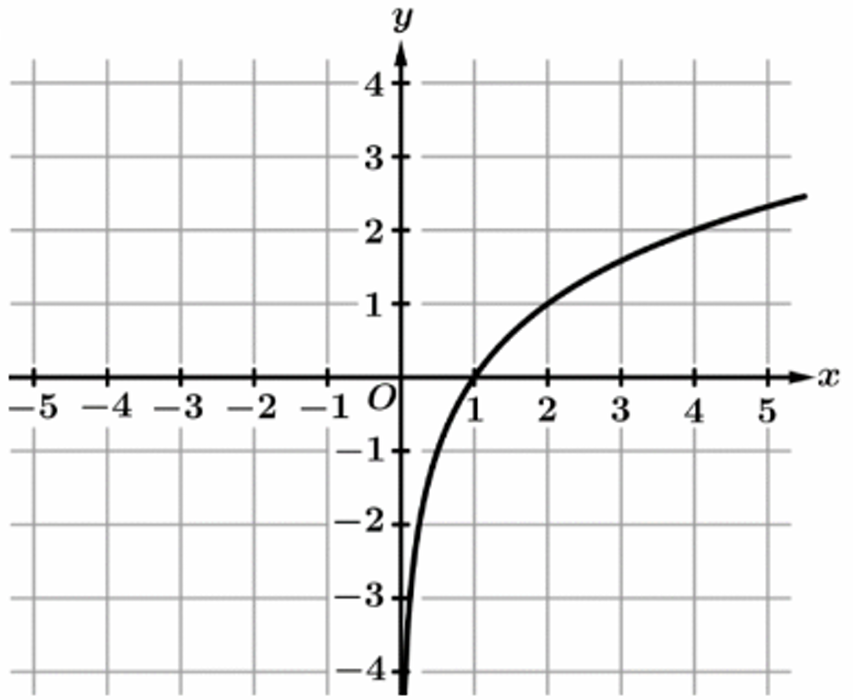
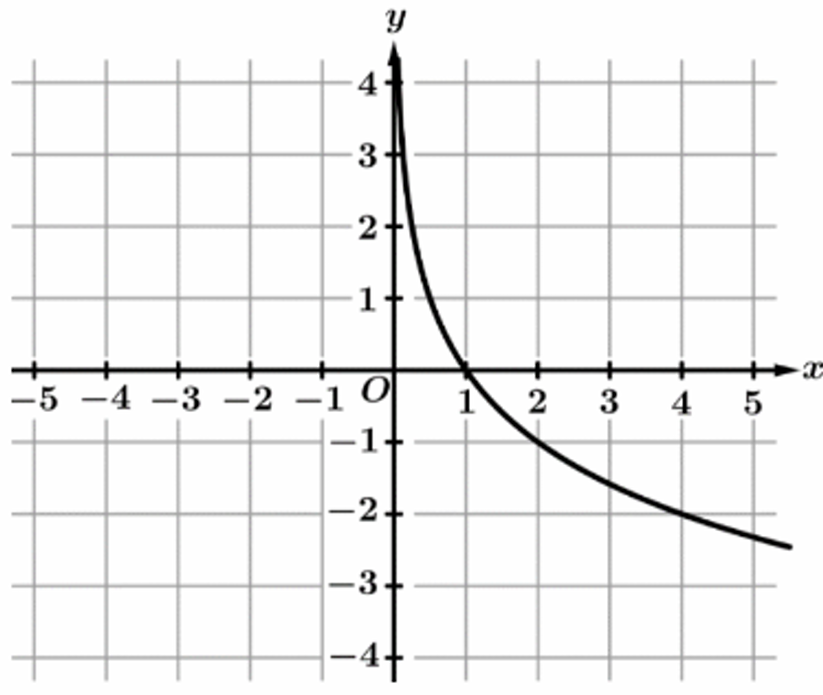
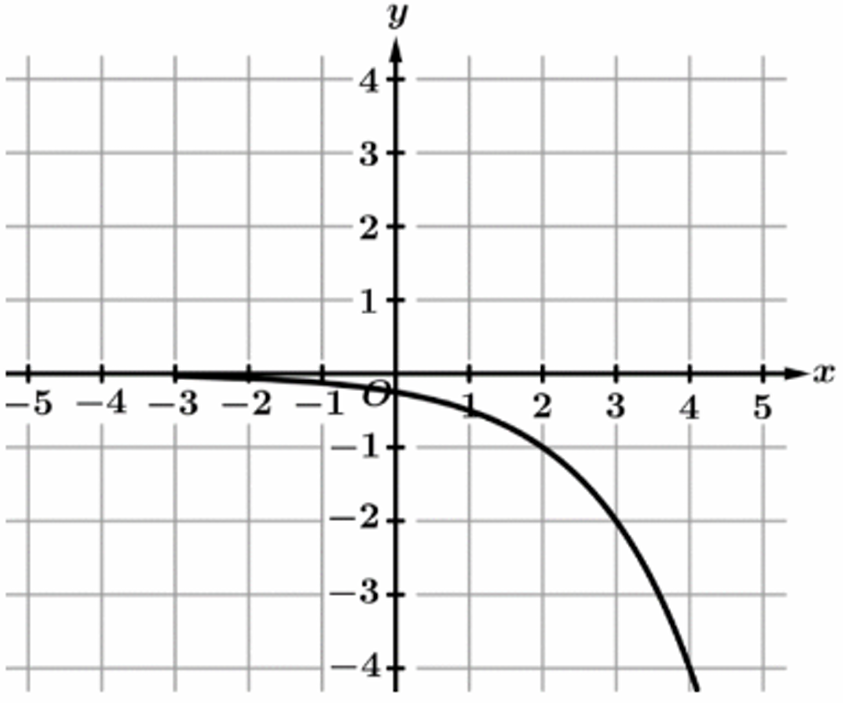
▶️ Answer/Explanation

Detailed solution

The correct graph is (B).
As $x \to \infty$, the output $h(x) \to \infty$, which is shown by the graph rising on the right.
As $x \to 0^+$, the output $h(x) \to -\infty$, indicating a vertical asymptote at $x = 0$.
Graph (A) represents an exponential growth function where $h(x) \to 0$ as $x \to -\infty$.
Graph (C) shows $h(x)$ decreasing as $x$ increases, contradicting the first condition.
Graph (D) shows $h(x) \to -\infty$ as $x \to \infty$, which also contradicts the prompt.
Only graph (B), typical of a logarithmic function $\log_b(x)$ where $b > 1$, fits both criteria.

Question

An increasing, continuous function $ g(x) $ has outputs of some values of $ x $ shown above. $ f(x) $ is a function shown to the right as the graph.

(A) i. Estimate the value of $ g(f^{-1}(1)) $ for all values if it is defined.

ii. If $ h(x) = \frac{g(x)}{f(x)} $, then define any discontinuities, their type, and their location when $ x > 0 $.

(B) Suppose $ j(x) = \frac{1}{4.99 – \ln(x)} \cdot e^{2 \sin (\sqrt{x})} $ could be used to model $ f(x) $.

i. Determine the end behavior of $ j $ when it increases without bound. Express your answer with the mathematical definition of a limit if it exists. If it does not exist, explain why.

ii. Determine the vertical asymptote of $ j $ when it approaches $ 0 $ from the right. Express your answer with the mathematical definition of a limit if it exists. If it does not, explain why.

(C) Determine if $ g(x) $, using the values in the table, can be best modeled with a linear, quadratic, exponential, or logarithmic function. Explain your answer based on the relationship between the change in the output values of $ g $ and the change in the input values of $ g $.

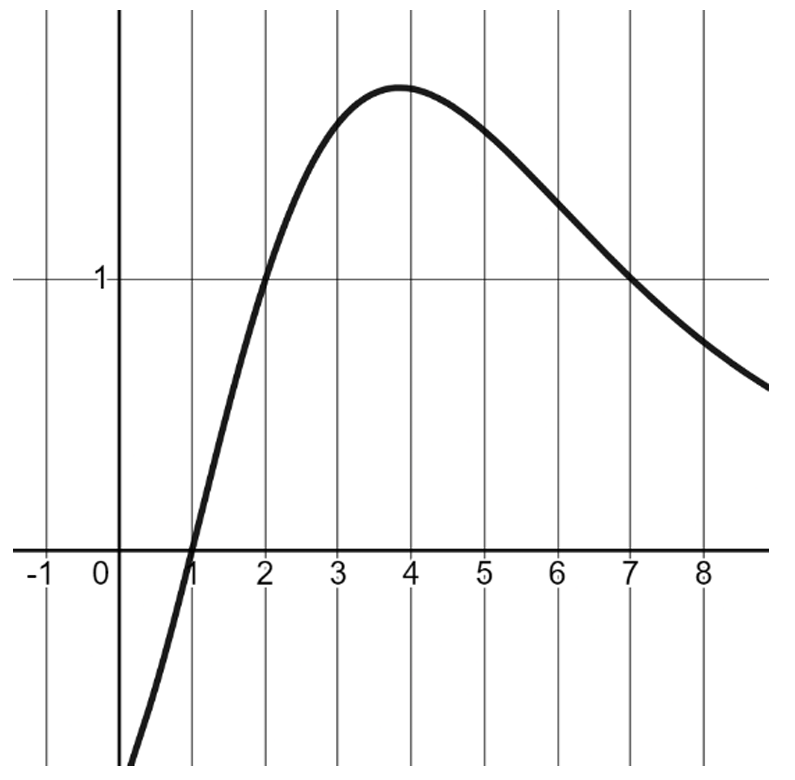
Most-appropriate topic codes (CED):

• TOPIC 2.8: Inverses of Exponential Functions — part (A)i
• TOPIC 1.10: Rational Functions and Holes — part (A)ii
• TOPIC 1.7: Rational Functions and End Behavior — part (B)i
• TOPIC 1.9: Rational Functions and Vertical Asymptotes — part (B)ii
• TOPIC 2.10: Logarithmic Function Context and Data Modeling — part (C)

▶️ Answer/Explanation

Detailed solution

(A)

i. The graph of $ f(x) $ shows that $ f(2) \approx 1 $, so $ f^{-1}(1) \approx 2 $. From the table, $ g(2) = 1 $. Thus, $ g(f^{-1}(1)) \approx 1 $.
Since $ f(x) $ is continuous and increasing, the inverse is defined for values in its range.
The estimate is a single value, $ 1 $, as the graph aligns precisely with the point. No other values exist due to the strictly increasing nature of $ f(x) $.

ii. The graph of $ f(x) $ crosses zero at $ x=1 $, so $ f(1)=0 $, and from the table, $ g(1)=0 $.
Thus, $ h(1) $ is undefined ($ 0/0 $ form).
The limit as $ x \to 1 $ of $ h(x) $ exists and equals $ 1 $, since both $ g(x) $ and $ f(x) $ resemble $ \log_2(x) $, making $ h(x)=1 $ elsewhere.
This indicates a removable discontinuity at $ x=1 $. No other discontinuities for $ x>0 $, as $ f(x) \neq 0 $ elsewhere in the domain.
The location is $ x=1 $, type: removable.

(B)

i. As $ x \to \infty $, $ \ln(x) \to \infty $, so $ 4.99 – \ln(x) \to -\infty $, and $ \frac{1}{4.99 – \ln(x)} \to 0^- $.
The term $ e^{2 \sin(\sqrt{x})} $ oscillates between $ e^{-2} $ and $ e^{2} $, remaining bounded.
By the squeeze theorem, since the amplitude approaches $ 0 $, $ \lim_{x \to \infty} j(x) = 0 $.
The end behavior is that $ j(x) $ approaches $ 0 $. The limit exists.

ii. As $ x \to 0^+ $, $ \ln(x) \to -\infty $, so $ 4.99 – \ln(x) \to +\infty $, and $ \frac{1}{4.99 – \ln(x)} \to 0^+ $.
Also, $ \sqrt{x} \to 0^+ $, $ \sin(\sqrt{x}) \to 0^+ $, so $ e^{2 \sin(\sqrt{x})} \to e^0 = 1 $.
Thus, $ j(x) \to 0 \cdot 1 = 0 $.
The limit is $ \lim_{x \to 0^+} j(x) = 0 $.
No vertical asymptote at $ x=0 $, as the function approaches a finite value, not $ \pm \infty $.

(C)

The table shows $ g(x) $ values: at $ x=0.5, 1, 2, 4, 7, 8 $, $ g(x)=-1, 0, 1, 2, 2.807, 3 $.
When $ x $ doubles ($ 0.5 $ to $ 1 $, $ 1 $ to $ 2 $, $ 2 $ to $ 4 $, $ 4 $ to $ 8 $), $ \Delta g = +1 $ consistently.
This pattern matches logarithmic functions, where outputs increase by a constant for multiplicative input changes.
Linear would require constant $ \Delta g $ for constant $ \Delta x $, but $ \Delta x $ varies while $ \Delta g =1 $ for doublings.
Quadratic would show constant second differences, but here first differences are not constant.
Exponential would show constant ratios in outputs for additive input changes, which does not fit.
Thus, best modeled by a logarithmic function like $ g(x) = \log_2(x) $.

Question

Directions:

Unless otherwise specified, the domain of a function $ f $ is assumed to be the set of all real numbers $ x $ for which $ f(x) $ is a real number. Angle measures for trigonometric functions are assumed to be in radians.
Solutions to equations must be real numbers. Determine the exact value of any expression that can be obtained without a calculator. For example, $ \log_2 8 $, $ \cos(\frac{\pi}{2}) $, and $ \sin^{-1}(1) $ can be evaluated without a calculator.
Unless otherwise specified, combine terms using algebraic methods and rules for exponents and logarithms, where applicable. For example, $ 2x + 3x $, $ 5^2 \cdot 5^3 $, $ \frac{x^5}{x^2} $, and $ \ln 3 + \ln 5 $ should be rewritten in equivalent forms.
For each part of the question, show the work that leads to your answers.

Part A
The functions $ g $ and $ h $ are given by

$ g(x) = \log_5(4x – 2) $
$ h(x) = \sin^{-1}(8x) $

(i) Solve $ g(x) = 3 $ for values of $ x $ in the domain of $ g $.

(ii) Solve $ h(x) = \frac{\pi}{4} $ for values of $ x $ in the domain of $ h $.

Part B
The functions $ j $ and $ k $ are given by

$ j(x) = (\sec x)(\cot x) $
$ k(x) = \frac{(16^{3x}) \cdot 4^x}{2} $

(i) Rewrite $ j(x) $ as an expression involving $ \sin x $ and no other trigonometric functions.

(ii) Rewrite $ k(x) $ as an expression of the form $ 4^{(ax+b)} $, where $ a $ and $ b $ are constants.

Part C
The function $ m $ is given by

$ m(x) = \sqrt{3}\tan(x + \frac{\pi}{2}) $.

Find all values in the domain of $ m $ that yield an output value of 1.

▶️ Answer/Explanation

Detailed solution

Part A
(i) Solve $ g(x) = 3 $
Start with the given equation:
$ \log_5(4x – 2) = 3 $
Convert the logarithmic equation to exponential form ($ y = \log_b x \iff x = b^y $):
$ 4x – 2 = 5^3 $
Evaluate the exponent:
$ 4x – 2 = 125 $
Add 2 to both sides:
$ 4x = 127 $
Divide by 4:
$ x = \frac{127}{4} $

(ii) Solve $ h(x) = \frac{\pi}{4} $
Start with the given equation:
$ \sin^{-1}(8x) = \frac{\pi}{4} $
Take the sine of both sides to isolate the argument:
$ 8x = \sin\left(\frac{\pi}{4}\right) $
Substitute the exact value of $ \sin\left(\frac{\pi}{4}\right) $:
$ 8x = \frac{\sqrt{2}}{2} $
Divide by 8:
$ x = \frac{\sqrt{2}}{16} $

Part B
(i) Rewrite $ j(x) $
Start with the function definition:
$ j(x) = (\sec x)(\cot x) $
Substitute the reciprocal and quotient identities ($ \sec x = \frac{1}{\cos x} $ and $ \cot x = \frac{\cos x}{\sin x} $):
$ j(x) = \left(\frac{1}{\cos x}\right) \left(\frac{\cos x}{\sin x}\right) $
Cancel the $ \cos x $ terms:
$ j(x) = \frac{1}{\sin x} $

(ii) Rewrite $ k(x) $
Start with the function definition:
$ k(x) = \frac{(16^{3x}) \cdot 4^x}{2} $
To write in the form $ 4^{(ax+b)} $, convert bases 16 and 2 to base 4.
Since $ 16 = 4^2 $ and $ 2 = \sqrt{4} = 4^{1/2} = 4^{0.5} $:
$ k(x) = \frac{(4^2)^{3x} \cdot 4^x}{4^{0.5}} $
Apply the power of a power rule ($ (a^m)^n = a^{mn} $):
$ k(x) = \frac{4^{6x} \cdot 4^x}{4^{0.5}} $
Apply the product rule for exponents ($ a^m \cdot a^n = a^{m+n} $) in the numerator:
$ k(x) = \frac{4^{6x + x}}{4^{0.5}} = \frac{4^{7x}}{4^{0.5}} $
Apply the quotient rule for exponents ($ \frac{a^m}{a^n} = a^{m-n} $):
$ k(x) = 4^{7x – 0.5} $ (or $ 4^{7x – \frac{1}{2}} $)
Thus, $ a = 7 $ and $ b = -0.5 $.

Part C
Find values where $ m(x) = 1 $
Set the function equal to 1:
$ \sqrt{3}\tan\left(x + \frac{\pi}{2}\right) = 1 $
Isolate the tangent function by dividing by $ \sqrt{3} $:
$ \tan\left(x + \frac{\pi}{2}\right) = \frac{1}{\sqrt{3}} $
Determine the reference angle. We know that $ \tan\left(\frac{\pi}{6}\right) = \frac{1}{\sqrt{3}} $.
Set up the general solution for tangent ($ \theta = \text{ref} + n\pi $):
$ x + \frac{\pi}{2} = \frac{\pi}{6} + n\pi $, where $ n $ is any integer.
Solve for $ x $ by subtracting $ \frac{\pi}{2} $ from both sides:
$ x = \frac{\pi}{6} – \frac{\pi}{2} + n\pi $
Find a common denominator (6) to combine fractions:
$ x = \frac{\pi}{6} – \frac{3\pi}{6} + n\pi $
$ x = -\frac{2\pi}{6} + n\pi $
Simplify the fraction:
$ x = -\frac{\pi}{3} + n\pi $

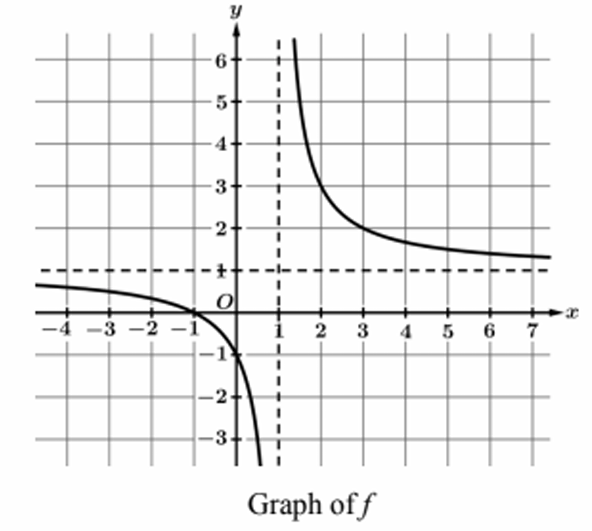
Question

The figure shows the graph of the decreasing function $ f $ on its domain of all real numbers where $ x \neq 1 $. The points $ (-1, 0) $ and $ (3, 2) $ are on the graph of $ f $. The function $ g $ is given by $ g(x) = 2 + 3\ln x $.

(A) (i) The function $ h $ is defined by $ h(x) = (g \circ f)(x) = g(f(x)) $. Find the value of $ h(3) $ as a decimal approximation, or indicate that it is not defined.

(ii) Find all real zeros of $ f $, or indicate there are no real zeros.

(B) (i) Find all values of $ x $, as decimal approximations, for which $ g(x) = e $, or indicate there are no such values.

(ii) Determine the end behavior of $ g $ as $ x $ increases without bound. Express your answer using the mathematical notation of a limit.

(ii) Give a reason for your answer based on the definition of a function and the graph of $ y = f(x) $.

▶️ Answer/Explanation

Detailed solution

(A)(i) Find $ h(3) $
The function is defined as $ h(x) = g(f(x)) $.
First, we find the value of the inner function, $ f(3) $.
According to the problem text and graph, the point $ (3, 2) $ lies on the graph of $ f $. Therefore, $ f(3) = 2 $.
Now, substitute this value into the outer function $ g(x) $:
$ h(3) = g(2) $
Using the definition $ g(x) = 2 + 3\ln x $:
$ g(2) = 2 + 3\ln(2) $
Using a calculator to approximate $ \ln(2) \approx 0.693 $:
$ g(2) = 2 + 3(0.6931…) \approx 2 + 2.079 = 4.079 $
Answer: $ h(3) \approx 4.079 $

(A)(ii) Find real zeros of $ f $
A real zero of a function occurs where the graph intersects the x-axis (where $ f(x) = 0 $).
Looking at the provided graph, the curve intersects the x-axis at $ x = -1 $.
The problem text confirms the point $ (-1, 0) $ is on the graph.
There are no other intersections with the x-axis shown.
Answer: $ x = -1 $

(B)(i) Find $ x $ for $ g(x) = e $
Set up the equation:
$ 2 + 3\ln x = e $
Subtract 2 from both sides:
$ 3\ln x = e – 2 $
Divide by 3:
$ \ln x = \frac{e – 2}{3} $
Convert from logarithmic to exponential form to solve for $ x $:
$ x = e^{\left(\frac{e – 2}{3}\right)} $
Approximating the value (using $ e \approx 2.718 $):
$ x \approx e^{0.2394} $
Answer: $ x \approx 1.271 $

(B)(ii) End behavior of $ g $
We need to evaluate the limit as $ x \to \infty $ for $ g(x) = 2 + 3\ln x $.
As $ x $ increases without bound ($ x \to \infty $), the natural logarithm function $ \ln x $ also increases without bound ($ \ln x \to \infty $).
Multiplying by 3 and adding 2 does not change the unbounded nature.
Answer: $ \lim_{x \to \infty} g(x) = \infty $

(C)(i) Is $ f $ invertible?
Answer: Yes, $ f $ is invertible.

(C)(ii) Reason
A function is invertible if and only if it is one-to-one. This can be verified visually using the Horizontal Line Test.
Looking at the graph of $ f(x) $:
1. The function is strictly decreasing on both branches of its domain ($ x < 1 $ and $ x > 1 $).
2. The range of the left branch appears to be $ (-\infty, 1) $ and the range of the right branch appears to be $ (1, \infty) $.
Because the y-values do not repeat (no horizontal line intersects the graph more than once), the function is one-to-one.
Therefore, $ f $ has an inverse.

AP Precalculus -2.11 Logarithmic Functions- MCQ Exam Style Questions - Effective Fall 2023