AP Precalculus -2.12 Logarithmic Function Manipulation- Study Notes - Effective Fall 2023
AP Precalculus -2.12 Logarithmic Function Manipulation- Study Notes – Effective Fall 2023
AP Precalculus -2.12 Logarithmic Function Manipulation- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Rewrite logarithmic expressions in equivalent forms.
Key Concepts:
Product Property for Logarithms and Transformations
Power Property for Logarithms and Vertical Dilations
Change of Base Property for Logarithms
The Natural Logarithmic Function
Product Property for Logarithms and Transformations
The product property for logarithms states that the logarithm of a product can be written as the sum of two logarithms.
\( \mathrm{ \displaystyle \log_b(xy)=\log_b x+\log_b y } \)
This property is valid when \( \mathrm{x>0} \), \( \mathrm{y>0} \), \( \mathrm{b>0} \), and \( \mathrm{b\ne1} \).
Using this property, a logarithmic function with a multiplicative factor inside the argument can be rewritten in an equivalent form.
For example:
\( \mathrm{ \displaystyle f(x)=\log_b(kx) } \)
can be rewritten using the product property as
\( \mathrm{ \displaystyle f(x)=\log_b k+\log_b x } \)
Let
\( \mathrm{ \displaystyle a=\log_b k } \)
Then the function becomes
\( \mathrm{ \displaystyle f(x)=a+\log_b x } \)
Graphical Interpretation
This shows that a horizontal dilation of a logarithmic function is equivalent to a vertical translation.
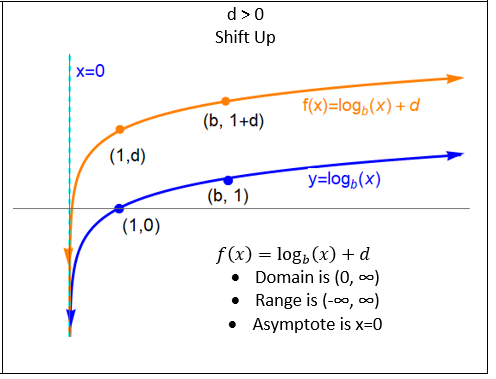
• Multiplying the input by \( \mathrm{k} \) shifts the graph vertically
• The vertical shift amount is \( \mathrm{\log_b k} \)
Example
Rewrite the function in the form \( \mathrm{a+\log_b x} \):
\( \mathrm{ \displaystyle f(x)=\log_2(4x) } \)
▶️ Answer/Explanation
Apply the product property:
\( \mathrm{ \displaystyle \log_2(4x)=\log_2 4+\log_2 x } \)
Since \( \mathrm{\log_2 4=2} \), the function becomes
\( \mathrm{ \displaystyle f(x)=2+\log_2 x } \)
Conclusion
The graph of \( \mathrm{\log_2(4x)} \) is the graph of \( \mathrm{\log_2 x} \) shifted upward by 2 units.
Example
Describe the transformation of the graph:
\( \mathrm{ \displaystyle f(x)=\log_{10}(0.1x) } \)
▶️ Answer/Explanation
Rewrite using the product property:
\( \mathrm{ \displaystyle \log_{10}(0.1x)=\log_{10}0.1+\log_{10}x } \)
Since \( \mathrm{\log_{10}0.1=-1} \),
\( \mathrm{ \displaystyle f(x)=\log_{10}x-1 } \)
Conclusion
The graph is shifted downward by 1 unit compared to \( \mathrm{y=\log_{10}x} \).
Power Property for Logarithms and Vertical Dilations
The power property for logarithms states that a logarithm of a power can be rewritten by moving the exponent outside as a multiplier.
\( \mathrm{ \displaystyle \log_b(x^n)=n\log_b x } \)
This property is valid for \( \mathrm{x>0} \), \( \mathrm{b>0} \), and \( \mathrm{b\ne1} \).
Using this property, a logarithmic function with a power applied to the input can be rewritten in an equivalent form.
If
\( \mathrm{ \displaystyle f(x)=\log_b(x^k) } \)
then
\( \mathrm{ \displaystyle f(x)=k\log_b x } \)
Graphical Interpretation
This shows that raising the input of a logarithmic function to a power results in a vertical dilation of the graph.
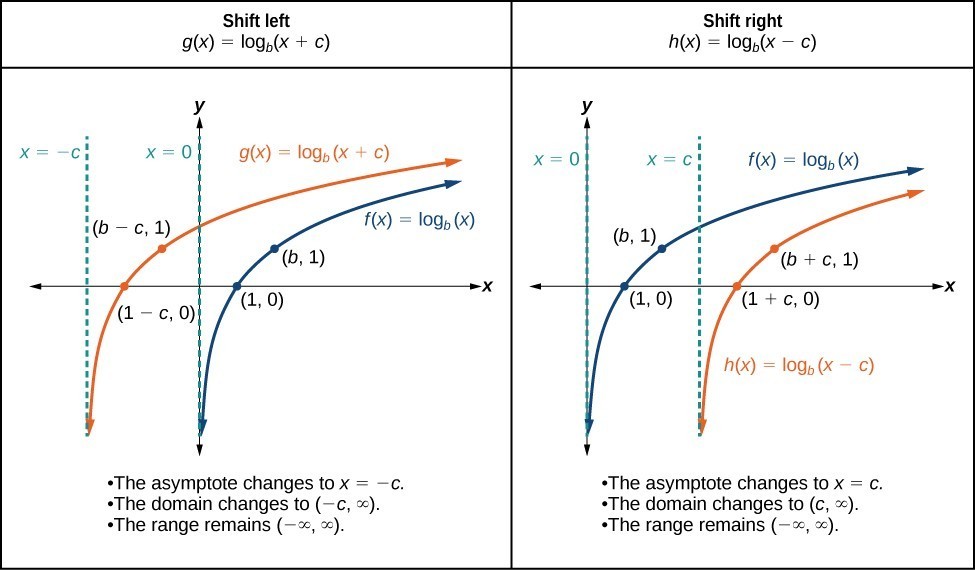
• If \( \mathrm{k>1} \), the graph is vertically stretched
• If \( \mathrm{0<k<1} \), the graph is vertically compressed
• If \( \mathrm{k<0} \), the graph is reflected across the x-axis
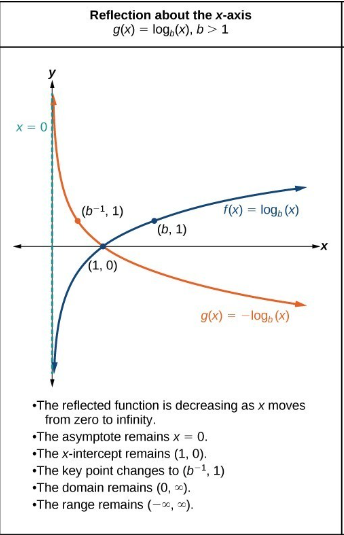
Example
Rewrite the function in equivalent form and describe the transformation:
\( \mathrm{ \displaystyle f(x)=\log_3(x^4) } \)
▶️ Answer/Explanation
Apply the power property:
\( \mathrm{ \displaystyle \log_3(x^4)=4\log_3 x } \)
Conclusion
The graph is a vertical stretch of \( \mathrm{y=\log_3 x} \) by a factor of 4.
Example
Describe the effect of the exponent in the function
\( \mathrm{ \displaystyle f(x)=\log_{10}(x^{1/2}) } \)
▶️ Answer/Explanation
Rewrite using the power property:
\( \mathrm{ \displaystyle \log_{10}(x^{1/2})=\dfrac12\log_{10}x } \)
Conclusion
The graph is vertically compressed by a factor of \( \mathrm{\dfrac12} \) compared to \( \mathrm{y=\log_{10}x} \).
Change of Base Property for Logarithms
The change of base property for logarithms allows a logarithm with any base to be rewritten using a different base.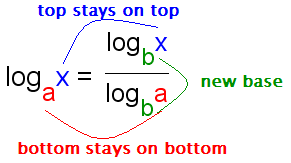
\( \mathrm{ \displaystyle \log_b x=\dfrac{\log_a x}{\log_a b} } \)
where \( \mathrm{a>0} \) and \( \mathrm{a\ne1} \).
A common choice is \( \mathrm{a=10} \) or \( \mathrm{a=e} \), which allows logarithmic values to be computed using calculators or technology.
Graphical Interpretation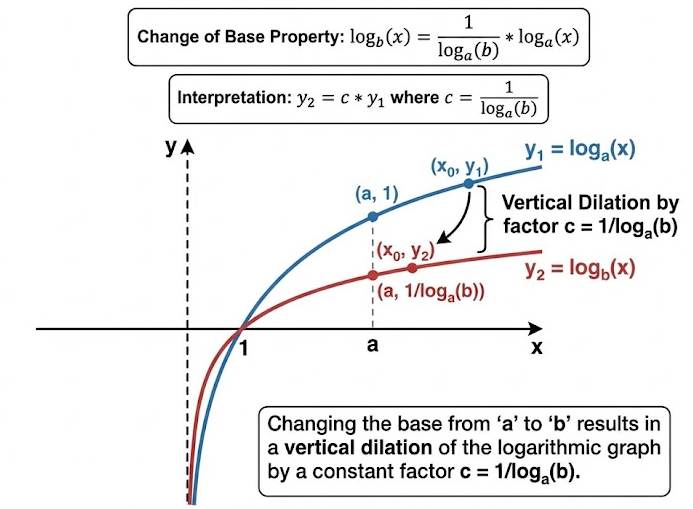
Using the change of base property,
\( \mathrm{ \displaystyle \log_b x=\dfrac{1}{\log_a b}\log_a x } \)
This shows that changing the base of a logarithm results in a vertical dilation of the logarithmic graph.
• The factor \( \mathrm{\dfrac{1}{\log_a b}} \) controls the vertical stretch or compression
• The domain \( \mathrm{x>0} \) and vertical asymptote \( \mathrm{x=0} \) remain unchanged
Therefore, all logarithmic functions are vertical dilations of one another.
Example
Rewrite the logarithm using base 10:
\( \mathrm{ \displaystyle \log_3 x } \)
▶️ Answer/Explanation
Apply the change of base formula:
\( \mathrm{ \displaystyle \log_3 x=\dfrac{\log x}{\log 3} } \)
Conclusion
The graph of \( \mathrm{y=\log_3 x} \) is a vertical stretch of \( \mathrm{y=\log x} \) by a factor of \( \mathrm{\dfrac{1}{\log 3}} \).
Example
Explain how the graphs of \( \mathrm{y=\log_2 x} \) and \( \mathrm{y=\log_{10} x} \) are related.
▶️ Answer/Explanation
Using change of base,
\( \mathrm{ \displaystyle \log_2 x=\dfrac{\log x}{\log 2} } \)
This shows that \( \mathrm{y=\log_2 x} \) is a vertical stretch of \( \mathrm{y=\log x} \) by a factor of \( \mathrm{\dfrac{1}{\log 2}} \).
Conclusion
Changing the base changes only the vertical scale of the graph, not its overall shape or domain.
The Natural Logarithmic Function
The natural logarithmic function is a logarithmic function whose base is the number \( \mathrm{e} \).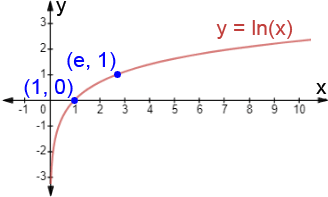
It is written as
\( \mathrm{ \displaystyle f(x)=\ln x } \)
and is defined by the equivalence
\( \mathrm{ \displaystyle \ln x=\log_e x } \)
The number \( \mathrm{e} \) is an irrational constant approximately equal to \( \mathrm{2.718} \) and arises naturally in many growth and decay processes.
Key Properties of \( \mathrm{\ln x} \)
• Domain: \( \mathrm{x>0} \)
• Range: all real numbers
• Vertical asymptote: \( \mathrm{x=0} \)
• Inverse of the exponential function \( \mathrm{y=e^x} \)
Like all logarithmic functions with base greater than 1, \( \mathrm{\ln x} \) is always increasing and concave down.
Example
Evaluate the natural logarithm
\( \mathrm{ \displaystyle \ln e^4 } \)
▶️ Answer/Explanation
Since logarithms and exponentials with the same base are inverses:
\( \mathrm{ \displaystyle \ln(e^4)=4 } \)
Example
Rewrite the logarithm using natural logarithms:
\( \mathrm{ \displaystyle \log_5 x } \)
▶️ Answer/Explanation
Apply the change of base formula with base \( \mathrm{e} \):
\( \mathrm{ \displaystyle \log_5 x=\dfrac{\ln x}{\ln 5} } \)
Conclusion
Natural logarithms allow logarithms with any base to be expressed in terms of \( \mathrm{e} \).
