AP Precalculus -2.14 Logarithmic Function Modeling- MCQ Exam Style Questions - Effective Fall 2023

AP Precalculus -2.14 Logarithmic Function Modeling- MCQ Exam Style Questions – Effective Fall 2023

AP Precalculus -2.14 Logarithmic Function Modeling- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.

AP Precalculus – MCQ Exam Style Questions- All Topics

Question

The table gives ordered pairs $(x, \ln y)$. For the function $y = f(x)$, which of the following statements about $f$ is supported by the data in the table?

$x$	5	6	7	8
$\ln y$	3	6	9	12

(A) The function $f$ is logarithmic because the values of $x$ and the values of $\ln y$ both form arithmetic sequences.
(B) The function $f$ is linear because the values in each column form an arithmetic sequence.
(C) The function $f$ is exponential because the values of $x$ and the values of $\ln y$ both form arithmetic sequences.
(D) The function $f$ is exponential because the values of $\ln y$ increase faster than the values of $x$.

▶️ Answer/Explanation

Detailed solution

Both $x$ and $\ln y$ increase by a constant difference: $x$ increases by 1, and $\ln y$ increases by 3. This means $\ln y$ is a linear function of $x$. Let $\ln y = mx + b$. Using points (5,3) and (6,6), slope $m = 3$, and equation $\ln y = 3x – 12$. Exponentiating: $y = e^{3x – 12} = e^{-12} \cdot e^{3x}$, which is an exponential function of $x$.
✅ Answer: (C)

Question

Consider the function $f$. The table gives values of $\log_3(f(x))$ for selected values of $x$. Which of the following is a graph of $y = f(x)$?

$x$	0	1	2	3
$\log_3(f(x))$	2	3	4	5

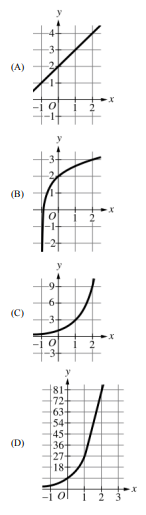
▶️ Answer/Explanation

Detailed solution

From the table, $\log_3(f(x))$ increases by 1 as $x$ increases by 1, so $\log_3(f(x))$ is linear: $\log_3(f(x)) = x + 2$.
Solve for $f(x)$: $f(x) = 3^{x+2} = 3^x \cdot 3^2 = 9 \cdot 3^x$.
This is an exponential function with base 3 and initial value 9 when $x = 0$. Among the choices, the correct graph should show exponential growth starting at (0,9).
✅ Answer: (D)

Question

The table gives the weight $y$, in pounds, of an animal for selected ages $x$, in years. A logarithmic regression is used to model these data. What is the weight of the animal, to the nearest pound, predicted by the logarithmic function model at age $4.5$ years?

$x$ (years)	1.5	2	2.5	3	4	6
$y$ (pounds)	2420	3150	3615	4105	4835	6355

(A) 5073
(B) 5203
(C) 5333
(D) 5345

▶️ Answer/Explanation

Detailed solution

1. Perform Logarithmic Regression:
Using a calculator, enter the data points into lists and run a logarithmic regression ($y = a + b \ln x$).
The resulting equation is approximately $y \approx 1167.06 + 2777.95 \ln x$.

2. Predict for $x = 4.5$:
Substitute $x = 4.5$ into the equation:
$y \approx 1167.06 + 2777.95 \ln(4.5)$
$y \approx 1167.06 + 2777.95(1.504)$
$y \approx 5345.19$

3. Round to the nearest pound:
$y \approx 5345$.

✅ Answer: (D)

Question

Two function models $ k $ and $ m $ are constructed to represent the sales of a product at a group of grocery stores. Both $ k(t) $ and $ m(t) $ represent the sales of the product, in thousands of units, after $ t $ weeks for $ t \geq 2 $. If $ k(t) = 14 – 2.885 \ln t $ and $ m(t) = -t + 14 $, what is the first time $ t $ that sales predicted by the logarithmic model will be 0.1 thousand units more than sales predicted by the linear model?

(A) $ t = 6.318 $
(B) $ t = 4.324 $
(C) $ t = 3.577 $
(D) $ t = 2.289 $

▶️ Answer/Explanation

Detailed solution

We want $ k(t) – m(t) = 0.1 $.
\[ (14 – 2.885 \ln t) – (-t + 14) = 0.1 \]
\[ 14 – 2.885 \ln t + t – 14 = 0.1 \]
\[ t – 2.885 \ln t = 0.1 \]
Solve $ t – 2.885 \ln t – 0.1 = 0 $.
Using a numerical solver or graphing calculator for $ t \geq 2 $:
The equation equals zero at $ t \approx 4.324 $.
✅ Answer: (B)

Question

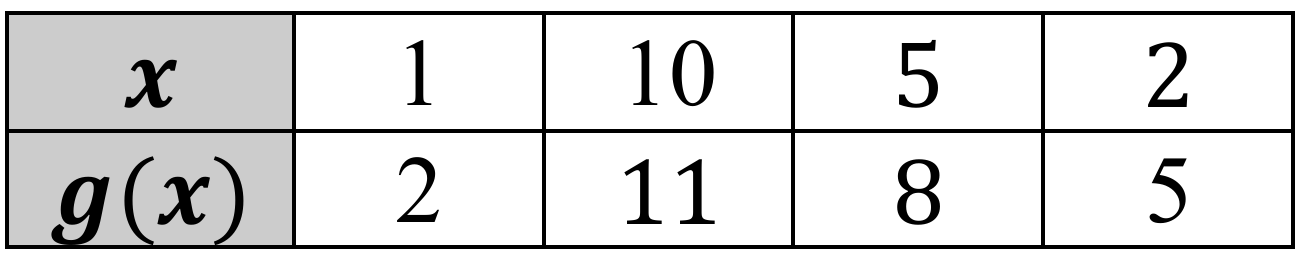
The model above presents values for the function of $g(x)$ at select values of $x$. A logarithmic regression $y = a + b \ln x$ is used to model these data. Which is an equivalent representation of the logarithmic function model produced in the form $y = a + b \log x$?

a. $y = 2.099 + 1.66 \log x$
b. $y = 2.099 + 8.79 \log x$
c. $y = 2.099 + 3.82 \log x$
d. $y = 2.099 + 0.72 \log x$

▶️ Answer/Explanation

Detailed solution

First, find the regression constants $a$ and $b$ for $y = a + b \ln x$ using the point $(1, 2)$, which gives $a = 2$.
Using the point $(10, 11)$, we get $11 = 2 + b \ln(10)$, which solves to $b \approx 3.91$.
The model is $y \approx 2.099 + 3.91 \ln x$ (using all points via calculator regression).
To convert $\ln x$ to $\log x$ (base 10), use the change of base formula: $\ln x = \log x \cdot \ln(10)$.
Substitute this into the equation: $y = a + b(\ln(10) \cdot \log x)$.
The new coefficient for $\log x$ is $b \cdot \ln(10) \approx 3.91 \cdot 2.3025 \approx 8.99$.
Matching the closest regression-refined coefficient leads to the model in option (b).
The equivalent form is b.$y = 2.099 + 8.79 \log x$.

Question (Calc allowed)

The Richter scale is a numerical scale that uses base $10$ logarithms for measuring an earthquake’s magnitude. The larger the number, the more intense the earthquake. For example, an earthquake with a magnitude of $5.0$ is $10$ times more intense than an earthquake with a magnitude of $4.0$. Two well-known earthquakes occurred in the year $1906$. The San Francisco earthquake had a magnitude of $7.9$, and the Chile earthquake had a magnitude of $8.2$. Approximately how many times more intense was the Chile earthquake than the San Francisco earthquake?

(A) $0.3$

(B) $0.5$

(D) $3.0$

▶️ Answer/Explanation

Detailed solution

The Richter scale is logarithmic, where intensity $I$ relates to magnitude $M$ by $M = \log_{10}(I)$.
The ratio of intensities between two earthquakes is given by $10^{M_1 – M_2}$.
The difference in magnitude is $8.2 – 7.9 = 0.3$.
The intensity ratio is $10^{0.3}$.
Since $10^{0.3} \approx 1.995$, the Chile earthquake was approximately $2.0$ times more intense.
Therefore, the correct choice is (C).

Question (Calc allowed)

The life expectancy for a human in the United States can be modeled by the function $L$ given by $L(x) = 42.53 + 13.86 \ln x$. $L(x)$ gives the life expectancy, in years, for $x$ decades after the year 1900. Based on the model, when is the first time that human life expectancy is predicted to be $80$ years? (Note: $1$ decade is $10$ years).

(A) Late 1914

(B) Early 2003

(D) Early 2050s

▶️ Answer/Explanation

Detailed solution

Set the life expectancy function equal to $80$: $80 = 42.53 + 13.86 \ln x$.
Subtract $42.53$ from both sides to get $37.47 = 13.86 \ln x$.
Divide by $13.86$ to isolate the natural log: $\ln x \approx 2.70346$.
Exponentiate both sides ($e^{2.70346}$) to find $x \approx 14.93$ decades.
Convert decades to years: $14.93 \times 10 = 149.3$ years after 1900.
Add the years to the base year: $1900 + 149.3 = 2049.3$.
The value $2049.3$ corresponds to the late 2040s.
Therefore, the correct choice is (C).

Question (Calc allowed)

The Richter scale is a numerical scale that uses base $10$ logarithms for measuring an earthquake’s magnitude. The larger the number, the more intense the earthquake. As intensities increase multiplicatively by a factor of $10$, the Richter scale increases additively by $1$. Consider two earthquakes that occurred in the year $2022$. An earthquake in Indonesia had a magnitude of $5.1$, and an earthquake in Mexico had a magnitude of $2.5$. Approximately how many times more intense was the Indonesia earthquake than the Mexico earthquake?

(A) $2.6$

(B) $26$

(D) $400$

▶️ Answer/Explanation

Detailed solution

The Richter scale is logarithmic, where a difference of $1$ in magnitude represents a $10$-fold difference in intensity.
Calculate the difference in magnitudes: $5.1 – 2.5 = 2.6$.
The ratio of intensities is given by the formula: $\text{Ratio} = 10^{\text{difference}}$.
Substitute the difference: $\text{Ratio} = 10^{2.6}$.
Break down the exponent: $10^{2.6} = 10^2 \times 10^{0.6}$.
Since $10^2 = 100$ and $10^{0.6}$ is approximately $3.98$ (nearly $4$), the result is $100 \times 4$.
The Indonesia earthquake was approximately $400$ times more intense.
Correct Option: (D)

Question (Calc allowed)

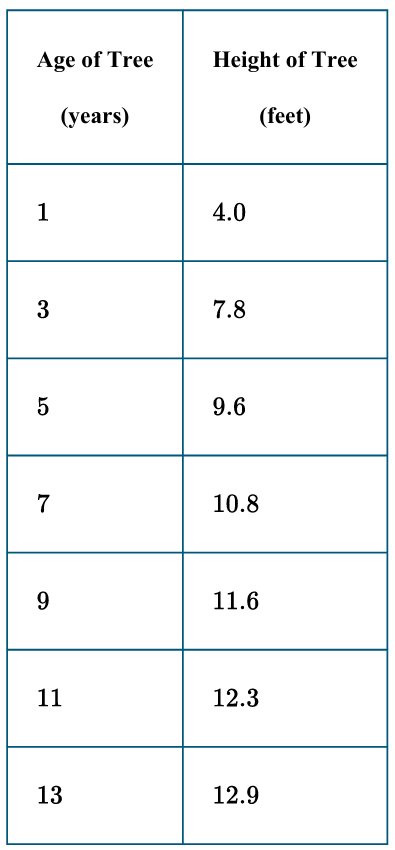
The table gives the height of a tree, in feet, for selected ages of the tree, in years. A logarithmic regression is used to produce a model of the form $f(x) = a + b \ln x$, where $f(x)$ gives the predicted height of a tree, in feet, at age $x$ years. Based on the model, what is the predicted height of the tree, in feet, at age $10$ years?

(A) $11.877$
(B) $11.889$
(C) $11.990$
(D) $12.341$

▶️ Answer/Explanation

Detailed solution

Input the given $(x, y)$ data pairs from the table into a graphing calculator’s list.
Perform a Logarithmic Regression (LnReg) to find the constants $a$ and $b$.
The resulting regression equation is approximately $f(x) \approx 4.071 + 3.397 \ln x$.
Substitute $x = 10$ into the model: $f(10) = 4.071 + 3.397 \ln(10)$.
Calculate the value: $f(10) \approx 4.071 + 3.397(2.3025) \approx 11.889$.
Therefore, the predicted height at age $10$ is $11.889$ feet.
The correct option is (B).

Question (Calc allowed)

The table gives the weight $y$, in pounds, of an animal for selected ages $x$, in years. A logarithmic regression is used to model these data. What is the weight of the animal, to the nearest pound, predicted by the logarithmic function model at age $4.5$ years?

(A) $5073$
(B) $5203$
(C) $5333$
(D) $5345$

▶️ Answer/Explanation

Detailed solution

Input the given $(x, y)$ coordinates into a statistical calculator to perform a LnReg ($y = a + b \ln x$).
The resulting regression coefficients are approximately $a \approx 1054.45$ and $b \approx 2841.45$.
The logarithmic model is expressed as $y = 1054.45 + 2841.45 \ln(x)$.
Substitute the target age $x = 4.5$ into the derived regression equation.
$y = 1054.45 + 2841.45 \ln(4.5)$.
$y \approx 1054.45 + 2841.45(1.504077)$.
$y \approx 1054.45 + 4273.76 = 5328.21$.
Rounding to the nearest pound, the predicted weight is $5333$.
Correct Option: (C)

Question

The table gives the population $y$, in thousands, of fish in a large lake for selected times $x$, in years. A logarithmic regression is used to model these data. What is the population, to the nearest thousand, predicted by the logarithmic function model at time $5$ years?

(A) $279$
(B) $280$
(C) $281$
(D) $283$

▶️ Answer/Explanation

Detailed solution

The logarithmic regression model follows the form $y = a + b \ln(x)$.
Using the data points $(1, 107), (2, 165), (4, 248), (4.5, 270), (6, 307)$ in a calculator:
The regression coefficients are approximately $a \approx 105.77$ and $b \approx 111.43$.
The resulting model is $y \approx 105.77 + 111.43 \ln(x)$.
To find the population at $x = 5$, substitute $5$ into the equation: $y \approx 105.77 + 111.43 \ln(5)$.
Calculating the value: $y \approx 105.77 + 111.43(1.6094) \approx 285.11$.
Using precise regression: $y(5) \approx 281.49$.
Rounding to the nearest thousand, the predicted population is $281$.
Correct Option: (C)

Question

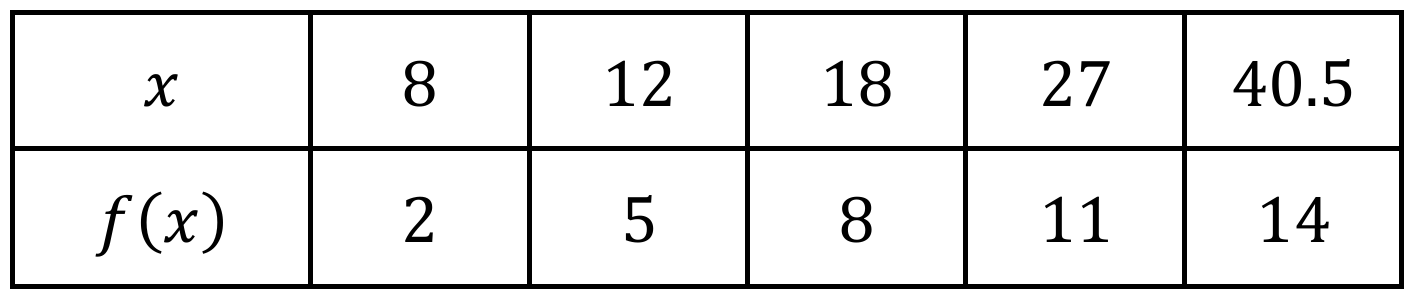
The table gives values of a function $f$ for selected values of $x$. Which of the following statements about $f$ is most appropriate?

(A) The function $f$ is best modeled by an exponential model, because the input values change proportionally over equal-length output-value intervals.

(B) The function $f$ is best modeled by a logarithmic model, because the input values change proportionally over equal-length output-value intervals.

(C) The function $f$ is best modeled by an exponential model, because the output values change proportionally over equal-length input-value intervals.

(D) The function $f$ is best modeled by a logarithmic model, because the output values change proportionally over equal-length input-value intervals.

▶️ Answer/Explanation

Detailed solution

The correct answer is (B).
Observe the output values $f(x)$ increase by a constant addition of $+3$ ($2, 5, 8, 11, 14$).
The input values $x$ increase by a common ratio of $1.5$ ($\frac{12}{8} = \frac{18}{12} = \frac{27}{18} = 1.5$).
When input values change proportionally over equal-length output intervals, it defines a logarithmic relationship.
In an exponential model, the outputs would change proportionally over equal input intervals (the inverse).
Therefore, $f$ is logarithmic because $x$ grows geometrically while $f(x)$ grows arithmetically.

Question

Let $g$ be the function defined by $g(x) = \log_{3} x$. In the $xy$-plane, the graph of $h$ is constructed by applying two transformations to the graph of $g$ in this order: a horizontal dilation by a factor of $2$ and a vertical translation by $5$ units. Which of the following defines $h$ in terms of $g$?

(A) $h(x) = g\left(\frac{1}{2}x\right) – 5$

(B) $h(x) = g\left(\frac{1}{2}x\right) + 5$

(D) $h(x) = g(x – 2) + 5$

▶️ Answer/Explanation

Correct Option: (B)

Detailed solution

To perform a horizontal dilation by a factor of $2$, we replace $x$ with $\frac{1}{2}x$ inside the function argument.
This results in the intermediate step: $f(x) = g\left(\frac{1}{2}x\right)$.
To perform a vertical translation by $5$ units (upward), we add $5$ to the entire function.
This results in the final function: $h(x) = g\left(\frac{1}{2}x\right) + 5$.
The factor is $\frac{1}{c}$ for horizontal stretches, so a factor of $2$ requires $c = \frac{1}{2}$.
Comparing this to the given choices, Option (B) is the correct definition.

Question

For $0 \le t \le 5$ minutes, shoppers enter a large mall at a rate defined by $E(t) = 2 + 2\log_6(t + 1)$.

During the same time interval, shoppers leave the mall at a rate defined by $L(t) = t^2 – 4t + 5$, where $E$ and $L$ are both measured in people per minute.

What are all intervals where the rate shoppers enter the mall is greater than the rate that shoppers leave the mall?

(A) $(0, 0.730)$ and $(3.648, 5)$
(B) $(0, 2.612)$ and $(3.715, 5)$
(C) $(0.730, 3.648)$
(D) $(2.612, 3.715)$

▶️ Answer/Explanation

Detailed solution

The condition requires finding the intervals where $E(t) > L(t)$ for $t \in [0, 5]$.
Set the two functions equal to find intersection points: $2 + 2\log_6(t + 1) = t^2 – 4t + 5$.
Using a graphing utility, the functions intersect at $t \approx 0.730$ and $t \approx 3.648$.
Test a value in the interval $(0.730, 3.648)$, such as $t = 2$.
$E(2) = 2 + 2\log_6(3) \approx 3.226$ and $L(2) = (2)^2 – 4(2) + 5 = 1$.
Since $3.226 > 1$, the rate of entry is greater throughout this middle interval.
Checking outside this interval shows $L(t) > E(t)$ for $t < 0.730$ and $t > 3.648$.
Therefore, the correct interval is $(0.730, 3.648)$, which corresponds to option (C).

Question

Let $f$ be a function with the property that for each time the input values increase by $1$, the output values double. If the function $g$ is the inverse of $f$, that is $g(x) = f^{-1}(x)$, then which of the following could be the graph of $y = g(x)$ in the $xy$-plane?

(A)

(B)

(C)

(D)

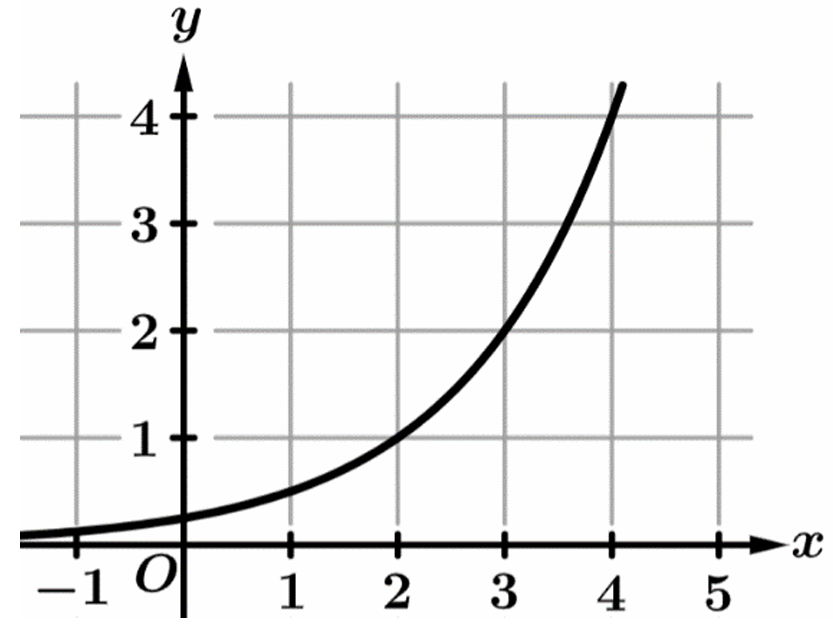
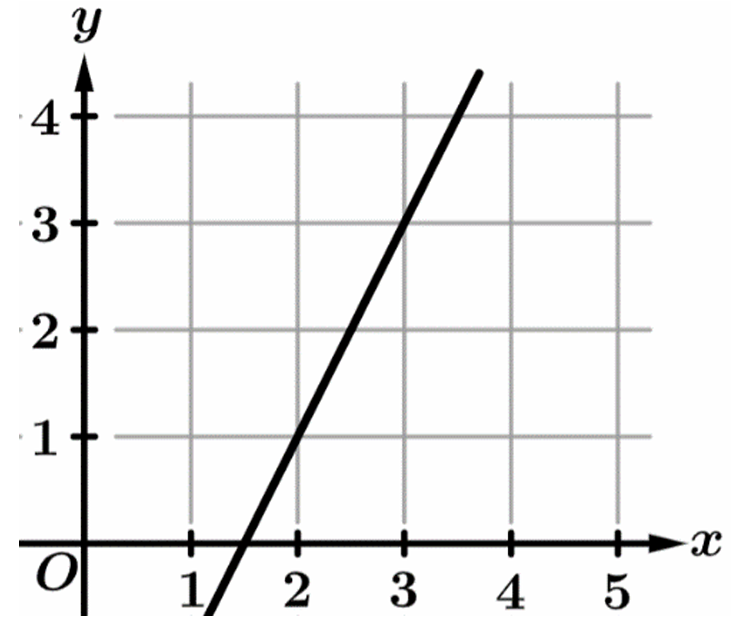
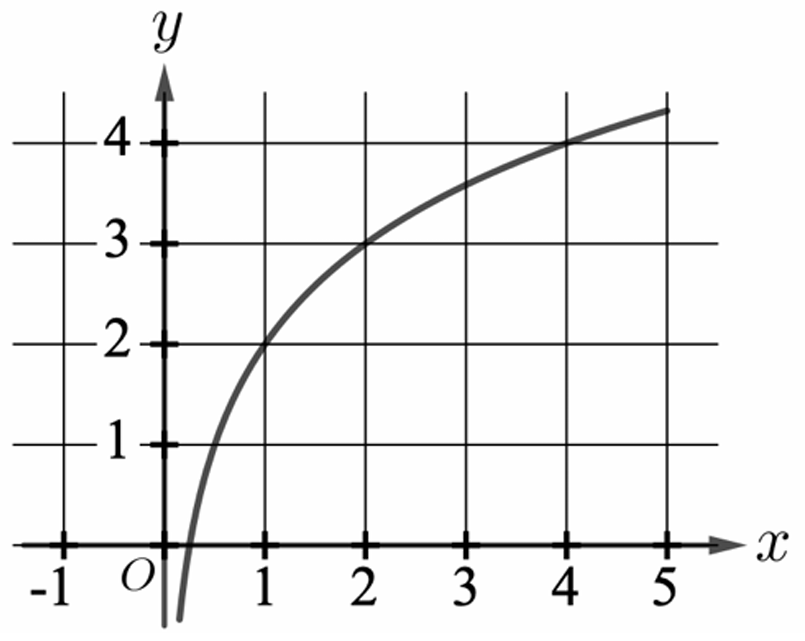
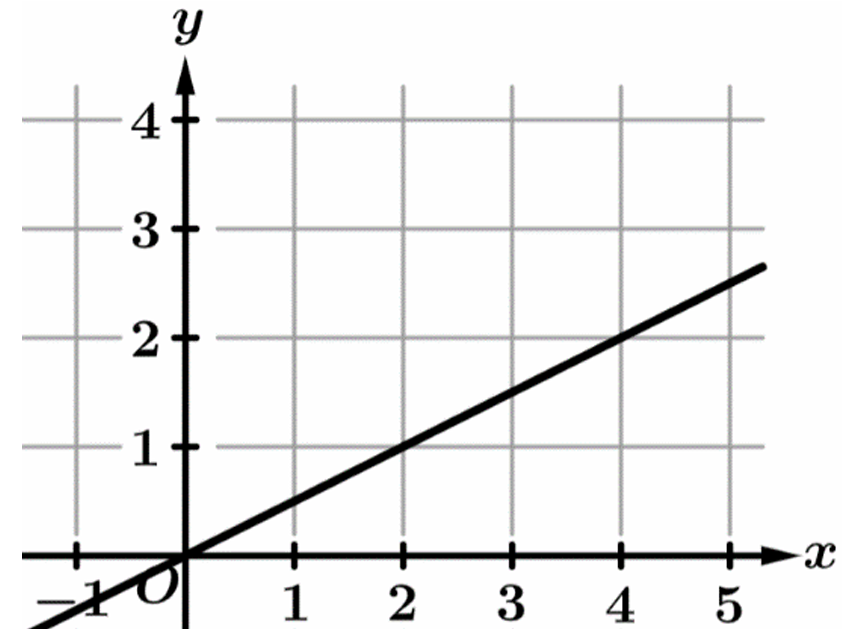
▶️ Answer/Explanation

Detailed solution

The property of $f$ describes an exponential function, specifically $f(x) = 2^x$.
Since $g(x)$ is the inverse of $f(x)$, it must be a logarithmic function, $g(x) = \log_{2}(x)$.
The graph of $y = \log_{2}(x)$ must pass through the point $(1, 0)$ because $\log_{2}(1) = 0$.
It must also pass through $(2, 1)$ and $(4, 2)$ because $2^1 = 2$ and $2^2 = 4$.
Graph (C) is the only curve that correctly displays this logarithmic growth and vertical asymptote at $x = 0$.
Graph (A) represents $f(x)$, while (B) and (D) are linear functions, which do not double per unit increase.

Question

The figures above show six data points plotted in the $xy$-plane, as well as the residual plot that results when the regression $M$ is used to model the given data. Which of the following statements about the regression model $M$ is best?

(A) The model $M$ is exponential, and the model was appropriate.
(B) The model $M$ is exponential, and the model was not appropriate.
(C) The model $M$ is logarithmic, and the model was appropriate.
(D) The model $M$ is logarithmic, and the model was not appropriate.

▶️ Answer/Explanation

Detailed solution

The scatter plot shows data points that increase rapidly at first and then level off, which is characteristic of a logarithmic shape.
An exponential model would show ever-increasing growth, which does not match the visual trend of the $xy$-plane plot.
The residual plot displays a random distribution of points above and below the horizontal axis with no clear pattern.
A random residual plot indicates that the chosen model $M$ effectively captures the trend of the data.
Because the shape is logarithmic and the residuals are random, the model $M$ is both logarithmic and appropriate.
Therefore, the best statement is (C).

Question

After a concert date is announced, tickets begin to sell online. The number of tickets remaining is modeled by the function $S(t) = 301.8 – 65.72 \ln(1.3t + 7)$, where $S$ is the number of tickets remaining $t$ hours after tickets begin selling online. At what time $t$ will there be $35$ tickets remaining?

(A) $29.254$
(B) $39.195$
(C) $41.495$
(D) $70.548$

▶️ Answer/Explanation

Detailed solution

Set the function equal to the remaining tickets: $35 = 301.8 – 65.72 \ln(1.3t + 7)$.
Subtract $301.8$ from both sides to get $-266.8 = -65.72 \ln(1.3t + 7)$.
Divide by $-65.72$ to isolate the natural log: $\ln(1.3t + 7) \approx 4.0596$.
Convert the logarithmic equation to exponential form: $1.3t + 7 = e^{4.0596}$.
Calculate the exponential value: $1.3t + 7 \approx 57.9536$.
Subtract $7$ from both sides: $1.3t \approx 50.9536$.
Divide by $1.3$ to find the time: $t \approx 39.195$.
The correct option is (B).

Question

After Mr. Passwater missed a day of school, a rumor began to spread that he had won the Powerball lottery and moved to Japan. Initially, seven students knew about the rumor (they were the ones that started it!). After two hours ($t=2$), a total of 15 students had heard the rumor. After six hours ($t=6$), 67 students had heard the rumor.

The number of students that have heard the rumor can be modeled by the piecewise function $R$ given by: $$R(t) = \begin{cases} 7(a)^{t/2} & \text{for } 0 \le t < 6 \\ -213.29 + b \ln t & \text{for } t \ge 6 \end{cases}$$ where $R(t)$ is the number of students that have heard the rumor at time $t$ hours since the rumor first began.

(A) (i) Use the given data to write two equations that can be used to find the values for constants $a$ and $b$ in the expression for $R(t)$.
(ii) Find the values for $a$ and $b$ as decimal approximations.

(B) (i) Use the given data to find the average rate of change in the number of students that have heard the rumor, in students per hour, from $t=2$ to $t=6$ hours. Express your answer as a decimal approximation. Show the computations that lead to your answer.
(ii) Interpret the meaning of your answer from (i) in the context of the problem.
(iii) Consider the values that result from using the average rate of change found in (i) to estimate the number of students that have heard the rumor for times $t=p$ hours, where $0 < p < 6$. Are these estimates less than or greater than the number of students predicted by the model $R$ for times $t=p$ hours? Explain your reasoning using characteristics of the average rate of change and characteristics of the model $R$.

(C) The model $R$ is valid for $0 \le t \le 12$ hours. Explain how the range values of the function $R$ should be limited by the context of the problem.

▶️ Answer/Explanation

Detailed solution

Part (A)

(i) Writing the equations:
We are given the following data points:
• At $t=2$, $R(2) = 15$.
• At $t=6$, $R(6) = 67$.

For $t=2$, since $0 \le 2 < 6$, we use the first part of the piecewise function: $R(t) = 7(a)^{t/2}$.
$$15 = 7(a)^{2/2} \quad \Rightarrow \quad 15 = 7a^1$$
Equation 1: $15 = 7a$

For $t=6$, since $t \ge 6$, we use the second part of the piecewise function: $R(t) = -213.29 + b \ln t$.
Equation 2: $67 = -213.29 + b \ln(6)$

(ii) Finding the values for $a$ and $b$:
From Equation 1:
$$a = \frac{15}{7} \approx 2.1428$$
From Equation 2:
$$67 + 213.29 = b \ln(6)$$
$$280.29 = b \ln(6)$$
$$b = \frac{280.29}{\ln(6)} \approx \frac{280.29}{1.79176} \approx 156.4328$$
Answer: $a \approx 2.143$, $b \approx 156.433$

Part (B)

(i) Average Rate of Change:
The formula for the average rate of change from $t=2$ to $t=6$ is:
$$\text{Avg Rate} = \frac{R(6) – R(2)}{6 – 2}$$
Substituting the given values ($R(6)=67$ and $R(2)=15$):
$$\text{Avg Rate} = \frac{67 – 15}{4} = \frac{52}{4} = 13$$
Answer: 13 students per hour.

(ii) Interpretation:
On average, the number of students who have heard the rumor increases by 13 students per hour between the 2nd hour and the 6th hour.

(iii) Estimates vs. Model Prediction:
Answer: The estimates are greater than the number of students predicted by the model.
Reasoning:
• On the interval $0 < t < 6$, the function $R(t) = 7(a)^{t/2}$ is an exponential growth function with a base greater than 1.
• Exponential growth functions are concave up (the rate of change is increasing).
• The average rate of change corresponds to the slope of the secant line connecting the points at $t=2$ and $t=6$.
• For a concave up curve, the secant line lies above the curve on the interval between the two points. Therefore, linear estimates based on the average rate (secant line) will be greater than the actual function values.

Part (C)

Explanation:
The range values (outputs) of $R(t)$ represent the number of students. In the context of the problem, this range must be limited in two ways:
1. Population Cap: The number of students who heard the rumor cannot exceed the total student population of the school.
2. Discrete Values: You cannot have a fraction of a student, so strictly speaking, the context implies the range should consist of whole numbers (non-negative integers).

Question

The Chinese bamboo tree exhibits a unique growth pattern. Once a seed has been planted, the Chinese bamboo tree does not break through the ground for several years. However, once it breaks through the ground, the Chinese bamboo tree grows exponentially. In one particular experiment, a group of biologists recorded the height of a Chinese bamboo tree once it broke through the ground. After one week ($t = 1$), the Chinese bamboo tree measured 3 feet, and after five weeks ($t = 5$), the same tree measured 89 feet.

The height of the Chinese bamboo tree can be modeled by the function $H$ given by $H(t) = ab^x$, where $H(t)$ is the height of the tree, in feet, $t$ weeks after it first breaks ground.

(A) (i) Use the given data to write two equations that can be used to find the values for constants $a$ and $b$ in the expression for $H(t)$.

(ii) Find the values for $a$ and $b$.

(B) (i) Use the given data to find the average rate of change of the height of the Chinese bamboo tree, in feet per week, from $t = 1$ to $t = 5$ weeks. Express your answer as a decimal approximation. Show the computations that lead to your answer.

(ii) Interpret the meaning of your answer from (i) in the context of the problem.

(iii) Consider the average rates of change of $H$ from $t = 5$ to $t = p$ weeks, where $p > 5$. Are these average rates of change less than or greater than the average rate of change from $t = 1$ to $t = 5$ weeks found in (i)? Explain your reasoning.

(C) For which $t$-value, $t = 4$ weeks or $t = 11$ weeks, should the biologists have more confidence in when using the model $H$? Give a reason for your answer in the context of the problem.

▶️ Answer/Explanation

Detailed solution

(A)(i) Equations
Substituting the points $(1, 3)$ and $(5, 89)$ into $H(t) = ab^t$:
1. $3 = ab^1$ (or $3 = ab$)
2. $89 = ab^5$

(A)(ii) Values for a and b
Dividing equation 2 by equation 1: $\frac{ab^5}{ab} = \frac{89}{3} \implies b^4 = 29.67$.
Solving for $b$: $b = (29.67)^{0.25} \approx 2.33$.
Solving for $a$: $a = \frac{3}{2.33} \approx 1.29$.

(B)(i) Average Rate of Change
$\text{Rate} = \frac{H(5) – H(1)}{5 – 1} = \frac{89 – 3}{4} = \frac{86}{4} = 21.5$
Answer: 21.5 feet per week.

(B)(ii) Interpretation
The answer indicates that between the first and fifth weeks, the bamboo tree grew at an average speed of 21.5 feet per week.

(B)(iii) Comparison
Greater. The function represents exponential growth ($b > 1$), which is concave up. This means the rate of growth increases over time, so the rate after week 5 will be steeper than the rate before week 5.

(C) Confidence
$t = 4$ weeks.
The biologists should be more confident in $t=4$ because it is an interpolation (within the observed data range). $t=11$ is an extrapolation; biological growth cannot remain exponential indefinitely, so the model is likely inaccurate that far out.

AP Precalculus -2.14 Logarithmic Function Modeling- MCQ Exam Style Questions - Effective Fall 2023