AP Precalculus -2.15 Semi-log Plots- MCQ Exam Style Questions - Effective Fall 2023
AP Precalculus -2.15 Semi-log Plots- MCQ Exam Style Questions – Effective Fall 2023
AP Precalculus -2.15 Semi-log Plots- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.
Question
(B) \( f(x) = x^2 \) and \( g(x) = 3x^2 \)
(C) \( f(x) = 2^x \) and \( g(x) = 3 \cdot 2^x \)
(D) \( f(x) = \ln(2x) \) and \( g(x) = 3 \ln(2x) \)
▶️ Answer/Explanation
A semi-log plot has a logarithmic scale on the vertical axis and a linear scale on the horizontal axis. Exponential functions \( y = k \cdot a^x \) appear as straight lines because \( \log y = \log k + x \log a \), which is linear in \( x \).
For \( f(x) = 2^x \) and \( g(x) = 3 \cdot 2^x \):
In a semi-log plot, \( \log f(x) = x \log 2 \) and \( \log g(x) = \log 3 + x \log 2 \).
Both are lines with slope \( \log 2 \), but different intercepts, so they appear as parallel lines.
✅ Answer: (C)
Question
(B) \( \frac{1}{10}t + 5 \)
(C) \( 2.5 \cdot 2^{(t/10)} \)
(D) \( 3 + 2^{(t/10)} \)
▶️ Answer/Explanation
A semi-log plot appears linear when the data follow an exponential model. In such a plot, a straight line corresponds to exponential growth of the form \( N(t) = a \cdot b^{t} \). The slope of the line in the semi-log plot relates to the growth factor over time.
Given the answer choice (C): \( N(t) = 2.5 \cdot 2^{(t/10)} \)
This means the population doubles every 10 days (since when \( t \) increases by 10, \( 2^{(t/10)} \) doubles). At \( t = 0 \), \( N(0) = 2.5 \) thousand, and at \( t = 10 \), \( N(10) = 2.5 \cdot 2 = 5 \) thousand, matching a point from the semi-log data if the plot is linear.
✅ Answer: (C)
Question
(B) Exponential growth
(C) Exponential decay
(D) Logarithmic
▶️ Answer/Explanation
1. Understand Semi-Log Plots:
A semi-log plot typically scales the \(y\)-axis logarithmically while keeping the \(x\)-axis linear. This is used to test for exponential relationships.
If the graph of \((\log y)\) versus \(x\) is a straight line, the original data follows an exponential model.
2. Analyze the Pattern:
The problem states the points follow a decreasing linear pattern on this plot. A linear pattern confirms the function is exponential.
The fact that it is decreasing (negative slope) indicates that as \(x\) increases, \(\log y\) decreases, which means \(y\) decreases toward 0.
3. Conclusion:
An exponential function with a negative rate of change corresponds to Exponential Decay.
✅ Answer: (C)
Question
▶️ Answer/Explanation
A semi‑log plot has a logarithmic vertical axis and linear horizontal axis. For an exponential function, the semi‑log plot appears linear.
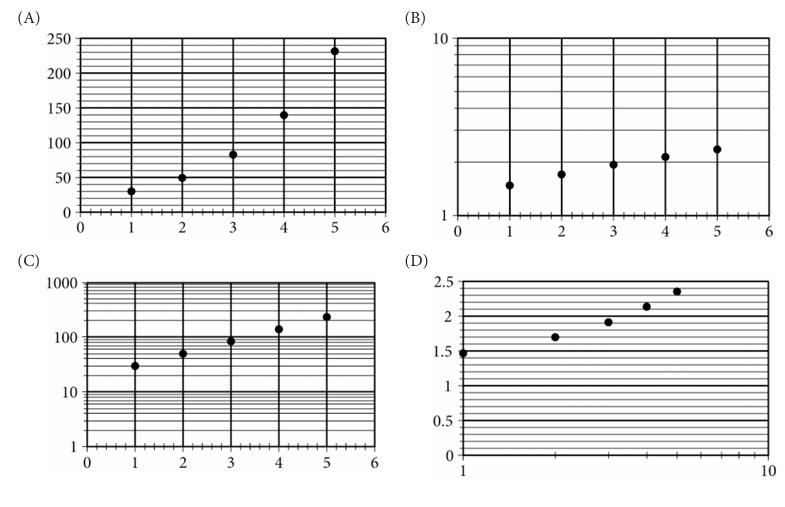
From the table: \( m(t) \) grows roughly by a constant factor (exponential). In a semi‑log plot, points \( (t, m(t)) \) are plotted with \( m(t) \) on a log scale.
Check values:
- log₁₀(30)≈1.48,
- log₁₀(50)≈1.70,
- log₁₀(83)≈1.92,
- log₁₀(139)≈2.14,
- log₁₀(231)≈2.36
increases roughly linearly in \( t \).
Graph C shows vertical axis labeled 1, 10, 100, 1000 (log scale) and likely shows points forming a straight line.
✅ Answer: (C)
Question
▶️ Answer/Explanation
The correct answer is (B).
The function is given by \( k(t) = 7 \cdot 5^t \).
A semi-log plot with a logarithmic vertical axis plots \( \ln(k(t)) \) against \( t \).
Taking the natural logarithm of both sides, we get \( \ln(k(t)) = \ln(7 \cdot 5^t) \).
Using the properties of logarithms, this expands to \( \ln(k(t)) = \ln 7 + \ln(5^t) \).
This simplifies further to \( \ln(k(t)) = (\ln 5)t + \ln 7 \).
This equation is in the linear form \( y = mx + c \), where the slope \( m = \ln 5 \).
Therefore, the data appear linear with a slope of \( \ln 5 \).
Question
▶️ Answer/Explanation
The correct option is (B).
In a semi-log plot with a natural log scale, we transform the output as $y = \ln(k(t))$.
Substituting the given function: $y = \ln(7 \cdot 5^t)$.
Using log properties, this expands to $y = \ln 7 + \ln(5^t)$.
Applying the power rule: $y = \ln 7 + t \cdot \ln 5$.
This matches the linear form $y = mx + b$, where the variable is $t$.
The slope $m$ of this linear relationship is $\ln 5$.
Question
(B) $f(x) = x^{2}$ and $g(x) = 3x^{2}$
(C) $f(x) = 2^{x}$ and $g(x) = 3 \cdot 2^{x}$
(D) $f(x) = \ln(2x)$ and $g(x) = 3 \ln(2x)$
▶️ Answer/Explanation
In a semi-log plot, the vertical axis is logarithmic, so we plot $Y = \log(f(x))$.
For functions to appear linear, they must be of the form $y = Ab^{x}$, since $\log(Ab^{x}) = \log(A) + x\log(b)$.
For lines to be parallel, they must have the same slope in the log-transformed state.
In option (C), let $f(x) = 2^{x}$ and $g(x) = 3 \cdot 2^{x}$.
Applying log: $Y_{1} = \log(2^{x}) = x \log(2)$ and $Y_{2} = \log(3 \cdot 2^{x}) = \log(3) + x \log(2)$.
Both equations have the same slope, $\log(2)$, making them parallel lines.
Therefore, the correct choice is (C).
Question
▶️ Answer/Explanation
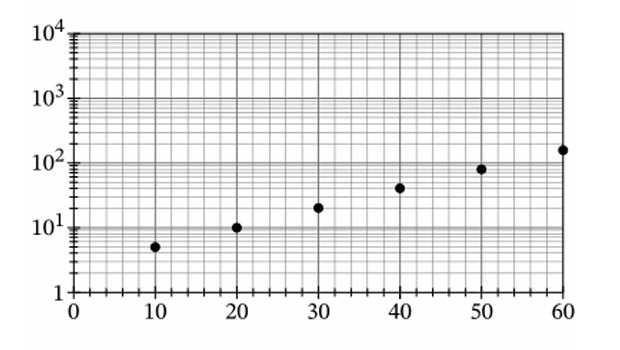
The plot is semi-logarithmic, where a linear trend indicates an exponential function.
At $t = 20$, the point on the graph is at $10^1$, which means $N(20) = 10$.
At $t = 50$, the point is just below $10^2$ (roughly $80$); checking option (C): $2.5 \cdot 2^{(50/10)} = 2.5 \cdot 32 = 80$.
Testing option (C) for $t = 20$ gives $2.5 \cdot 2^{(20/10)} = 2.5 \cdot 4 = 10$, matching the data exactly.
Options (A) and (B) are linear functions, which would appear curved on a semi-log scale.
Option (D) at $t = 20$ yields $3 + 2^2 = 7$, which does not match the observed value of $10$.
Therefore, the function that correctly defines the data is (C).
Question (Calc allowed)
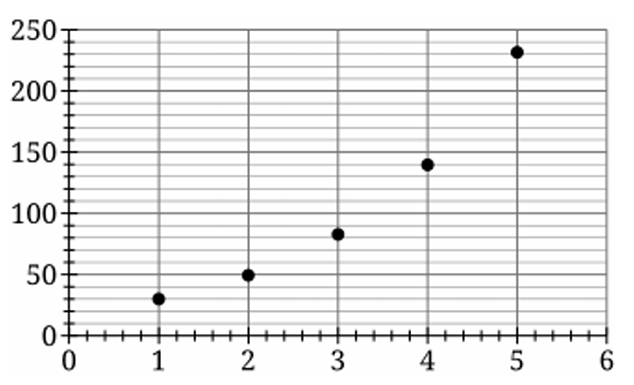
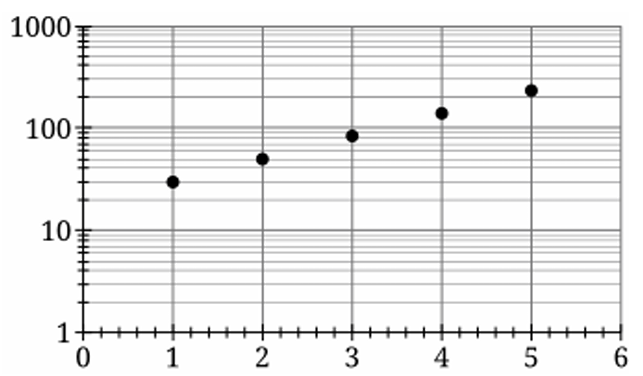
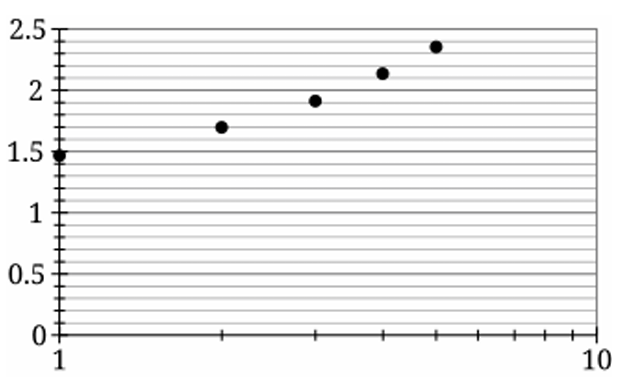
▶️ Answer/Explanation
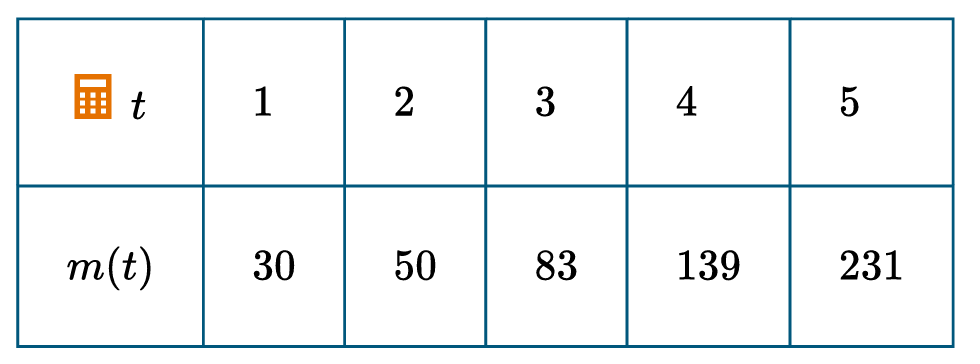
The correct graph is (C).
A semi-log plot uses a logarithmic scale for the vertical axis to linearize exponential data.
The data values for $m(t)$ range from $30$ to $231$.
The vertical axis must include the interval $[30, 231]$, which fits within the $10$ to $1000$ scale.
The constant ratio $\frac{m(t+1)}{m(t)} \approx 1.67$ indicates the function is exponential.
On a logarithmic scale, this exponential relationship appears as a straight line.
Graph (C) shows the points forming a linear pattern on a log-scaled $y$-axis.
Question
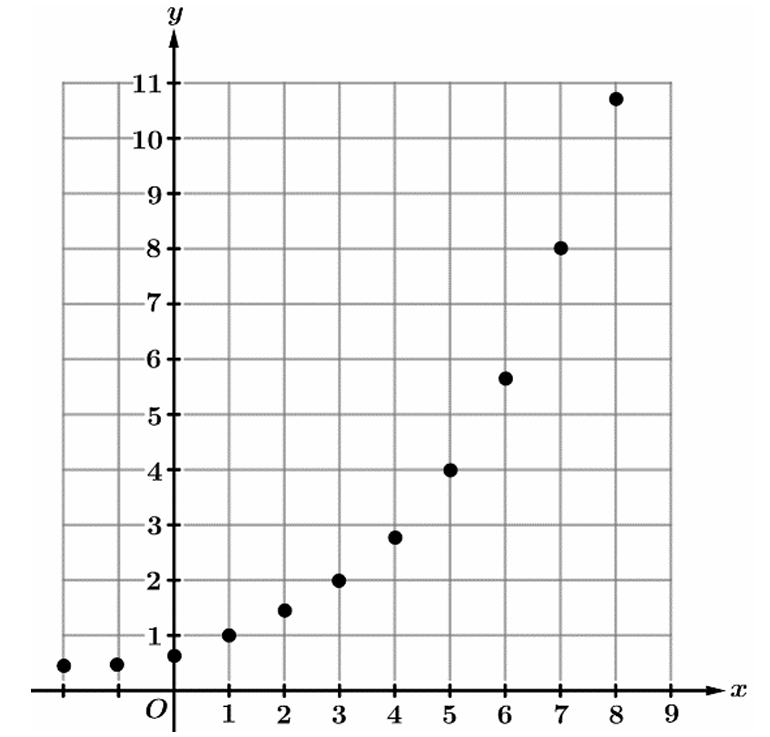
(B) The data show no apparent pattern, because only logarithmic data will display a pattern when graphed on a semi-log plot in which the vertical axis is logarithmically scaled.
(C) The data will appear exponential, because data whose outputs increase multiplicatively while the inputs increase additively display an exponential pattern when graphed on a semi-log plot in which the vertical axis is logarithmically scaled.
(D) The data will appear logarithmic, because data that exhibit exponential behavior in the \( xy \)-plane display a logarithmic pattern when graphed on a semi-log plot in which the vertical axis is logarithmically scaled.
▶️ Answer/Explanation
The correct option is (A).
The graphed points show that as \( x \) increases linearly, \( y \) increases by a constant ratio (doubling).
This identifies the function \( f \) as an exponential relationship of the form \( y = a \cdot b^x \).
On a semi-log plot, the vertical axis represents \( \log(y) \) instead of \( y \).
Applying a logarithm to both sides gives \( \log(y) = \log(a) + x \log(b) \).
This equation follows the linear form \( Y = mx + c \), where \( Y = \log(y) \).
Thus, exponential data always appears as a straight line on a semi-logarithmic scale.
Question
▶️ Answer/Explanation
The correct answer is (A).
On a semi-log plot, a straight line represents an exponential function of the form $f(x) = ab^x$.
Observing the y-intercept at $x = 0$, the value is slightly below $1000$, which matches the initial value $a = 800$.
As $x$ increases, the $y$ values decrease, indicating an exponential decay where the base $b$ must be less than $1$.
At $x = 1$, the point is at $400$, which satisfies $800 \left( \frac{1}{2} \right)^1 = 400$.
At $x = 3$, the point is at $100$, which satisfies $800 \left( \frac{1}{2} \right)^3 = 800 \cdot \frac{1}{8} = 100$.
Option (C) is linear and (D) is logarithmic, neither of which produces a straight line on a semi-log scale.
Question
▶️ Answer/Explanation
The correct answer is (A) $-\ln 5$.
In a semi-log plot with a natural log scale, the vertical coordinate is $y = \ln(g(x))$.
Substitute the function: $y = \ln\left( 6 \cdot \left( \frac{1}{5} \right)^x \right)$.
Use log properties: $y = \ln 6 + \ln\left( \left( \frac{1}{5} \right)^x \right)$.
Bring down the exponent: $y = \ln 6 + x \ln\left( \frac{1}{5} \right)$.
Apply the division rule for logs: $y = \ln 6 + x(\ln 1 – \ln 5)$.
Since $\ln 1 = 0$, the linear equation becomes $y = (-\ln 5)x + \ln 6$.
The slope of this linear relationship is the coefficient of $x$, which is $-\ln 5$.
Question
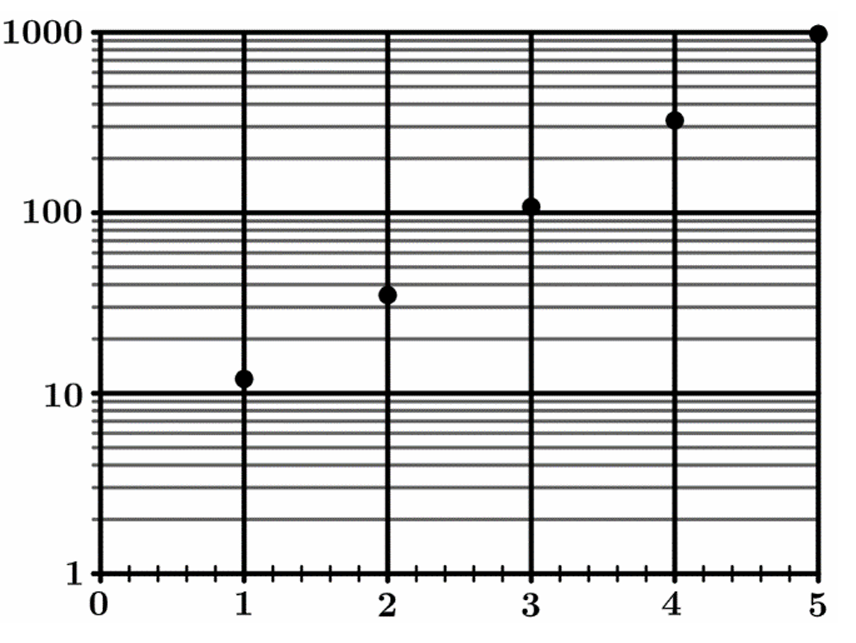
▶️ Answer/Explanation
The correct option is (D).
A semi-log plot uses a logarithmic scale for the vertical axis, where increments represent powers of $10$.
In Graph D, the y-axis labels are $1, 10, 100, 1000$, which indicates a $\log_{10}$ scale.
Plotting the data: at $x=1, f(x)=12$ is just above $10$.
At $x=3, f(x)=108$ is just above $100$.
At $x=5, f(x)=980$ is just below $1000$.
These points form a nearly straight line on the semi-log grid, characteristic of exponential growth.
Question
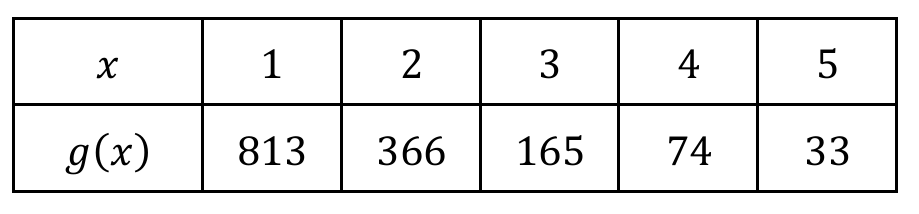
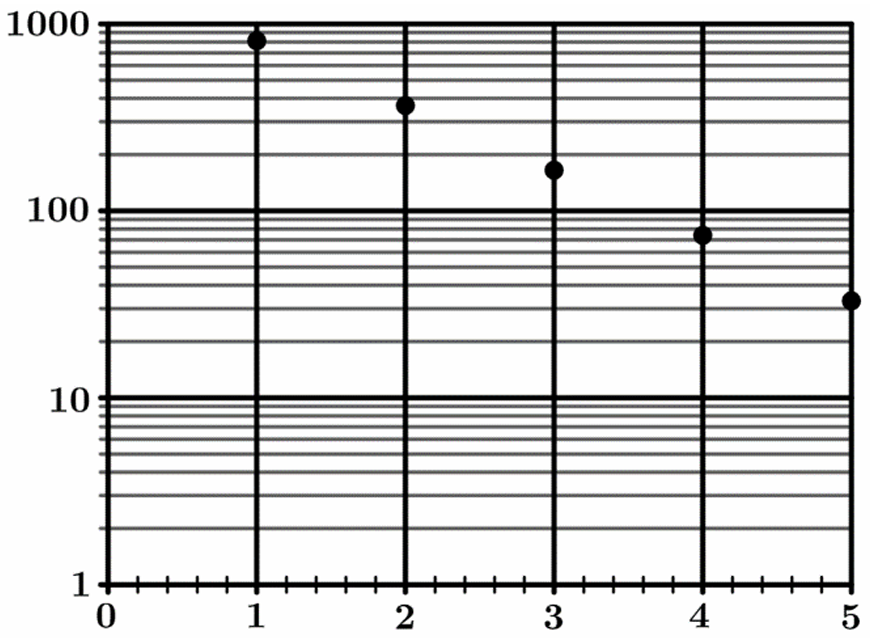
▶️ Answer/Explanation
The correct answer is (A).
The values of \(g(x)\) decrease by a constant factor of approximately \(0.45\), indicating an exponential function.
In a semi-log plot, an exponential function \(g(x) = ab^x\) appears as a straight line.
The vertical axis in Graph A uses a base-\(10\) logarithmic scale spanning from \(10^0\) to \(10^3\).
Point \((1, 813)\) is correctly placed near the top grid line of \(1000\).
Point \((5, 33)\) is correctly placed between \(10\) and \(100\).
The linear alignment of points in Graph A confirms the relationship \(\log(g(x)) = \log(a) + x\log(b)\).
Options (B), (C), and (D) are incorrect due to improper scaling or the use of linear axes.
Question
| \(x\) | \(h(x)\) |
|---|---|
| \(5\) | \(2\) |
| \(10\) | \(6\) |
| \(15\) | \(18\) |
| \(20\) | \(54\) |
| \(25\) | \(162\) |
(B) The data would appear linear using a semi-log plot, because the function \(h\) is best modeled using an exponential function.
(C) The data would appear logarithmic using a semi-log plot, because the function \(h\) is best modeled using an exponential function.
(D) The data would appear logarithmic using a semi-log plot, because the function \(h\) is best modeled using a logarithmic function.
▶️ Answer/Explanation
The correct answer is (B).
Observe that as \(x\) increases by a constant amount of \(5\), the value of \(h(x)\) is multiplied by a constant factor of \(3\).
This constant ratio (\(6/2 = 3\), \(18/6 = 3\), etc.) indicates that \(h(x)\) is an exponential function.
An exponential function is defined by the general form \(y = ab^x\).
Taking the logarithm of both sides gives \(\log(y) = \log(a) + x\log(b)\).
This transformation shows a linear relationship between \(x\) and \(\log(y)\).
Therefore, on a semi-log plot with a logarithmic vertical axis, the data will appear as a straight line.
Question
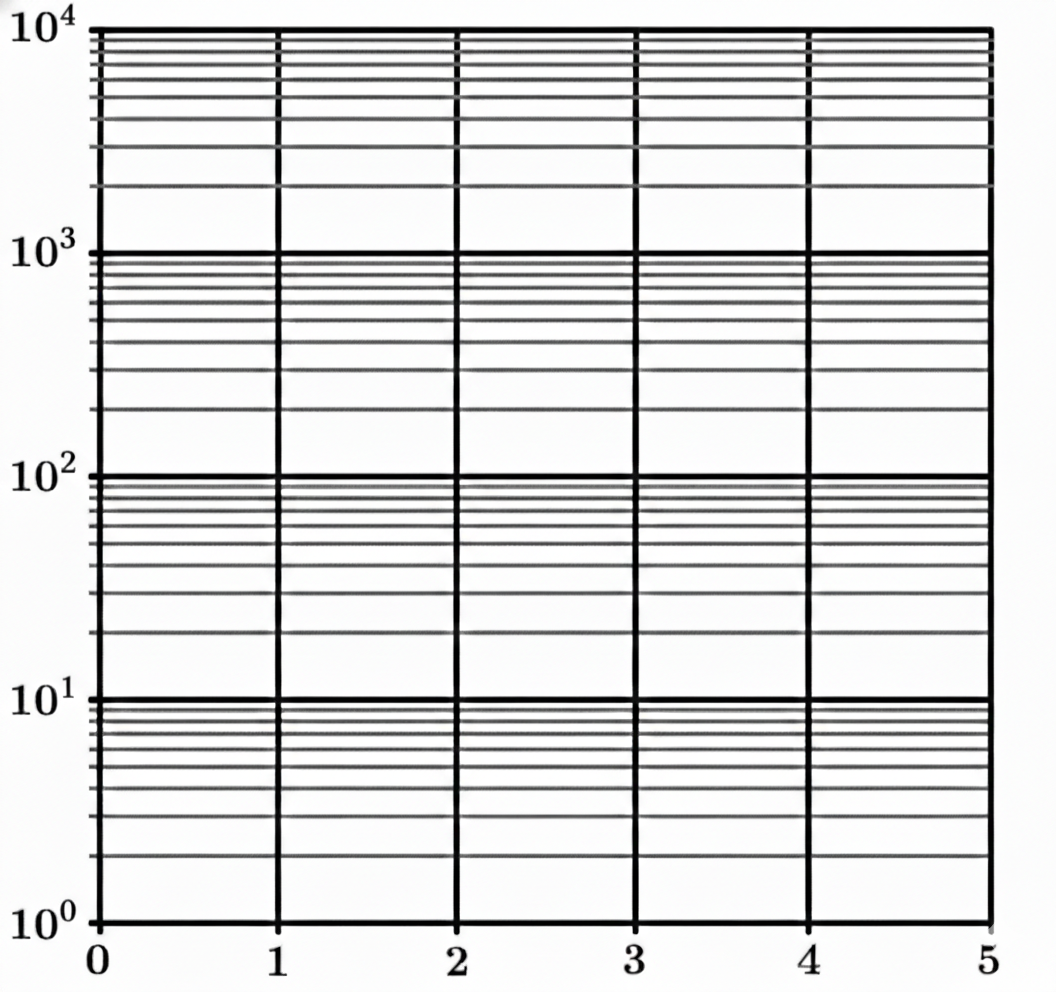
(B) The data appear logarithmic and concave up.
(C) The data appear exponential and concave down.
(D) The data appear logarithmic and concave down.
▶️ Answer/Explanation
The correct option is (A).
A straight line on a semi-log plot indicates an exponential relationship between $x$ and $y$.
The linear trend follows the form $\log_{10}(y) = mx + b$, which simplifies to $y = 10^{mx+b}$.
Since the slope $m$ is positive, the data represents exponential growth.
In a standard $xy$-plane, the rate of change of an exponential growth function increases as $x$ increases.
This increasing slope results in a graph that is concave up.
Logarithmic functions, by contrast, would appear linear on a log-log plot or semi-log $x$ plot.
Question
(B) $f(x) = 5 \cdot 2^x$
(C) $f(x) = 2 + 5^x$
(D) $f(x) = 5 + 2^x$
▶️ Answer/Explanation
In a semi-log plot with a logarithmic vertical axis, the linear equation is written as $\log_{10}(f(x)) = y$.
Substitute the given linear model: $\log_{10}(f(x)) = (\log_{10} 2)x + \log_{10} 5$.
Apply the power property of logarithms: $\log_{10}(f(x)) = \log_{10}(2^x) + \log_{10} 5$.
Apply the product property of logarithms: $\log_{10}(f(x)) = \log_{10}(5 \cdot 2^x)$.
Take the antilogarithm of both sides: $f(x) = 5 \cdot 2^x$.
This matches option (B).
Question
▶️ Answer/Explanation
The semi-log plot represents the relationship as $y = \ln(g(x))$.
Given the linear model: $y = \ln 4 – x(\ln 3)$.
Substitute $y$ with $\ln(g(x))$ to get: $\ln(g(x)) = \ln 4 – \ln(3^x)$.
Apply logarithm rules to combine terms: $\ln(g(x)) = \ln\left(\frac{4}{3^x}\right)$.
Exponentiate both sides to solve for $g(x)$: $g(x) = 4 \cdot \left(\frac{1}{3}\right)^x$.
Compare this to the standard form $g(x) = ab^x$.
The constant $b$ is identified as $\frac{1}{3}$.
Thus, the correct option is (D).
Question

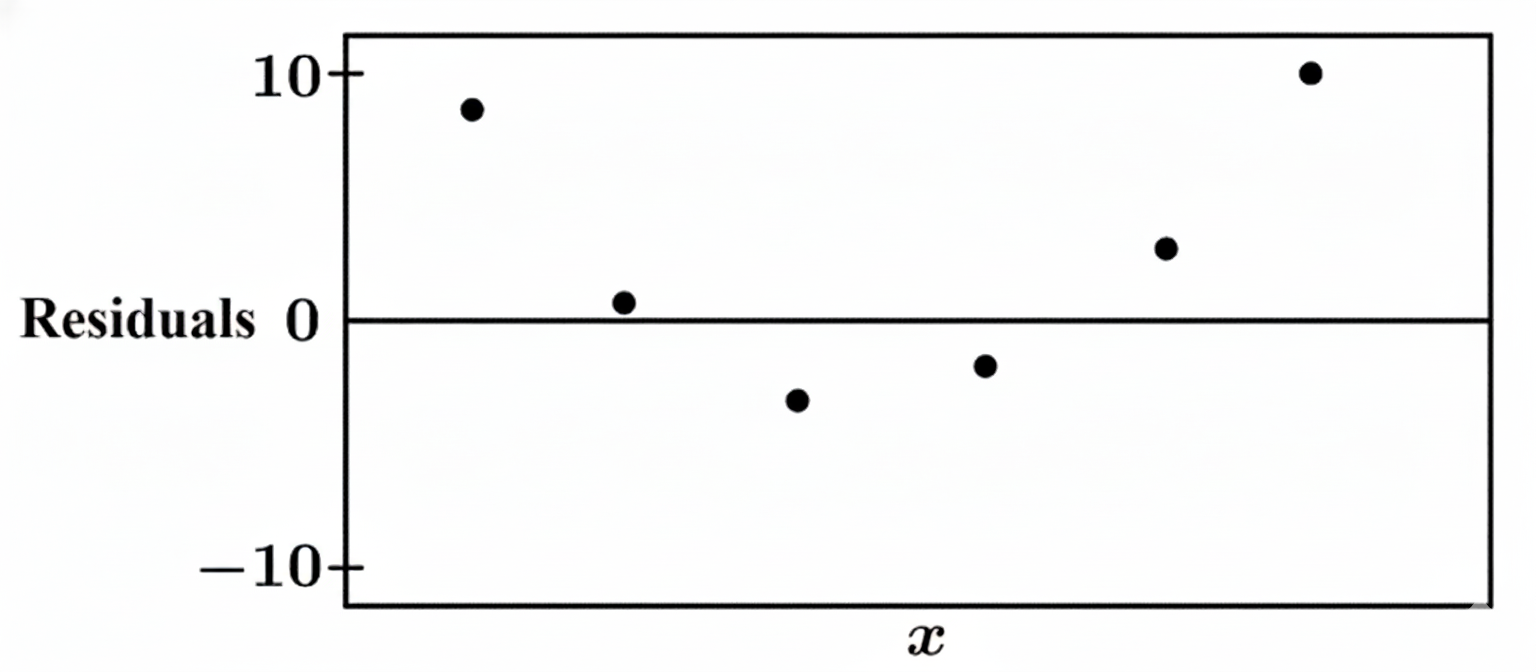
(B) The model \(P\) is linear, and the model was not appropriate.
(C) The model \(P\) is exponential, and the model was appropriate.
(D) The model \(P\) is exponential, and the model was not appropriate.
▶️ Answer/Explanation
The correct option is (C).
A straight line on a semi-log plot indicates an exponential relationship between variables.
Since the data points follow a linear trend on the \(\log\) scale, model \(P\) must be exponential.
The residual plot shows points randomly scattered around the zero line with no discernible pattern.
A random residual plot confirms that the chosen regression model is appropriate for the data.
Therefore, model \(P\) is exponential and the fit is considered appropriate.