AP Precalculus -2.15 Semi-log Plots- Study Notes - Effective Fall 2023
AP Precalculus -2.15 Semi-log Plots- Study Notes – Effective Fall 2023
AP Precalculus -2.15 Semi-log Plots- Study Notes – AP Precalculus- per latest AP Precalculus Syllabus.
LEARNING OBJECTIVE
Determine if an exponential model is appropriate by examining a semi-log plot of a data set
Construct the linearization of exponential data.
Key Concepts:
Semi-Log Plots and Exponential Behavior
Advantage of Semi-Log Plots for Exponential Models
Applying Linear Modeling Techniques to Semi-Log Graphs
Linear Models from Exponential Functions on Semi-Log Plots
Semi-Log Plots and Exponential Behavior
A semi-log plot is a graph in which one axis is scaled logarithmically while the other axis remains on a standard linear scale.
When the y-axis is logarithmically scaled and the x-axis is linear, functions or data sets that demonstrate exponential behavior appear as straight lines.
This occurs because exponential functions have the form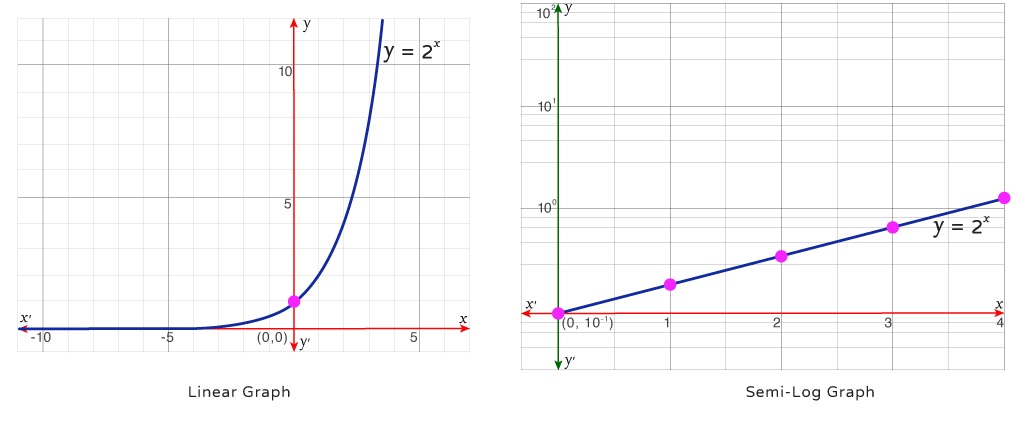
\( \mathrm{ \displaystyle y=ab^x } \)
Taking the logarithm of the output gives
\( \mathrm{ \displaystyle \log y=\log a + x\log b } \)
This equation is linear in \( \mathrm{x} \), which explains why exponential data form a straight line on a semi-log plot.
Key Interpretation
• Straight line on a semi-log plot ⇒ exponential relationship
• Slope represents the growth or decay factor
• Intercept relates to the initial value
Example
A population follows the model
\( \mathrm{ \displaystyle y=500(1.2)^x } \)
Explain how this model would appear on a semi-log plot with a logarithmic y-axis.
▶️ Answer/Explanation
Taking logarithms gives
\( \mathrm{ \displaystyle \log y=\log 500 + x\log 1.2 } \)
This is a linear equation in \( \mathrm{x} \), so the graph appears as a straight line on the semi-log plot.
Conclusion
The straight-line pattern confirms exponential growth.
Example
A data set appears curved on a standard graph but forms a straight line when plotted on a semi-log plot with a logarithmic y-axis.
What does this indicate about the relationship between the variables?
▶️ Answer/Explanation
A straight line on a semi-log plot indicates that the logarithm of the output changes linearly with the input.
Conclusion
The variables have an exponential relationship.
Advantage of Semi-Log Plots for Exponential Models
One major advantage of using semi-log plots is that a constant does not need to be added to the dependent variable values in order to reveal an exponential relationship.
For exponential data modeled by
\( \mathrm{ \displaystyle y=ab^x } \)
taking the logarithm of the dependent variable naturally transforms the relationship into a linear one:
\( \mathrm{ \displaystyle \log y=\log a + x\log b } \)
Because the logarithmic scale directly accounts for proportional change, vertical shifts of the data are unnecessary to detect exponential behavior.
Key Benefit
• Exponential patterns become linear without modifying the data
• Simplifies model selection and interpretation
• Preserves the original meaning of the dependent variable
Example
A data set shows rapid early growth followed by slower growth. On a standard graph, the data do not clearly follow a simple curve.
Explain why plotting the data on a semi-log plot is advantageous.
▶️ Answer/Explanation
A semi-log plot removes the need to adjust the data by adding constants.
If the data follow an exponential pattern, they will appear as a straight line.
Conclusion
This makes it easier to confirm whether an exponential model is appropriate.
Example
Two data sets are being analyzed for exponential behavior. One requires adding a constant to reveal proportional change, while the other is plotted on a semi-log plot.
Explain why the semi-log plot approach is preferred.
▶️ Answer/Explanation
Semi-log plots reveal exponential patterns directly without altering the dependent variable.
Conclusion
This preserves the integrity of the data and simplifies analysis.
Applying Linear Modeling Techniques to Semi-Log Graphs
A key advantage of semi-log graphs is that techniques used to model linear functions can be directly applied when analyzing exponential data.
When the y-axis is logarithmically scaled, an exponential relationship of the form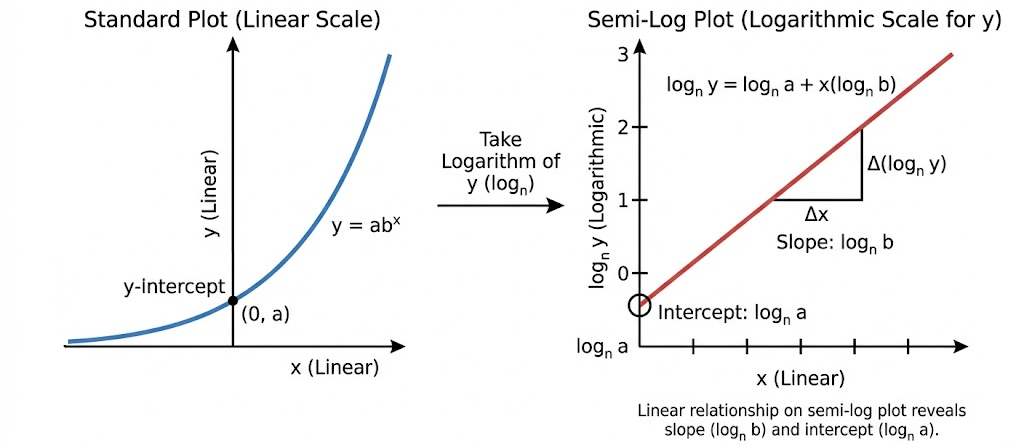
\( \mathrm{ \displaystyle y=ab^x } \)
appears as a straight line on the semi-log graph because
\( \mathrm{ \displaystyle \log y=\log a + x\log b } \)
This linear relationship allows the same methods used for linear models to be applied, including:
• estimating slope using two points
• interpreting slope as a rate of change
• using linear regression and residual plots
In this context, the slope of the line represents the logarithm of the growth or decay factor, and the intercept relates to the initial value.
Example
A data set appears as a straight line on a semi-log plot with a logarithmic y-axis.
Explain how the slope of the line is interpreted.
▶️ Answer/Explanation
Because the graph is linear on a semi-log plot, the slope can be found using two points, just as in linear modeling.
The slope represents \( \mathrm{\log b} \), where \( \mathrm{b} \) is the exponential growth or decay factor.
Conclusion
A constant slope on a semi-log plot indicates a constant multiplicative rate of change.
Example
A researcher fits a straight line to data on a semi-log plot and finds no visible pattern in the residuals.
What does this indicate about the model?
▶️ Answer/Explanation
A residual plot with no pattern indicates that the linear fit on the semi-log graph is appropriate.
This confirms that the original data follow an exponential model.
Conclusion
Linear modeling techniques validate exponential relationships when applied to semi-log graphs.
Linear Models from Exponential Functions on Semi-Log Plots
An exponential model of the form
\( \mathrm{ \displaystyle y=ab^x } \)
can be rewritten as a linear model when the dependent variable is plotted on a logarithmic scale.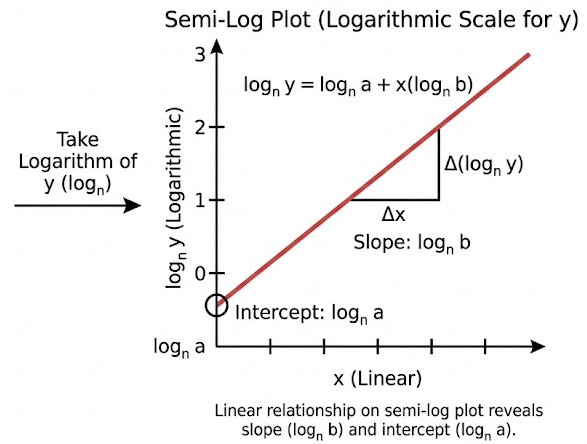
Taking the logarithm with base \( \mathrm{n} \), where \( \mathrm{n>0} \) and \( \mathrm{n\ne1} \), gives
\( \mathrm{ \displaystyle \log_n y=\log_n a + x\log_n b } \)
On a semi-log plot, this relationship appears as a straight line with:
• linear rate of change (slope): \( \mathrm{\log_n b} \)
• initial linear value (intercept): \( \mathrm{\log_n a} \)
Thus, exponential growth or decay in the original model corresponds to a constant slope in the semi-log representation.
Example
Given the exponential model
\( \mathrm{ \displaystyle y=200(1.5)^x } \)
write the corresponding linear model for a semi-log plot using base 10.
▶️ Answer/Explanation
Take the logarithm base 10 of both sides:
\( \mathrm{ \displaystyle \log_{10} y=\log_{10}200 + x\log_{10}1.5 } \)
This is a linear equation of the form \( \mathrm{y=mx+c} \) on the semi-log plot.
Conclusion
The slope is \( \mathrm{\log_{10}1.5} \), and the intercept is \( \mathrm{\log_{10}200} \).
Example
A straight line on a semi-log plot has slope \( \mathrm{\log_{10}2} \) and intercept \( \mathrm{\log_{10}50} \).
Determine the corresponding exponential model.
▶️ Answer/Explanation
From the linear form:
\( \mathrm{ \displaystyle \log_{10} y=(\log_{10}2)x+\log_{10}50 } \)
Rewrite in exponential form:
\( \mathrm{ \displaystyle y=50\cdot2^x } \)
Conclusion
The exponential model has initial value 50 and growth factor 2.
