AP Precalculus -2.2 Linear and Exponential Change- MCQ Exam Style Questions - Effective Fall 2023

AP Precalculus -2.2 Linear and Exponential Change- MCQ Exam Style Questions – Effective Fall 2023

AP Precalculus -2.2 Linear and Exponential Change- MCQ Exam Style Questions – AP Precalculus- per latest AP Precalculus Syllabus.

AP Precalculus – MCQ Exam Style Questions- All Topics

Question

Which of the following tables provides evidence that $ f $ is an exponential function if $ y = f(x) $?

(A) \[\begin{array}{c|c} x & y \\ \hline 1 & 3 \\ 2 & 6 \\ 3 & 9 \\ 4 & 12 \\ \end{array}\]
(B) \[\begin{array}{c|c} x & y \\ \hline 5 & 30 \\ 6 & 42 \\ 7 & 56 \\ 8 & 72 \\ \end{array}\]
(C) \[\begin{array}{c|c} x & \ln y \\ \hline 1 & 1 \\ 2 & 3 \\ 3 & 9 \\ 4 & 27 \\ \end{array}\]
(D) \[\begin{array}{c|c} x & \ln y \\ \hline 5 & 50 \\ 6 & 60 \\ 7 & 70 \\ 8 & 80 \\ \end{array}\]

▶️ Answer/Explanation

Detailed solution

A function is exponential if the natural logarithm of its output values $ \ln y $ is linear in $ x $.
In option (C), $ \ln y $ values are 1, 3, 9, 27 — these are not linear in $ x $.
In option (D), $ \ln y $ values are 50, 60, 70, 80 — these form an arithmetic sequence, so $ \ln y $ is linear in $ x $.
Thus $ y = e^{mx+b} $ is exponential.
✅ Answer: (D)

Question

The function $ g $ is a function of the form $ g(x) = a \cdot b^x $, where $ a \neq 0 $ and $ b > 0 $. The function $ f $ is given by $ f(x) = g(x) + 4 $. Which of the following statements is true?

(A) The output values of both $ f $ and $ g $ are proportional over equal-length input-value intervals.
(B) The output values of $ f $ only, not $ g $, are proportional over equal-length input-value intervals.
(C) The output values of $ g $ only, not $ f $, are proportional over equal-length input-value intervals.
(D) The output values of neither $ f $ nor $ g $ are proportional over equal-length input-value intervals.

▶️ Answer/Explanation

Detailed solution

Exponential functions $ g(x) = a \cdot b^x $ have outputs that are proportional over equal-length input intervals (ratio constant).
Adding a constant $ +4 $ to $ g $ gives $ f(x) $, which is no longer a pure exponential; its successive ratios are not constant.
Thus only $ g $ has proportional output changes over equal-length input intervals.
✅ Answer: (C)

Question

The number of students at Speedway High School that earn a qualifying score on an AP math exam can be modeled using an arithmetic sequence, where Mr. Passwater’s first year at SHS is year 1. The number of students earning a qualifying score in year 3 was 52, and the number of students earning a qualifying score in year 6 was 61. Which of the following functions gives the number of students earning a qualifying score in year $t$, where $t$ is a whole number?

(A) $ f(t) = \frac{1}{3}t + 51 $

(B) $ g(t) = 3t + 43 $

(D) $ k(t) = 3t + 61 $

▶️ Answer/Explanation

Detailed solution

The problem provides two data points for an arithmetic sequence (linear model): $(3, 52)$ and $(6, 61)$.

Step 1: Calculate the common difference (slope, $d$) using the two points: $d = \frac{61 – 52}{6 – 3} = \frac{9}{3} = 3$.

Step 2: The function is linear, so it takes the form $y = dt + b$. Substitute $d=3$.

Step 3: Use the point $(3, 52)$ to solve for the constant $b$: $52 = 3(3) + b \rightarrow 52 = 9 + b$.

Step 4: Solving for $b$ gives $b = 52 – 9 = 43$.

Step 5: The final function is $g(t) = 3t + 43$. This matches option (B).

Question

(Calculator Active) Fearing a new computer virus, a security company performs a simulation to predict the number of computers that might be affected by the virus. The number of infected computers can be modeled by a geometric sequence, where the first day of the simulation is day $1$. On day $6$, the virus had infected $750$ computers, and on day $10$ the virus had infected $3200$ computers. To the nearest whole number, how many computers had been infected by the virus on day $14$ based on the simulation?

(A) $5,650$

(B) $5,717$

(D) $120,329$

▶️ Answer/Explanation

Detailed solution

The problem describes a geometric sequence where the term $g_n$ represents the number of infected computers on day $n$.
We are given $g_6 = 750$ and $g_{10} = 3200$.
Using the property of geometric sequences, we can relate terms using the common ratio $r$: $g_{10} = g_6 \cdot r^{(10-6)}$.
Substitute the known values: $3200 = 750 \cdot r^4$.
Solving for $r^4$ gives: $r^4 = \frac{3200}{750}$.
We need to find $g_{14}$, which can be expressed as: $g_{14} = g_{10} \cdot r^{(14-10)} = 3200 \cdot r^4$.
Substituting the value of $r^4$: $g_{14} = 3200 \cdot \left(\frac{3200}{750}\right) = 13653.33\dots$
Rounding to the nearest whole number, the number of infected computers is $13,653$.
The correct option is (C).

Question

Which of the following tables provides evidence that $f$ is an exponential function if $y = f(x)$?

(A)

$x$	$y$
$1$	$3$
$2$	$6$
$3$	$9$
$4$	$12$

(B)

$x$	$y$
$5$	$30$
$6$	$42$
$7$	$56$
$8$	$72$

(C)

$x$	$\ln y$
$1$	$1$
$2$	$3$
$3$	$9$
$4$	$27$

(D)

$x$	$\ln y$
$5$	$50$
$6$	$60$
$7$	$70$
$8$	$80$

▶️ Answer/Explanation

Detailed solution

An exponential function $y = a \cdot b^x$ becomes linear when transformed by logarithms.
Applying the natural log gives the equation $\ln y = \ln a + x \ln b$.
This implies that for an exponential function, $\ln y$ must have a constant rate of change relative to $x$.
In Table (D), as $x$ increases by $1$ unit, $\ln y$ increases by a constant addition of $10$.
Table (A) shows a linear relationship for $y$ itself, not an exponential one.
Table (C) shows $\ln y$ growing exponentially, which would mean $y$ grows even faster.
Only Table (D) shows the constant slope for $\ln y$ that characterizes an exponential function $f(x)$.
Thus, the correct choice is Table (D).

Question

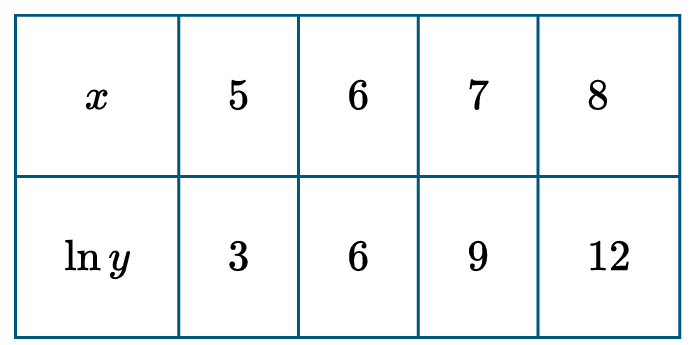
The table gives ordered pairs $(x, \ln y)$. For the function $y = f(x)$, which of the following statements about $f$ is supported by the data in the table?

(A) The function $f$ is logarithmic because the values of $x$ and the values of $\ln y$ both form arithmetic sequences.
(B) The function $f$ is linear because the values in each column form an arithmetic sequence.
(C) The function $f$ is exponential because the values of $x$ and the values of $\ln y$ both form arithmetic sequences.
(D) The function $f$ is exponential because the values of $\ln y$ increase faster than the values of $x$.

▶️ Answer/Explanation

Detailed solution

The $x$ values increase by a constant $1$ ($5, 6, 7, 8$), forming an arithmetic sequence.
The $\ln y$ values increase by a constant $3$ ($3, 6, 9, 12$), forming an arithmetic sequence.
Since $\ln y$ is a linear function of $x$, the relationship is of the form $\ln y = mx + b$.
Applying the exponential to both sides gives $y = e^{mx + b}$, which simplifies to $y = Ab^x$.
This structure confirms that the function $f(x)$ is an exponential function.
Therefore, statement (C) is the correct characterization of the data.
Correct Option: (C)

Question

Consider the function $f$. The table gives values of $\log_{3}(f(x))$ for selected values of $x$. Which of the following is a graph of $y = f(x)$ ?

(A)

(B)

(C)

(D)

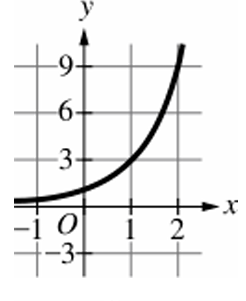
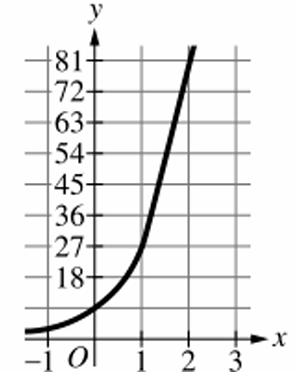
▶️ Answer/Explanation

Detailed solution

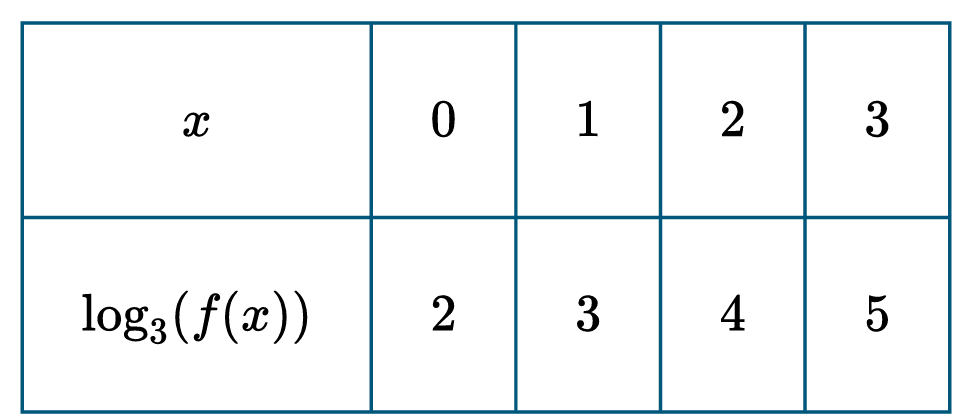
From the table, the linear relationship is $\log_{3}(f(x)) = x + 2$.
Convert this to exponential form: $f(x) = 3^{x+2}$.
Calculate the y-intercept by setting $x = 0$: $f(0) = 3^{0+2} = 9$.
Calculate the value at $x = 1$: $f(1) = 3^{1+2} = 27$.
Calculate the value at $x = 2$: $f(2) = 3^{2+2} = 81$.
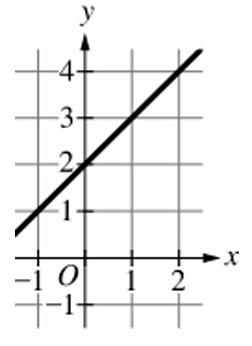
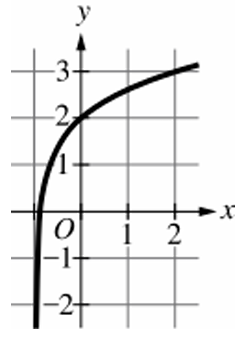
The graph must be exponential and pass through points $(0, 9)$ and $(1, 27)$.
Therefore, the correct choice is (D).

AP Precalculus -2.2 Linear and Exponential Change- MCQ Exam Style Questions - Effective Fall 2023